Применение преобразования Фурье в задаче фрактального кодирования изображений

Фрактальное кодирование является одним из наиболее перспективных на сегодняшний день методов сжатия изображений с потерями.

Рождение фрактальной геометрии обычно связывают с выходом в 1977 году книги Б. Мандельброта "Фрактальная геометрия природы". В конце 80х, начале 90-х годов М. Барнсли находит алгоритм построения по изображению его фрактального пред-ставления[1]. В 1992 году был опубликован первый практический алгоритм фрактального кодирования.

Фрактальное кодирование отличается высокой степенью сжатия и высокой скоростью восстановления изображения. Степень сжатия данного алгоритма сравнима с известными методами кодирования (например, JPEG [4]) , а скорость восстановления гораздо выше. Математическое описание изображения, являющееся результатом фрактального кодирования, позволяет восстанавливать изображение любого размера без значительных масштабных искажений, свойственных другим методам. Исходя из этого, фрактальное кодирование является очень перспективным для компьютерных мультимедиа– приложений и цифрового видео.

Основным недостатком метода является большая вычислительная сложность этапа кодирования изображения. Методы повышения скорости фрактального кодирования можно разделить на два класса: - методы ускорения вычислений без потери качества по сравнению с оригинальным алгоритмом, - приближённые методы вычисления.

Примером первого класса могут служить пирамидальные методы фрактального кодирования [3]. Однако, существующие методы повышения скорости сжатия не позволяют конкурировать фрактальному кодированию с другими широко используемыми методами.

Преобразование Фурье (кодирование изображений, спектральный анализ, методы фильтрации и т.д.) является мощным инструментом для работы с изображениями на сегодняшний день. Разработано множество алгоритмов для быстрого преобразования Фурье (БПФ), существует также и аппаратная реализация этого алгоритма.

Применение преобразования Фурье во фрактальном кодировании позволяет перевести задачу в плоскость спектрального анализа.

В работе описываются два метода ускорения операции фрактального кодирования различных классов:

• -    алгоритм с использованием быстрого вычисления свёртки спектральным методом [5],

• -   алгоритм спектральной оценки.

1. Классическая схема фрактального кодирования изображений

Опишем классическую схему фрактального кодирования.

Под изображением будем понимать двухмерный прямоугольный массив точек (отсчетов):

I = i(x, y), 0 < x < N, 0 < y < M, где (N, M) – размер изображения.

Пусть изображение I разбито на прямоугольные непересекающиеся области, называемые доменами :

Суть фрактального сжатия состоит в следующем. Для каждого домена производится поиск сжимающего аффинного преобразования области изображения, наилучшим образом аппроксимирующего данный домен. Параметры этого преобразования сохраняются для последующего восстановления до-

мена.

Для поиска аффинных преобразований на изображении выделяются ранговые области – прямоугольные области, покрывающие всё изображение: b

R = {Ri.. Rb}, U Ri = I ■ i=1

Для того чтобы аффинное отображение ранговой

области на домен было сжимающим, линейные раз-

меры ранговой области должны превышать размеры домена (обычно в 2 раза).

~

Линейная аппроксимация D домена D ранговой

областью R имеет вид[2]:

d ⁽ i , ^j ) = c 0 + c 1 ■ ~ ^{( i} , ^{j ) +} c 2 ■ i ⁺ c 3 ■ ^j , 0 <  i <  N ,0 <  j <  M ,

E=c mine D - DV c0 ,c1 ,c2 ,c3

где N, M – размеры домена, r~ - ранговая область, уменьшенная до разме-

ров домена,

E – ошибка аппроксимации.

На практике используется более простой вид ап-

проксимации :

d ( i , j ) = a ■ ~ ( i , j ) + b

В этом случае коэффициенты преобразования, а также ошибка аппроксимации имеют вид:

N ■ M ■

a =

>D , R^ - )j~,1( ■ ) D ,1(

N ■ M ■ RR, ~ - Ri/²

b = —¹-- ( D ,1 - a ■ \j~,1(

N ■ M ^v '    /

E = a ( a ■ ^ R , R^ + 2 ( b ■ ^R ,1^ - ^D , R^ )) + + b ( b ■ N ■ M - 2 ■ Du ,1 ) + ) D , D (,

где

M - 1 N - 1

) D1 = I I d ( m , n ), m = 0 n = 0

, M - 1 N - 1

)D,R^ = I Id(m,n)■ ~(m,n) - корреляция межДУ m=0 n=0

доменом и ранговой областью.

Аналогичные выражения существуют также и для общего случая.

Далее для каждого домена производится поиск наилучшей ранговой области, аппроксимирующей домен:

R k = m i n E ( D , R i )                                       (5)

Совокупность сжимающих преобразований для всех доменов образует аффинный коллаж изображения. Параметры преобразований аффинного коллажа являются кодом изображения.

Алгоритм восстановление изображения:

Шаг 1. Создается произвольное изображение (шум, константа) размеры которого не обязательно должны совпадать с исходными.

Шаг 2. Формируется второе изображение, являющееся результатом отображения аффинного коллажа.

Шаг 3. Изображения меняются местами.

Шаг 4. Процесс продолжается до момента, когда изображения перестают отличаться друг от друга. На практике необходимо всего 4-5 итераций.

Замечание:

В работе [6] показано, что при восстановлении можно обходиться одним изображение, что экономит ресурсы и увеличивает скорость сходимости. При этом отображение аффинного коллажа происходит на это же изображение.

• 2 . Алгоритм фрактального кодирования с использованием быстрого вычисления свёртки

Основная идея использования алгоритма быстрой свёртки основана на том, что ранговые области на изображении в общем случае перекрываются. Следовательно, эту информацию можно использовать для ускорения вычислений.

Рассмотрим вычисление коэффициентов линейного преобразования (3). Данная операция осуществляется для каждой пары (домен, ранговая область).

Наиболее вычислительно трудным является расчет корреляции домена и ранговой области . Другие составляющие , , , не зависят от соотношения домена и ранговой области и могут быть вычислены один раз.

Рассмотрим следующую схему фрактального кодирования:

Пусть Y - уменьшенное (в два раза) изображение. Ранговые области на этом изображении будут иметь размеры домена. Каждой точке этого изображения будет соответствовать своя ранговая область. При этом ранговые области для крайних точек циклически продолжаются на противоположный край изображения.

Тогда для каждого домена D вычисление корреляции с ранговыми областями сводится к вычислению циклической свертки между доменом D и изображением Y .

Существует алгоритм быстрого вычисления циклической свёртки двух изображений спектральным методом[7]. Для этого необходимо получить спектры изображений, выполнив быстрое преобразование Фурье (БПФ). Далее, необходимо перемножить спектры и выполнить обратное преобразование (ОБПФ).

Схема алгоритма:

Шаг 1 . Предварительные вычисления:

• -   создание уменьшенного изображения Y,

• -    вычисление спектра У ,

• -   вычисление параметров ранговых областей

• < R,1>, .

Шаг 2 . Кодирование каждого домена:

• -    вычисление параметров   домена ,

.

• -    вычисление расширенного нулями до размеров изображения У спектра домена D .

• -    перемножение спектров У и D .

• -    обратное БПФ даёт изображение, элемен-

• тами которого являются корреляции между доменом и соответствующей ранговой областью.

• -    расчет параметров преобразований по формуле (3,4) и выбор наилучшего преобразования.

Шаг 3 . Сохранение параметров аффинного коллажа.

Сравним количество операций кодирования с классической схемой.

Пусть размер исходного изображения N x N. Размер домена M x M. Количество ранговых областей

N ²

.

Тогда количество операций необходимое для вычисления прямой свёртки - 1 ■ _N 2 ■ м 2 .

Если размеры изображения и домена являются степенями двойки, то количество операций вычисления быстрой свёртки составляет:

• -    Вычисление БПФ домена - 10 ■ м ² ■ log₂ м

• -    Перемножение спектров -3 N ₄

• -    Вычисление ОБПФ 52 n ² . (i_og₂ N - 1)

Общее количество операций составляет

N ² ■ (5/ ■ (log 2 N - 1) + % + 10 ■ M ² ■ log 2 M )

• 2             4 _N 2

• 3 . Алгоритм спектральной оценки

В таблице 1 приведено количество операций вычисления свёрток на каждую точку изображения при N=256.

Таблица 1

Размер домена	Прямая свёртка	Быстрая свёртка	Отношение
M=4	8	18,25	0,44
M=8	32	18,253	1,75
M=16	128	18,41	6,95
M=32	512	19,03	26,91

При больших размерах домена алгоритм дает значительный выигрыш в скорости. Разработанные в настоящее время алгоритмы БПФ различных длин позволяют с большой скоростью

Различные алгоритмы совмещения БПФ позволяют еще больше повысить скорость вычисления свёртки.

Насколько видно из таблицы 1 метод дает хорошие результаты при больших размерах домена Данный алгоритм остается при этом алгоритмом “полного” перебора ранговых областей.

Основным недостатком классического алгоритма фрактального кодирования является необходимость “полного” перебора ранговых областей для поиска наилучшей аппроксимации. Один из способов повышения быстродействия алгоритма заключается в быстрой оценке ошибки аппроксимации с целью выбора лучших (отсеивания худших) ранговых областей.

Рассмотрим процедуру поиска наилучшей ранговой области:

R k = min E ( d , R i ) R

^d '( t 1 , t 2 ) = A 00 ⁺

+ to to ZZ aj i=1 j=1 - cosl ' 2mt 1' . M > 1 - cosl ^ 2njt 2 < N + toto ZZ bj i=1 j=1 ■ sin[ 2nit 1 ] M J - sin^ 2njt2 ) NJ + (11) + toto ZZ cij i=1 j=1 cosl ' 2nt 1 ^ MJ 1 ■ sin ' 2njt 2' NJ 1+ + toto ZZ dij i=1 j=1 ■ sm^ 2rn"t 1 ^ MJ cosl " 2njt2 ' N ) где

A ₀₀, a_ij , b_ij , c_ij , d_ij - коэффициенты ряда Фурье.

При этом, в силу ортогональности базисных функций дискретного преобразования Фурье коэффициент корреляции может быть представлен в виде:

D , R

1           to to

D ( D ) ■ D ( ~ ) i ^Z 0 j = 0 ^Z j a c ' a ij +

~~

⁺ b j ' b ij ⁺ + • c j ' c ij ⁺ d ij ' d ij ]’

Очевидно, что качество аппроксимации домена ранговой областью не зависит от средних значений яркости в них. Следовательно, положим:

(R,1) = 0, ( D ,1) = 0

При этом соотношения (3, 4) преобразуются к

следующему виду::

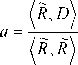
b = 0,

E ( R , D ) =< D , D >+ a ² ■ < R , R\ - 2 ■ a ■ RR , D =

где

r =

(D , D ) -

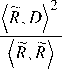
¹ - r ² )

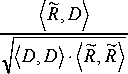
коэффициент корреляции

между доменом и ранговой областью.

Следовательно критерий поиска наилучшей ранговой области (6) имеет вид:

^R k = max r ^{( D} , R i )                           (9)

R

В случае ненулевых средних значений коэффи-

циент корреляции:

r ( D , R ) =

(R , D - ( D , D ■ RR , R)

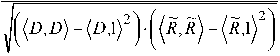
Представим домен в виде непрерывной функции d ( 1 1 , 1 2 ) , определенной на прямоугольной области с размерами (N,M) и центром в точке (0, 0).

Разложим функцию d ( t 1 , t ₂ ) в двумерный ряд

где

D(d) = ^d, d^ - Du,12 - дисперсия по домену, a~ j ,b~ j ,c~ j , d~ j - коэффициенты разложения Фурье ранговой области.

Оценку коэффициента корреляции (12) будем производить по некоторому множеству индексов коэффициентов Q :

~~       1             ~ r (D-R) D (D >D (~) (j:i;• " bj bj+(13)

⁺ c ij -~Су ⁺ d ij -dy ]•

В качестве множества коэффициентов возьмем низкочастотные составляющие ряда Фурье:

Q = {(i, j)| i+ j < P} p=2 .                     ~~

Часть коэффициентов a ^~ _ij , b_ij , c ^~ _ij , d_ij тождественно нулевая. Следовательно, количество коэффициентов уменьшается до 12.

Деление на дисперсию можно производить один раз при расчете коэффициентов разложения Фурье ранговых областей. Таким образом, количество операций по оценке домена составляет 23 и не зависит от размера домена.

Количество операций, необходимых для вычисления ошибки аппроксимации по формуле (4) составляет:

K = 23 + 2 - M ²,                             (15)

где

M - размер домена.

В таблице 2 показано количество операций для вычисления ошибки аппроксимации и оценки коэффициента корреляции для различных размеров доменов.

Фурье:

Таблица 2
Размер домена	Ошибка аппроксимации	Оценка корреляции	Отношении
M=4	55	23	2,39
M=8	151	23	6,57
M=16	535	23	23,26
M=32	2071	23	90,04

Схема алгоритма:

Шаг 1 . Предварительные вычисления

• -    Вычисление для каждой ранговой области локальных параметров и нормированных коэффициентов ряда Фурье.

Шаг 2 . Для каждого домена

• -    Вычисление локальных параметров и коэффициентов ряда Фурье.

• -    Выбор небольшого числа K лучших ранговых областей по критерию максимума модуля корреляции (13).

• -    Для К ранговых областей выбор наилучшей аппроксимации по критерию максимума модуля коэффициента корреляции (9).

Шаг 3 . Сохранение параметров аффинного коллажа.

Проведенные экспериментальные исследования показали следующее:

Количество лучших ранговых областей К необходимо выбирать в размере 1-3% от общего числа ранговых областей. При этом общая погрешность кодирования практически не превосходит погрешности классического метода.

При этом погрешность восстановления отдельных изображений была ниже погрешности классического метода. Этот факт объясняется тем, что итеративный процесс восстановления лучше восстанавливает низкочастотные составляющие изображения, на основе которых и происходит оценка ранговых областей.

Небольшая потеря качества данного метода фрактального кодирования может быть восполнена за счет увеличения количества просматриваемых ранговых областей.

Применение коэффициентов Фурье позволяет также значительно расширить количество ранговых областей практически без дополнительных операций. Это возможно благодаря тому, что такие преобразования спектра Фурье как поворот или отражение легко пересчитываются.

Заключение

В работе рассмотрены методы применения преобразования Фурье в задаче фрактального сжатия изображений. Данные методы позволяют значительно увеличить скорость фрактального кодирования изображений. Предложен новый алгоритм “неполного” перебора на основе коэффициентов ряда Фурье. Этот алгоритм “с потерей качества” по погрешности восстановления не уступает классическому алгоритму, а по скорости значительно превосходит его. Получено существенное увеличение скорости фрактального кодирования при больших коэффициентах сжатия.