Применение примеров решений задач вибродиагностики при изучении алгоритмов цифровой обработки сигналов

1При решении многих технических задач, связанных с обработкой реальных данных, активно применяются современные компьютерные средства и технологии, которые реализуют различные методы и алгоритмы цифровой обработки сигналов. Поэтому при подготовке специалистов в области компьютерной техники и программирования, одной из сфер профессиональной деятельности которых является разработка и эксплуатация подобных устройств и систем, требуется существенное внимание уделять данной предметной обла-

сти. Учебные программы предметов, связанных с вопросами цифровой обработки сигналов (ЦОС), как правило, включают такие разделы, как спектральный анализ, цифровая фильтрация, численное интегрирование, сглаживание данных, вейвлет-анализ, которые базируются на соответствующих разделах математики. Однако просто формальное изложение данного материала в ходе учебного процесса вызывает у студентов некоторое непонимание его практической применимости. Поэтому для лучшего понимания и усвоения вопросов цифровой обработки сигналов и данных весьма полезно теоретические сведе-

HAVKO____________

Ж ГРАДА ния сопровождать реальными примерами их использования при решении конкретных прикладных задач.

Практически все основные методы и алгоритмы ЦОС используются при решении задач вибрационного контроля, мониторинга и диагностики. При этом приходится обеспечивать достижение высокой точности определения параметров вибросигналов при наличии различных возмущающих факторов и помех, а также реализовывать различные специальные ⁵⁰ методы выделения информативно значимых признаков.

В результате выполнения работ научно-исследовательской лабораторией вибро-диагностических систем Белорусского государственного университета информатики и радиоэлектроники получен большой объем экспериментальных данных, разработаны алгоритмы и программные средства, которые позволяют осуществить наглядную демонстрацию применения алгоритмов ЦОС.

Вибрационные сигналы, полученные при исследовании работы механизмов и агре-

№ 1 (3) январь-март 2013

гатов с вращательным движением (рис. 1), представляют собой композицию периодической p ( nt_d ) и шумоподобной s ( nt_d ) составляющих:

x ⁽ nt d ) = Р ( nt d ) + ^s ( nt d ) =

L

= Z A m cos [ ^{2 n} k m f o nt d - ^Ф m ] + ^{S (} nt d ), m = 1

где n – номер дискретного отсчета, n = 0, 1, 2, …; t _d – интервал дискретизации; f _о – частота вращения приводного вала (оборотная частота); k_m – кратность т -й гармоники, включенной в периодическую составляющую, относительно f_o ; A m , f m ,, ф _m - амплитуда, частота, начальная фаза т -й гармоники, f_m = k_mf _о; L – число гармоник в периодической составляющей вибросигнала.

Кратность гармоник, входящих в состав периодической составляющей вибросигнала, определяется с учетом параметров подшипников, зубчатых передач, схемы редуктора контролируемого узла и его других

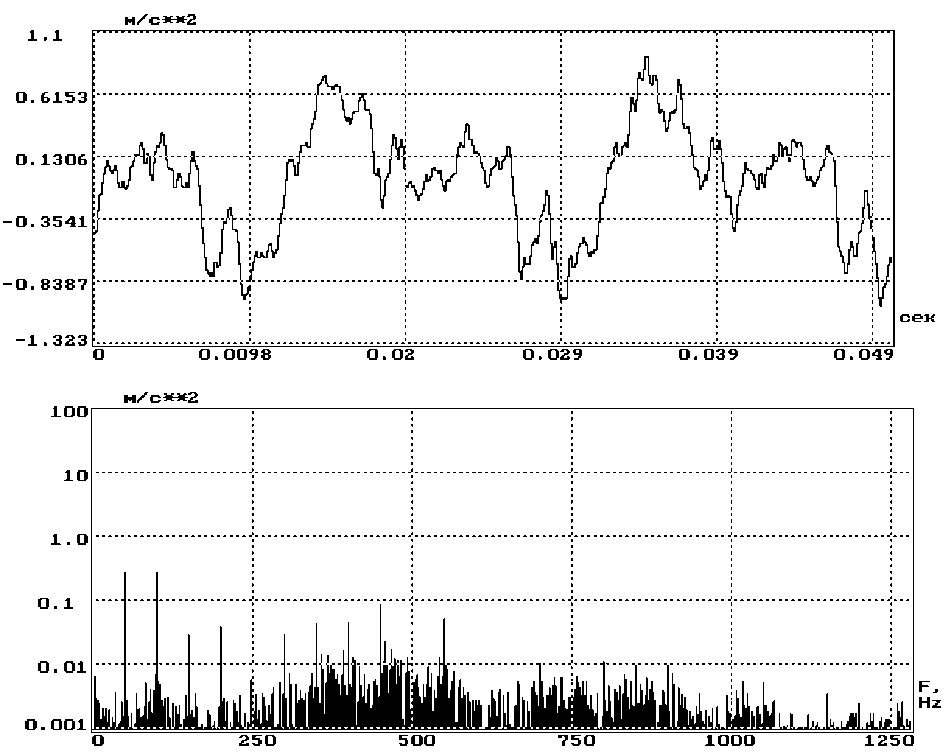
Рис. 1. Временная реализация и амплитудный спектр вибрационного сигнала

конструктивных особенностей. Если точно известна частота f о , то амплитуда и начальная фаза т -й гармоники легко вычисляются с помощью дискретного преобразования Фурье, причем количество дискретных точек преобразования выбирается таким, чтобы интервал анализа был кратным (в рамках возможностей интервала дискретизации) периоду f_т .

Однако на практике для контроля вибрации часто используют приборы, в которых отсутствует измерительный канал для фазо- вого датчика, применяемого для определения частоты вращения и фазовых сдвигов оборотных составляющих вибрации. Традиционный же спектральный анализ позволяет точно вычислить первую и другие оборотные частоты только в том случае, если они кратны фундаментальной частоте спектрального анализа. При проведении исследований вибрационного состояния реальных объектов такой крат- ности удается достигнуть далеко не всегда. Следствие этого - размывание оборотной частотной составляющей по соседним спектральным линиям и проблемы с определением её значения.

Теоретические и экспериментальные исследования [1-3] показали, что частоту и амплитуду оборотной составляющей можно определить с хорошей точностью, используя следующие выражения:

f O =А f

⁽¹ + ^{1 )-}

A i

A i + A + 1

A = Ai" Ai+1

fo A + A^ Д

Sin n

• < A i ⁺ A i + 1 >

где Δ f - частотное разрешение спектрального анализа; A _{i +} , A_{i + 1} - амплитуды спектральных составляющих, являющихся ближайшими в меньшую и большую сторону относительно оборотной частоты.

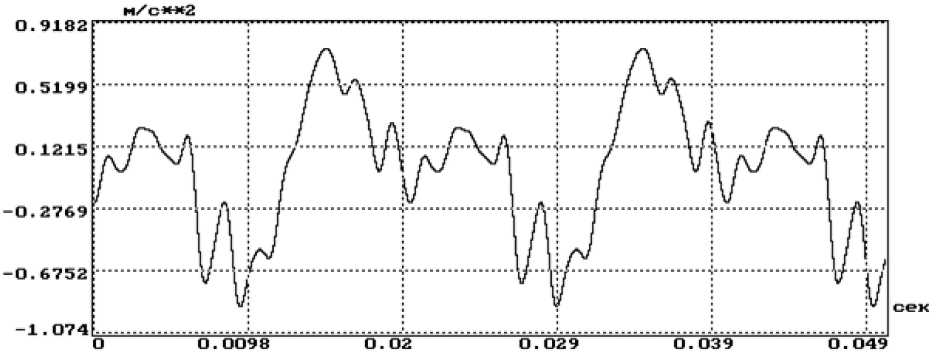
Когда частота f _о найдена, периодическая составляющая сигнала p ( nt_d ) вычисляется по формуле левого слагаемого выражения (1), а шумоподобная составляющая находится как

• ^{5 (} nt d ) = x ⁽ nt d ) - p ⁽ nt d ).

Далее выполняется раздельная обработка выделенных составляющих и определяются их параметры.

В качестве примера на рис. 2 представлены результаты разложения вибрационного сигнала, изображенного на рис. 1, на периодическую и шумоподобную составляющие.

Вычисление амплитудного спектра сигнала осуществляется с помощью алгоритмов дискретного и быстрого преобразования Фурье. Для отображения исходных временных реализаций сигналов и их спектров в ходе лабораторных работ студентами разрабатываются программы, реализующие данные функции. При этом существенное влияние уделяется вопросам представления шкал. Для отображения амплитудного спектра используется как линейная, так и логарифмическая шкала. Последняя шкала позволяет детально рассмотреть малые (тысячные и сотые) и большие (десятки и сотни) значения отображаемых данных.

Исходные вибрационные сигналы обычно представлены в единицах ускорения. Переход к единицам виброскорости и виброперемещения, в которых обычно осуществляется нормирование допустимых уровней вибрации, производится с помощью интегрирования. Интегрирование выполняется во временной или в частотной областях. Вычисление параметров вибрации механизмов осуществляется в определенных частотных полосах (например, 10-1000 Гц). Для выделения сигналов в этих полосах применяется цифровая фильтрация, реализуемая различными способами [2].

На вычисление амплитудного спектра сигнала сильное искажающее воздействие, проявляющееся в «замазывании» низкочастотной области, оказывают его медленные дрейфы (рис. 3), которые могут возникать при быстром изменении температуры контролируемого объекта, температуры первичного датчика или изменении питающих напряжений согласующих усилителей.

Для выявления характера изменения зашумленного, но вместе с тем достаточно медленно изменяющегося сигнала на каком-то временном отрезке, можно найти описание этого изменения в виде алгебраического многочлена, причем для практического применения можно ограничиться первой или второй степенью этого многочлена.

Так как многочлен должен описывать дрейф на всем интервале анализа, то он может быть найден как среднеквадратическое приближение в виде полинома:

P n ( x ) = c ₀ + c ₁ x + c ₂ x ² + ... + c_nxⁿ .

ГРАДА

0.02

0.029

0.039

0.049

м/с**2

0.9182

0.5199

0-1315

-0.2769

-0.6752

сек

0.0098

-1 . O74L О

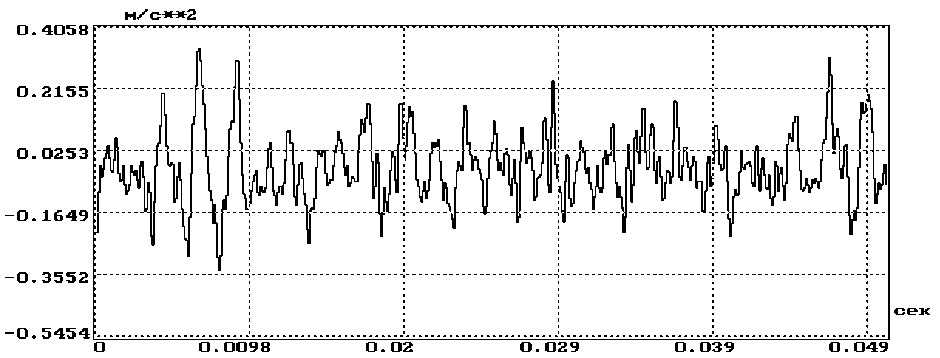
Рис. 2. Периодическая и шумоподобная составляющие вибрационного сигнала

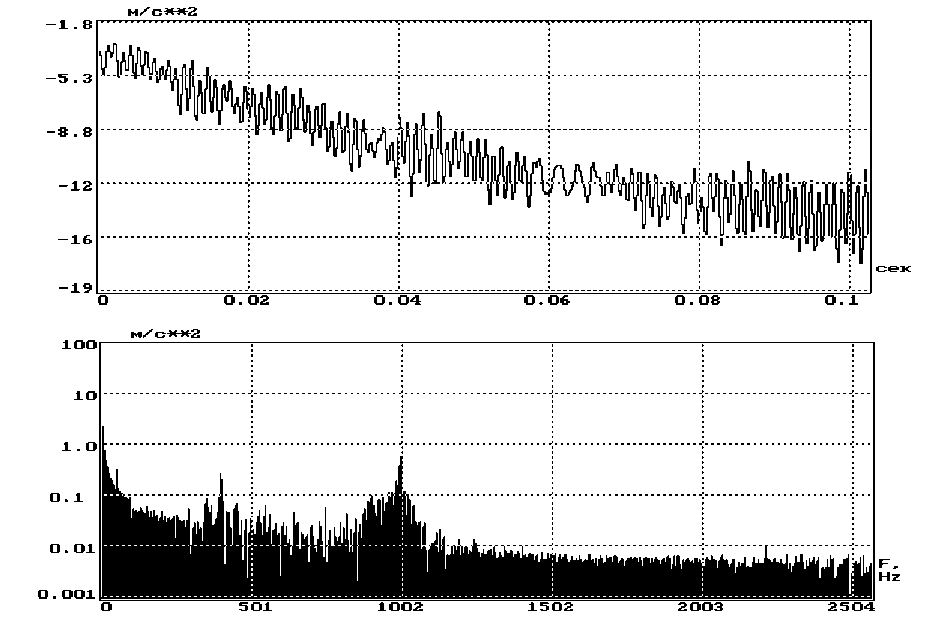
Рис. 3. Форма и амплитудный спектр вибросигнала при наличии дрейфа

Значения коэффициентов многочлена наилучшего приближения находятся путем решения системы уравнений:

c 0 5 00	+ C 1 5 10	+	c 2 s 20	+ .	■+ c n5n 0 =	= r 0 ;
c 0 5 01	+ C 1 5 11	+	c 2 s 21	+	• + Cn5n1 =	r 1;
1 c 0 5 0 .	+ C 1 5 1 й	+	c 2 s 2 n	+	•• + Cn5nn	= r n .

Для функции f ( x ), представленной в дискретном виде, со значениями аргумента от 0 до N – 1:

N - 1

S„ = У X i ⁺ j

ij                          ;

x = 0

N - ¹

r = E f ( x ) • ^{X .}

x = 0

На практике для описания низкочастотного дрейфа целесообразно применять полиномы первой или второй степени. Для полинома первой степени система уравнений

имеет вид

<

c 0 s 00

_ c 0 ⁵ 01

⁺ c l ⁵ _W

^{+ c} 1 ⁵ 11

= ^r 0 ;

= r r

Решая эту систему, получим:

c 0 = (

r 1 s 10

^^^^^^^B

r 0 ⁵ 11 )/(

s 01 s 10

^^^^^^^B

⁵ 00 ⁵ 11 ) ^;

c 1 =⁽

r 0 s 01

^^^^^^^B

r 1 ⁵ 00 )/(

s 01 s 10

^^^^^^^B

Для полинома второй степени система принимает вид c0500 + c1510 + c2 5 20 = r0;

* c 0 ⁵ 01 ⁺ c 1 ⁵ 11 ⁺ c 2 ⁵ 21 = ^r 1 ;

C ₀ 5 02 + C 1 5 ₁₂ + C 2 5 22 = Г 2 .

В этой системе значения коэффициентов s определяются выражениями:

N - 1

5 00 = E i = n ;

x = 0

N - 1

5 10 = 5 01 = E X = N ( N - 1)/2;

x = 0

5 11 = 5 20 = 5 02 = E X ² = N ( N - 1)(2 N - 1)/6;

x = 0

5 12 = 5 21 = E X ³ = N ²( N - 1) 2/ 6;

x = 0

N - 1

5 ₂₂ = E X 4 = |_ N ( N - 1)(2 N - 1)(3( N - 1)² + x = 0

+ 3( N -1) -1) ] /30, а коэффициенты r рассчитываются по формулам:

N - 1

г = E f ^{( X} )

x = 0

N - 1

r = E f ^{( X} ) ■ ^X ;

x = 0

N - 1

r 2 = E f ^{( X} ) ■ ^{X 2}.

x = 0

Применив метод определителей для решения системы, можно получить коэффициенты для полинома второй степени:

c 0 = D0ID ;

C 1 = D 1 ID ;

C 2 = D 2/ D , где

D = k ₀ k ₂ k 4 + 2 k 1 k ₂ k ₃ - k 1 ² k 4 - k ₀ k ₃ ² - k ₂³;

D ₀ = r ₀ k ₂ k ₄ + k ₃ ( r ₂ k 1 + r 1 k ₂) - r 1 k 1 k ₄ - r ₀ k ₃ ² - r ₂ k 2 ;

D 1 = r 1 k ₀ k ₄ + k ₂ ( r ₀ k ₂ + r ₂ k 1 ) - r ₂ k ₀ k ₃ - r 1 k ₂ ² - r ₀ k 1 k ₄;

D ₂ = k ₂( r 1 k 1 + r ₂ k ₀) + r ₀ k 1 k ₃ - r ₀ k 2 - r ₂ k 1 ² - r 1 k ₀ k ₃;

^k 0 = ⁵ 00 ; ^k 1 = ⁵ 01 = ⁵ 10 ;

^k 2 = ⁵ 02 = ⁵ 11 = ⁵ 20 ^;

^k 3 — ⁵ 12 — ⁵ 21 ^{; k} 4 — ⁵ 22 .

Путем вычитания значений полинома с вычисленными коэффициентами из исходного сигнала производится удаление медленного дрейфа, что позволяет демаскировать низкочастотную область (рис. 4) [4].

В ходе развития вибрационных процессов могут возникать различные аномальные явления, связанные с зарождением и развитием дефектов технических объектов или с какими-то другими причинами. Для оценки динамики изменения вибросигнала в той или иной частотной зоне используется вейвлет-анализ, с настройкой центральной частоты вейвлета на определенное значение. Также решаются задачи сглаживания данных [5].