Применение принципа максимума в задаче управления рекламными расходами

Для разработки фирмой грамотной рекламной стратегии по оптимизации затрат на рекламу в плановом периоде необходимо знать, каким образом реклама воздействует на потенциальных покупателей. При этом нужно учесть, что между однократным рекламным сообщением и совершением некоторыми потребителями покупок образуется лаг запаздывания. Это может объясняться различными причинами. Например, если ознакомление с информацией о товаре произошло не напрямую, а через третьи лица, которые в свою очередь таким же образом могли познакомиться с продуктом спустя промежуток времени после запуска рекламного сообщения. Также после ознакомления с рекламным объявлением потребителю зачастую необходимо время для того, чтобы обдумать необходимость приобретения прорекламированного товара, а после принятия решения о покупке — время до ее совершения.

Для построения модели также важно учесть влияние совокупности других факторов, стимулирующих потребителей повторно приобретать продукт данной фирмы, например, его качество, сформировавшаяся привычка и др. При этом влияние ранее совершенной покупки на текущую также может со временем возрастать на начальном этапе до определенного момента, после чего ослабевает, и влияние в большей степени оказывают более поздние покупки.

На сегодняшний день существуют различные подходы к управлению рекламными расходами. Выделяя подходы, основанные на математическом моделировании, можно отметить вероятностные модели, учитывающие охват, частоту показа [5]; регрессионные эконометрические модели [2]; динамические дискретные и непрерывные модели [1, 3]. Однако существующие непрерывные модели управления рекламными расходами предполагают учет только мгновенной реакции от воздействия. В настоящей работе предлагается развитие динамической непрерывной модели управления рекламными расходами, предложенной в работах [7, 8]. При этом в модели учитываются распределенные эффекты воздействия рекламы и предыдущих продаж фирмы.

Постановка проблемы

Обозначим через y(t) и u(t) выручку фирмы от продаж — численное выражение реакции потребителя и величину рекламных расходов в момент времени t соответственно. Если предположить, что рассматриваемая фирма занята в сфере предоставления услуг и основные ее затраты направлены на маркетинговые мероприятия, то функционал, представляющий собой суммарную прибыль П(T) на планируемом периоде t □ [0; T], можно определить в виде

T

П ^{( т} ) = / ⁽ У ⁽ t ) - u ⁽ t )) ^ max,            (1)

где функция выручки У ( t ) имеет вид

У ⁽ t ) = F ⁽ v ⁽ t ), w ⁽ t ⁾⁾-                 (2)

За v ( t ) обозначим накопленный эффект рекламы, за w ( t ) — накопленный эффект предыдущих продаж, учитываемые на интервале от начального момента планирования до текущего момента времени

t

^{v (} t ) = f G u ^{( т} ) u ^{( т} ) d ^T ,

t w (t) = f Gy (т) y (t ) dT, v (0) = 0, w (0) = 0,

где G_u ( t ) , G y ( т ) — функции, определяющиеся на интервале т е [0; t ] , где т — лаг запаздывания, характер воздействия рекламных затрат и предыдущих продаж соответственно.

Как правило, рекламные расходы, планируемые фирмой на определенный период, практически всегда имеют пороговое значение:

0 <  u ( t ) <  b , t е [0; T ]. (4)

Задача максимизации прибыли (1) при условии (2) с учетом интегральных уравнений (3) и ограничения на рекламные расходы (4) дает задачу динамической оптимизации.

Основные результаты

В силу вышеуказанных причин, из-за которых наблюдается запаздывание реакции потребителей, можно предположить, что заинтересованность населения в рекламируемом продукте со временем возрастает, начиная с момента выхода рекламного сообщения, до какого-то максимального значения. После этого отдача от рекламного воздействия убывает в связи с тем, что часть потенциальных покупателей, информированная о товаре через рекламу фирмы, забывает об этом или покидает рынок по каким-либо другим причинам.

Что касается эффекта воздействия предыдущих продаж, то влияние ранее совершенной покупки на текущую также может со временем возрастать на начальном этапе до определенного момента, после чего ослабевает, и воздействие на потребителя в большей степени оказывают более поздние покупки. Функции G_u ( т ) , G y ( т ) в этих случаях принимают вид, изображенный на рисунке 1.

Для практического представления зависимости, изображенной на графике (рис. 1), функции G_u ( т ) , G y ( т ) могут определяться следующим образом:

G_u ( т ) = a_ue^b - ^{т +} c u ^т ,                  (5)

uu

G_y ( т ) = a_ye b^{т +} c y ^т .               (6)

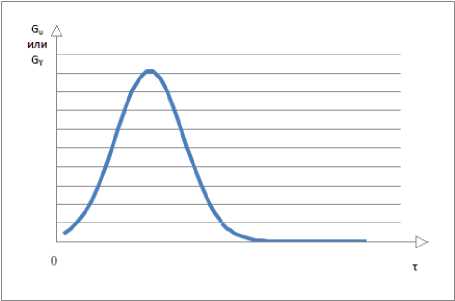
Рис. 1. Общий вид графиков функций G_u ( т ) , G y ( т ) в соответствии с (5) и (6)

Возможен и несколько иной характер реакции потребителя: убывание отдачи от рекламного воздействия может иметь монотонный характер, т. е. реакция на рекламу принимает максимальное значение практически сразу после выхода рекламного сообщения и оказывает меньшее влияние на последующие продажи. Монотонно убывающим может также оказаться и влияние предыдущих продаж, когда воздействие совокупности других факторов не оказывает настолько сильного воздействия на потребителя, чтобы заставить его приобретать товар в большем объеме по сравнению с предыдущими покупками.

В этом случае G u ( т ) , G y ( т ) принимают вид, изображенный на рисунке 2. При этом функции могут определяться следующим образом:

G_u ( т ) = a_ue^? u ^T ,                 (7)

uu

G y ( т ) = a y C^b^^T .               (8)

t

x(t) = J f (t, x(5), U(5))ds

введем также функции xi(t), x2(t), xg(t), та кие что

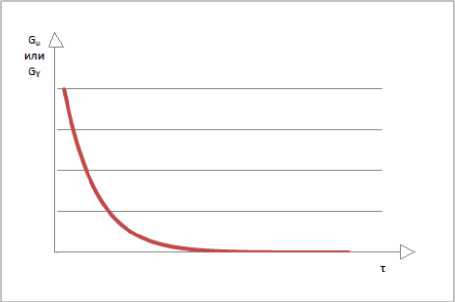
Рис. 2. Общий вид графиков функций G u ( т ) , G y ( т ) в соответствии с (7) и (8)

x 1 ( t ) = v ( t ), x 2 ( t ) = w ( t ), x з ( t ) = П ( t ) . (12)

Из уравнений (10)—(12) составим следующую систему линейных интегральных уравнений типа Вольтерра первого рода:

x ( t ) =

' ^x 1 ( t )' x , ( t ) I. ^X 3 < t ) )

t

= J

^ G U ⁽ t ^{- 5} )) ^{U ( 5} )

^G y ⁽ t ^{- 5} ) F ⁽ x 1 ^{( 5} ), x 2 ^{( 5} ))

⁰ ( F ( x i ( 5 ), x 2 < 5 )) - U ( 5 )

\

d5 ,

V

x i (0) = 0, x 2 (0), x 3 (0) = 0.                   (13)

В соответствии с (13) функционал (1) можно представить в виде x3 (t) ^ max или -x3 (t) ^ min.    (14)

Отметим также, что параметры a_u , b _u , c _u , a_y , b_y , c_y подбираются эконометрически на основе параметров α и β множественной регрессии:

У(t) = а У(t - тд.) + ^u(t - тд.), тд. = 0,1, 2,..., где тд. — дискретные значения лагов запаздывания. При этом функции Gu (т), Gy (т) определяются как результат точечной аппроксимации по значениям векторов α и β соответственно.

Введем новую переменную 5 = t - т и перепишем (3) следующим образом:

v (t) = jGu (t - 5 ) U ( 5 ) ds, w (t) = jGy (t - s) y (5) ds.

Определим суммарную прибыль на текущий момент времени:

t

П ( t ) = J ( y ( t ) — u ( t )).               (11)

Для сведения интегральных уравнений (10), (11) к системе уравнений типа Вольтерра вида

Таким образом, преобразованная задача оптимального управления представлена уравнениями (4), (13), (14).

Поставленная задача (4), (13), (14) представляет собой задачу оптимального управления с интегральными уравнениями. Применим для данной задачи принцип максимума Понтрягина, сформулированный для данного класса задач в работе [4].

Введем модифицированную функцию Гамильтона-Понтрягина

H ( 5 , x , U ) = y /( 5 ) f ( 5 , 5 , x , U ) +

T

+ J v (.t ) f t ( t , 5 , x , U ) dt

s и концевую функцию Лагранжа

l ( x (0), x(T )) =

- x ₃ ( T ) + b 1 x 1 (0) + b ₂ x ₂ (0) + b ₃ x ₃ (0),

где ^ ( 5 ) = ( ^ 1 ( 5 ) ^ 2 ( 5 ) V 3 ( 5 )) — ^вектор функций сопряженных переменных, при этом

^ 1 ^{( 5} ) = H x 1 ^{( 5} , ^x , ^U ), у / ₂( 5 ) = H x ₂ ( 5 , x , U ),                  ⁽¹⁷⁾

у/3<5) = Hx3 (5,x,U), где d H (5, x, u )

Hx (5, x, u ) =----- a h (5, x, u)

Hx (5, x, u ) =-----

О X ₂

a h ( 5 , x , u )

Hx (5, x, u ) =----".

Согласно (15) определим функцию f ( t , x ( 5 ), u ( 5 )) при t = 5 , а также найдем ее частную производную по t :

Ц ⁽⁵ ) = ^ 1 ^{( 5} ) G u ⁽⁰⁾ - V 3 ^{( 5} ) ⁺

+ T ( V i ( t ) G „ ( t - 5 )) dt ,

и оптимальное управление находится из соот-

ношения

<

u ( 5 ) = b ,

u ( 5 ) = 0,

если ju ( 5 ) > 0, если ^ ( 5 ) <  0.

f G u (0) u ( 5 )

к

Выпишем условия, определяющие функции сопряженных переменных [4]:

f ^{( 5} , ⁵ , ^x , u ) = G y ⁽⁰⁾ F ^{( x} j ( ⁵ ), ^x 2 ^{( 5} )) , V F ^{( x} 1 ^{( 5} ), ^x 2 ^{( 5} )) ^- u ^{( 5} ) у

f G u t ⁽ t ^{- 5} ) ^{u ( 5} )

f t ⁽ t , ⁵ , ^x , и ) = G yt ⁽ t ^{- 5} ) F ^{( x} i ^{( 5} ), ^x 2 ^{( 5} )) , (19)

V о

где

f t ( t , 5 , x , u ) =

d f ( 5 , t , x , u )

dt

,

G u, ( t - 5 ) =

G y, ( t - 5 ) =

dG u ( t — 5 )

dt ’ dGy (t - 5)

■ условия трансверсальности:
	1(0, = бз^ет = в 1 , дx i (0) V (0) = d( x (0); x ( T )) = в , 2          д x 2(0)
	V (0) = д( x (0 >- x ( T» = А , 3          д x 3(0)        3 V ( T ) =_ d( x (0)1 x ( r )) = 0, ’ 1 '         д x i ( T ) V ( T ) = - д( x (0 >, x ( T )) = 0, ' 21 '         xx 2 (0) V ( T ) = - д( x (0) , x ( T » = 1. /3            ax 3(t )	(23)

dt

•

Преобразуем функцию Гамильтона-Понтрягина (15), подставив (18), (19):

^{H ( 5} , ^x , и ) = ( ^ ^{( 5} ) G u ^{(0) -} ^ з ^{( 5} ) +

T                                         (20)

+ j W t ) ^G ut ⁽ t ^{- 5} )) ^dt ) ^{u ( 5} )•

s

Так как функция Гамильтона-Понтрягина имеет линейный характер по переменной u ( 5 ) , то максимум функции достигается на границе ограничений управления, и имеет смысл рассмотреть множитель при переменной u ( 5 ) , который можно назвать функцией переключения управления. Функция переключения ц ( 5 ) определяет релейный характер управления, и на основе знака этой функции можно для фирмы рассчитать оптимальные вложения в рекламу. В нашем случае функция переключения определяется следующим образом:

■ дифференциальные уравнения сопряженных переменных исходя из (13), (17):

'< ^ 1 ^{( 5} ) = -V 1 ^{( 5} ) ^G y ^{(0) F} x_x ^{( x} i ^{( 5} ), ^x 2 ^{( 5} )) -

• -    ^F x , ^{( x} i ^{( 5} ), ^x 2 ^{( 5} )) -

• -    j ( V 1 ( t ) G y_t ( t - 5 ) F x _ ( x i ( 5 ), x 2 ( 5 ))) dt ,

• ³ 4 ^ 2 ⁽ 5 ) = ^- V 1 ⁽ 5 ) G y ^{(0) F} x ₂ ⁽ x i ⁽ 5 ), x 2 ⁽ 5 )) ^{-    (24)}

• ^{-    F} x ₂ ^{( x} i ^{( 5} ), ^x 2 ^{( 5} )) ^-

• T

• ^-    j ⁽ V 1 ⁽ t ) G y_t ⁽ t ^{- 5} ) ^F x ₂ ^{( x} i ^{( 5} ), ^x 2 ^{( 5)))dt} , ⁵

[ у / з ( 5 ) = 0.

Решение краевой задачи (23), (24) представляет из себя довольно сложную проблему, так как в общем случае система не имеет аналитического решения и требуется применение численных методов решения интегро-дифферен-

циальных уравнений. В частности, для задачи (4), (13), (14) можно использовать метод параметризации, расширенный на данный класс задач в работе [6].

Рассмотрим частные случаи модели (4), (13), (14), когда функция выручки F ( X i ( 5 ), x 2 ( 5 ))

линейна по переменным X i , x 2 -

Линейные модели оптимального управления рекламными расходами

Пусть в обоих случаях зависимость реакции потребителей на рекламное воздействие и предыдущие покупки представлена в линейной форме — выручка фирмы в текущий момент времени равна сумме накопленных эффектов воздействия рекламы и предыдущих продаж:

y ⁽ t ) ^- F ⁽ x ⁽ t ), ^x 2 ⁽ t )) ^- v ⁽ t ) + w ⁽ t ).      (25)

При этом с учетом известных значений

У 1 ( Т ) и у 2 (T ) из (23) система уравнений (24) принимает следующий вид:

V i ( 5 ) = - V i ( 5 ) G y (0) - 1 - T ( V i ( t ) G y t ( t - 5 )) dt ,

’ V 2 ( 5 ) = V 1 ( 5 ),                                     (26)

V 3^{( 5} ) = ¹

Рассматривая поставленную задачу при условии, что функции G u ( т ) и G y ^{( т} ) определены формулами (5), (6), для нахождения решений интегро-дифференциального уравнения из (26) можно, например, обратиться к методу Эйлера численного решения дифференциальных уравнений. При этом для расчета интегральной части уравнения из системы (26) можно применить, к примеру, одну из квадратурных формул.

Таким образом, задав необходимые параметры и подставив численно выраженные слагаемые в интегро-дифференциальное уравнение из (26), определяют все значения функций сопряженных переменных, после чего можно перейти к (21) и нахождению оптимальной рекламной стратегии фирмы.

Рассмотрим случай, когда функции G u ( т ) и G y ^{( т} ) представлены в виде (7), (8). Покажем, что в данном случае решение задачи можно заметно упростить. Систему дифференциальных уравнений (26) можно переписать в виде следующей системы уравнений:

- b„s            bt

V i ( 5 ) = - a y V i ( 5 ) - 1 - a y b y e y J ( V i ( t ) e y ) dt ,

s

V 2^{( 5} ) = V i^{( 5} ),

V з ( 5 ) = 1-

Для решения системы (27) введем дополнительную функцию

T_b p ^{( 5} ) = J ⁽ V i ⁽ t ) e^yt ) dt ,

s

при этом очевидно, что p(T ) - 0.

Из уравнения (28) выразим производную функции сопряженной переменной:

V 1 ( 5 ) = - p ( 5 ) e b y ⁵ + b y e b y ⁵ p ( 5 ),        ⁽²⁹⁾

где p (5) = dp*5), p( 5) = dipt5!. d5            d52

Преобразовав интегро-дифференциальное уравнение из (24) путем подстановки (28) и (29), получим следующую систему уравнений:

p(5) = -(p(5)e-by5(ay - by) - 1 - aybye-by5p(5))eby5, < p (T) = 0, p (T) = 0.                                       (30)

После решения системы (30), определения первой и второй производных функции p ( 5 ) находятся решения системы уравнений (27) и решение (21), рассчитываются оптимальные затраты на рекламу исходя из (22).

Для определения полученной суммарной прибыли на плановом периоде в соответствии с (1), (10), (25) и рассчитанными оптимальными затратами на рекламу можно также воспользоваться одним из известных численных методов расчета определенных интегралов.

• 1.    Jian Huang, Mingming Ltng, Liping Liang. Recent Developments in Dynamic Advertising Research // European Journal of Operational Research, vol. 220, Issue 3, 01.08.2012, p. 591—609.

• 2.    Берндт Э. Р. Практика эконометрики: классика и современность : учеб. : пер. с англ. М. : ЮНИТИ-ДАНА, 2005.

• 3.    Дыхта В. А., Самсонюк О. Н. Оптимальное импульсивное управление с приложениями. М. : Физмалит, 2000.

• 4.    Дмитрук А. В., Осмоловский Н. П. Необходимые условия слабого минимума в задачах с интегральными уравнениями // Тр. 12 Всерос. совещ. по проблемам управления. М., 2014. С. 709—713.

• 5.    Лутошкин И. В. Моделирование отдачи от частоты рекламных воздействий // Прикладная эконометрика. 2010. № 3(19). С. 101—111.

• 6.    Лутошкин И. В. Оптимизация нелинейных систем с интегро-дифференциальными связями методом параметризации // Изв. ИГУ. Сер. Математика. 2011. Т. 4, № 1. С. 44—56.

• 7.    Лутошкин И. В., Ямалтдинова Н. Р. Инновационные технологии управления на основе динамического моделирования рекламного бюджета // Тр. 5-й Всерос. науч.-практич. конф. с междунар. участием «Региональная инновационная экономика: сущность, элементы, проблемы формирования». Ульяновск, 2014. С. 43—46.

• 8.    Лутошкин И. В., Ямалтдинова Н. Р. Модель оптимизации рекламных расходов с учетом распределенного запаздывания // Сб. тр. 4-й Междунар. науч.-практич. конф. «Математика, статика и информационные технологии в экономике, управлении и образовании». Тверь, 2015. С. 84— 89.