Применение раскрашенных временных сетей Петри для моделирования цементного производства

Введение. В работе рассмотрена методика создания модели на примере сложной распределенной системы — технологического процесса функционирования цементного производства. Процесс выпуска цемента является одним из примеров недетерминированных динамических параллельных производственных систем, проблема моделирования которых связана как с возможной хаотичностью системы, так и с необходимостью учитывать динамику подсистем.

Для описания и анализа таких систем могут применяться сети Петри [1–3] и их разновидности, например, нечеткие [4], временные [5–6], раскрашенные [7].

В [8–10] рассмотрены окрестностные модели обжига клинкера цементного производства. В [11] при моделировании процесса функционирования цементного производства использованы временные сети Петри, достоинствами которых являются динамическое отражение состояний моделируемой системы и возможность анализа свойств полученной модели.

В работе рассмотрены раскрашенные временные сети Петри, являющиеся сетями более высокого уровня и позволяющие, по сравнению с обычными сетями Петри, анализировать дополнительные свойства моделируемых процессов без усложнения структуры сети.

Так, во временных сетях, в отличие от обычных сетей Петри, переходы срабатывают с некоторой задержкой, а маркеры находятся в позициях определенное время, что дает возможность моделирования не только последовательности событий, но и их привязку ко времени.

Раскрашенные сети Петри позволяют одновременно моделировать несколько параллельных потоков различных материалов или событий в процессе функционирования сложных систем. В аналогичных моделях на основе обычных сетей Петри приходится искусственно вводить дополнительные позиции, не являющиеся отображениями элементов процесса, служащие для упорядочения запусков переходов сети и разделения материалов или событий, что усложняет пространственную структуру модели и затрудняет ее интерпретацию.

Раскрашенные временные сети Петри, используемые в работе, объединяют в себе приведенные достоинства как раскрашенных, так и временных сетей.

В работе построен опытный образец модели расчёта объема выпуска продукции цементного производства по месяцам в течение одного года на основе раскрашенных временных сетей Петри.

Разработана программа на языке C++, позволяющая рассчитать производительность цементного производства за заданный период. Реализованная модель с достаточной точностью предсказывает объем выпуска продукции.

Способы задания и правила функционирования сетей Петри . Существует три эквивалентных способа задания сети Петри: графический, аналитический и матричный [3, 11].

Графически сети Петри представляются в виде двудольных графов. Множество вершин состоит из непересе-кающихся подмножеств позиций P = { p_t }, i = 1, _ , n и переходов T = {t j }, j = 1, . , m , а множество дуг разделяется на два подмножества {( p i , t j )} с P х T и {( t j , p i )} с T х P . В изображении графов, представляющих сети Петри, позиции обозначаются кружками, а переходы — планками.

Далее рассмотрим аналитическо-матричный способ задания сетей Петри [11]. Сеть Петри задается следующим набором PN = ( P , T , R ^- , R ⁺ , ц ₀) , где:

• -    P = { p_p p 2 , . , p_n } — конечное непустое множество позиций;

• -    T = { t j, 1 ₂,..., t m } — конечное непустое множество переходов (множества P и T не пересекаются: P П T = 0 );

• -    R - е R m ^{х n} — матрица инцидентности дуг, входящих в переходы;

• -    R ⁺ е R m ^{х n} — матрица инцидентности дуг, выходящих из переходов;

• -    ц ₀ = { ц 1 , Ц ₂, . , Ц _n } — вектор начальной маркировки сети Петри.

Приведем алгоритм функционирования сети Петри:

• 1.    Текущая маркировка сети равна начальной ц = ц ₀ .

• 2.    Переход t j ( j = 1,..., m ) при текущей маркировке ц разрешен, если ц> e j ■ R ^- , где e j = [0,0, . ,1 j , . ,0] е R m — строка, содержащая нули везде, за исключением j -го элемента. Заметим, что разрешенных переходов при текущей маркировке может быть несколько. Если нет разрешенных переходов, сеть достигла тупиковой маркировки, дальнейшее функционирование невозможно, конец алгоритма. Иначе переходим к пункту 3.

• 3.    Случайным образом выбирается один из разрешенных переходов t j ( j = 1,..., m ).

• 4.    Маркеры перемещаются из входных позиций выбранного перехода t j во все его выходные позиции по формуле ц = ц + e j ■ R , где R = R ⁺ - R ^- — матрица инцидентности сети Петри.

Виды сетей Петри. Раскрашенная временная сеть Петри . Во временных сетях Петри [5] PN_pt = ( P , T , R ^- , R ⁺ , Ц ₀, Z , S ) вводятся в рассмотрение временные задержки маркеров в позициях и время срабатывания разрешенных переходов, где:

• -    S = { S j , S 2 , . , S_n } — вектор задержек маркеров в позициях;

• -    Z = { Z 1 , Z 2 , . , Z m } — вектор времени срабатывания разрешенных переходов.

Раскрашенная сеть Петри [7] PN c = ( P, T, С, R - , R ⁺ , ц ₀) отличается от PN наличием цветов, матрицей, а не вектором, начальной маркировки и блочной структурой матриц инцидентности, где:

• -    С = { с1,c2,...,c d } — цвета сети;

• -    Re R ⁽ d ' m ^{) x} n — блочная матрица инцидентности дуг, входящих в переходы;

  R -

  
  

  R 1

  
  
  
  
  
  

  R -

  
  

  , где R k — матрица инцидентности входящих дуг цвета C k , к = 1,

  
  

  ...

  
  

  , d ;

  
  

L Rd\

- R ⁺

e R ^{( d} ' m^{) x} n — блочная матрица инцидентности дуг, выходящих из переходов;

R ⁺

^- Ц о

R +

R 2 +

R

e R

, где R k + — матрица инцидентности выходящих дуг цвета С_к ;

* d _ dxn — матрица начальной маркировки.

Обобщением временной и раскрашенной сети является раскрашенная временная сеть Петри PN cpt = ( P , T , С , R - , R ⁺ ,ц о , Z , S ).

Представление цементного производства посредством раскрашенных временных сетей Петри. Рассмотрим в данном пункте реализацию модели на примере сложного распределенного объекта — технологического процесса функционирования цементного производства ЗАО «Липецкцемент».

На рис. 1 изображен граф раскрашенной временной сети Петри, иллюстрирующий производственный цикл цементного производства.

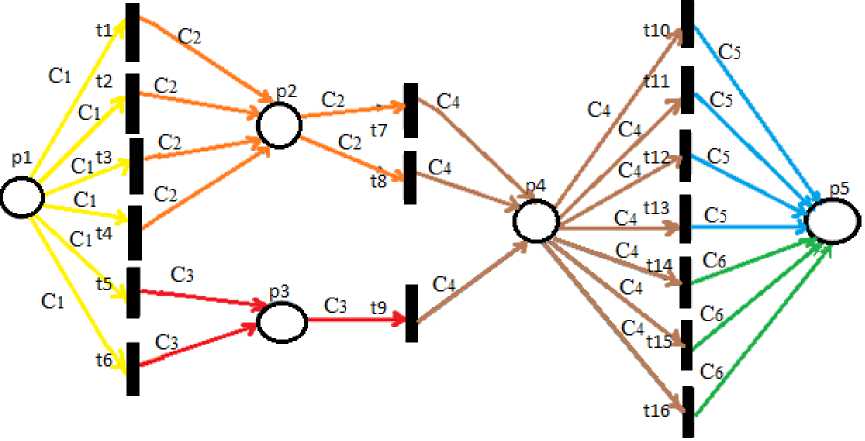
Рис. 1. Граф раскрашенной временной сети Петри цементного производства

Позиции p ₁ – p ₅ на рис. 1 соответствуют следующим складам:

• –    p ₁ — склад сырья;

• –    p ₂ — силос сырьевой муки;

• –    p ₃ — силос сырьевой муки;

• –    p ₄ — склад клинкера;

• –    p ₅ — силос цемента.

Переходы t ₁ – t ₁₆ соответствуют агрегатам:

• -    t 1 — 1 4 — сепараторные мельницы 3,2 X 8,5 м;

• -    t 5 - t 6 — трубные мельницы 4,2 X 10 м;

• -    t 7 - t 8 — вращающиеся печи 4 X 60 м;

• -    t 9 — вращающаяся печь 5 X 75 м;

• -    t ₁₀ - 1 13 — цементные мельницы 3X14 м;

• -    t ₁₄- 1 ₁₆ — цементные мельницы 3,2X15 м.

Граф сети Петри имеет цвета C = { C 1 , C 2 , C 3 , C ₄, C 5 , C 6 } (рис. 1).

Блочные матрицы инцидентности входов и выходов переходов R и

R ⁺ соответственно равны:

R -

R +

R ^-

R

, R ⁺

R

R -

. R 6 +

В частности, для цвета C ₂ матрица R ₂ равна:

R 2 = Г0 0 0 0 0 0 0  0 0000000 01 0  0  0  0  0  0  Г27-  Г228-  0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  0 00000000, 0 0 0 0 0 0 0  0 00000000 _0 00000 0 0 0000000 0_ где r2j — количество сырья, поступающего со склада p2 во вращающуюся печь tj (j = 7, 8). Остальные элементы матрицы R2 равны нулю, так как в графе сети Петри имеется только две входящие оранжевые дуги C2 , соответству- ющие переходам t7 –t8 и позиции p2 (рис. 1).

Матрица R + равна:

0 0 0 0 000000000000

R 2

Г 2²1 ⁺   г£  Г 2²з ⁺   Г 224 ⁺   0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 000000000000

0 0 0 0 000000000000

0 0 0 0 000000000000

где r ₂ ² + — производительность сепараторной мельницы t j ( j = 1,

4). Другие элементы матрицы R 2 являются

нулевыми, так как в графе имеется только четыре выходящие оранжевые дуги C ₂ , соответствующие переходам t ₁ – t ₄ и позиции p ₂ (рис. 1).

Остальные матрицы R k , R k ( k = 1,...,6) формируются аналогично.

Раскрашенная временная сеть Петри цементного производства функционирует по следующему алгоритму:

• 1.    Начальное время функционирования сети т = 0; начальная маркировка ц ₀ описывает количество материала на складах в начальный момент времени; время функционирования производства равно Т часов. Все переходы сети Петри являются незаблокированными.

• 2.    Незаблокированные переходы сети t j , j = 1,..., m' последовательно проверяются на разрешенность. Пере

• 3.    Маркеры перемещаются в разрешенный переход t_j . Результат начала запуска перехода t_j при текущей маркировке ц_т записывается как ц_т = ц_т - e j ® R - . Далее переход блокируется на время S j выполнения операции.

• 4.    Сдвиг времени на τ =τ+ 1 час. Если τ≥Τ , то алгоритм завершен. Маркеры переходят в выходные позиции разрешенных в п.3 незаблокированных в данный момент времени переходов t_j по следующей формуле µ_τ=µ ^' _τ+ e_j ⊗ R ⁺ . Переход к п.2.

ход t j при текущей маркировке ц_т разрешен, если ц_т >  e j ® R , где e j- = [0,0,... ,1 j , ^ ,0] — строка, содержащая нули везде, за исключением j -го элемента; операция ® означает произведение строки e j на каждую из матриц R ^- , образующих блочную матрицу R ^- = Г R f, R ₂ ,..., R d"^ . Если нет разрешенных переходов, переход к п.4.

Переход к п.2.

По данному алгоритму была разработана программа на языке C++, целью которой является моделирование динамики состояний системы и вычисление объема выпуска продукции цементного производства за определенный период.

Рассмотрено функционирование модели на основе реальных данных за 2012 год. Результаты, полученные в процессе моделирования, приведены в табл. 1.

Таблица 1

Относительная ошибка выпуска продукции

Месяц	Относительная ошибка моделирования, %
январь	0,134940
февраль	0,480579
март	0,691856
апрель	0,080636
май	0,257613
июнь	0,099582
июль	0,235929
август	0,036875
сентябрь	0,076327
октябрь	0,407839
ноябрь	0,452516
декабрь	0,071766

Относительная ошибка найденного объема выпуска продукции вычисляется по формуле:

δ P i

~ yi- yi yi

*100%,

где y_i — реальные данные выпуска продукции за i -ый месяц ( i = 1,...,12) ; y i — модельные данные выпуска продукции за i -ый месяц.

Средняя относительная ошибка моделирования составляет 0,25% и является допустимой для применения предложенной модели при прогнозировании объема выпуска продукции цементного производства. Таким образом, проведенные расчеты свидетельствуют об адекватности разработанной модели.

Заключение. В работе реализовано представление раскрашенных временных сетей Петри в матричной форме, сформулирован алгоритм их функционирования.

Раскрашенные временные сети Петри применены в моделировании сложного распределенного объекта — цементного производства. В качестве приложения рассматривается ЗАО «Липецкцемент».

Разработано программное обеспечение на языке C++ для реализации модели функционирования цементного производства. Проведено сравнение результатов моделирования с фактическими данными. Оценена пригодность разработанной модели для прогнозирования производственных процессов на основе данных 2012 года.

Реализованная модель с достаточной точностью предсказывает объем выпуска продукции и может быть эффективно использована для прогноза и анализа динамики производственных процессов.