Применение распределения ципфа для анализа результатов анкетирования

Необходимость изучения данного аспекта обуславливается тем, что в информационномпотоке за день через людей проходит большое количество информации, некоторая из них имеет обратную связь, а на основе полученных результатов (информации) и решаются многие составляющие какой–либо задачи. Для этого нам надо определить подходят ли сведения, являющиеся результатамиопроса, под какое-нибудь распределение.

Ряд распределения – расположение совокупности единиц в определённом порядке по определённым группам. При помощи разложения в ряд появляется возможность исследоватьне объект в целом, а его свойства, раскладывать любую математическую функцию на суммуэлементов, которые в дальнейшей работе проще исследовать.

Закон распределения – это вероятность того, что отдельно взятое событие наступит в соответствии со взятым законом. Выполнение такого закона характеризуется мате-матическиможиданием, дисперсией, функцией распределения и т.д.

Обработка результатов анкетирования – многошаговый процесс, использующий разнообразные методы: от графической обработки и вычисления показателей описательной статистики до корреляционно-регрессионного, факторного, кластерного анализа.

Корреляционный анализ позволяет установить характер и степень выраженности связей между различными показателями. Критерии различий устанавливают достоверность различий между разными группами по определенным показателям. Факторный анализ позволяет объединить группы показателей в единые взаимосвязанные системы и выявить базовые характеристики, их объединяющие. А кластерный — объединить представителей опрашиваемых, сходных по определенным показателям в общие группы.

Важным моментом является определение закона распределения исследуемой случайной величины, которая характеризуетпредметы и явления. Случайной величиной определяют величину, принимающей под влиянием неких

Таблица 1. Фрагмент анкеты

1	Что больше всего помогло Вам сдать успешно ЕГЭ по математике: a) хорошая подготовка в школе; b)    занятия с репетитором; c)    онлайн курсы; d)    самостоятельная подготовка.	Укажите ответы в порядке убывания значимости (в начале самый важный)
2	Как Вы готовились к экзамену (зачету) по математике в вузе: а)    по конспектам; b)    по учебникам; с)    по задачникам; d)    по объяснениям товарищей; e)    специально не учил, а использовал то, что запомнил на занятиях; f)шпаргалки писал.	Укажите ответы в порядке убывания значимости (в начале самый важный)
3	Теоретический материал по математике: а)    понимаю на лекции; b)    разбираюсь в нем на ПЗ; с)    учу наизусть; d)    читаю по учебникам; e)    не учу, предпочитаю только задачи решать.	Укажите ответы в порядке убывания значимости (в начале самый важный)
4	Освоению курса математики в вузе Вам особенно помогает: a)    самостоятельное чтение учебной литературы; b)    ведение конспектов лекций; c)    решение задач на ПЗ; d)    решение КДЗ; e)    решение задач на самоподготовке; f)    обсуждение с товарищами; g)    решение задач нестандартных или повышенной сложности; h)    консультации с преподавателями; m)    решение задач прикладного содержания.	Укажите ответы в порядке убывания значимости (в начале самый важный)
5	Вы считаете, что математика Вам нужна для: a) изучения спец. дисциплин в дальнейшем; b) общего развития; c)    развития алгоритмического мышления и логики; d)    научной работы.	Укажите ответы в порядке убывания значимости (в начале самый важный)
6	Вы считаете математику наукой прежде всего: a) красивой; b)    важной; c)    сложной; d)    полезной.	Укажите ответы в порядке убывания значимости (в начале самый важный)

обстоятельств различные числовые значения. В обычной ситуации случайной величинойможет выступить количество заболевших и пришедших на прием к терапевту, продолжительность жизни человека. В математической науке – это длина, температура, давление. Если эта величина имеет определенные установленные положительное значения (число курсантов в аудитории, частота пульса и др.), то ее определяют дискретной. Если величина приобрела значение внутри конечного или бесконечного интервала (объем мозга, рост взрослого человека), то ее определят, как непрерывная. На данный момент известно множество законов распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, гипергеометрический, нормальный, равномерный, показательный и т.д.

В нашем случае мы рассмотрим соответствие между возможным значением дискретной случайной величины и ее вероятностями, которое трактуется как закон распределения данной величины.

Для определения случайных величин мы проведём анкетирование, участие в котором будут принимать курсанты высшего учебного заведения. Цель исследования – выявление уровня мотивации при изучении математики в высшей школе. В анкетировании приняли участие 73 курсанта первого курса. Многие вопросы предусматривали ответы в виде ранжированных списков (таблица 1).

При обработке результатов анкетирования ранжированные списки после упорядочения представляли собой обратную зависимость. Из известных законов распределения такой характер имеют законы Бредфорда и Ципфа. Однако, эти законы в основном применяются в семантическом анализе [3].

Семантика – с одной стороны, это один из разделов лингвистики, который изучает смысловое значение единиц языка[1], с другой стороны, это семантическое ядро текста с некоторым «облаком» слов, входящих в основной запрос и имеющих с ним общую тематику. Слова из семан-тическогоядра — это те слова, которые пользователь вводит в строку поиска вместе с запросом, чтобы уточнить, что ему нужно.

Семантический анализ – алгоритм понимания текстов, смысл которого – выделение бинарных отношений между изучаемыми текстами и единицами языка. Данный алгоритм является структурой, которая состоит из текстовых фактов [3].

Результаты семантического анализа могут применяться для решения задач в таких областяхкак, например, психиатрия (для диагностирования больных), политология (пред-сказаниерезультатов выборов), торговля (анализ “востребованности” тех или иных товаров на основекомментариев к данному товару), филология (анализ авторских текстов), поисковые системы, системы автоматического перевода и т.д. [3]

Решено было не только проверить применимость этих законов к результатам анкетирования, но и определить, какой из них будет наиболее достоверный: закон распределения Бредфорда (наибольшая информация получается от наименьшего числа информаторов) или закон распределения Ципфа (если всю информацию упорядочить по убыванию частотности их использования, тогда частотность n-го слова в этом списке будет обратно пропорциональной его номеру).

Отсортированная последовательность образует так называемое ранговое распределение, в котором обнаружива- ется отрицательная взаимосвязь между рангом r и частотой fr. Эта взаимосвязь может быть приближенно описана степенной функцией с отрицательным показателем. В самом простом случае это имеет вид: (аппроксимация с одним параметром С). В таком случае говорят, что закон Ципфа удовлетворяет «гиперболическому ранговому распределению». Более общий вид зависимости: (аппроксимация с двумя параметрами С, γ). " r7

Если прологарифмируем функции, то общность рассуждений в плане поведения функции не нарушится, но наглядность улучшится. Получим:

In /J = In C - In г и In /2 = In С - /Un r

Для определения параметров распределения используем метод наименьших квадратов. Например, для двухпараметрической аппроксимации получим следующие формулы( k - общее число рангов):

/^lnr + ^ln/_r ^Inr-^ln/.-А>^1пУ_г-Inr InC =          ----и у = ^--------_k—.

A             A"-^ln2r-^lnr -^hr r=l         rd       rd

Мы воспользовались встроенными возможностями табличного процессора Excel, подбирая степенную линию тренда.

Подсчеты велись по накопительной схеме. То есть сначала подсчитывали, какое число респондентов поставили этот ответ на 1-е место, затем – какое число респондентов указали его среди первых двух ответов, и так далее по возможности (зависело от числа предлагаемых ответов). Результаты заносили в таблицы, по которым строили дополнительные таблицы с упорядоченными по убыванию значениями. (табл.2)

Таблица 2. Расчетные данные по определению особенностей усвоения теоретического материала по математике

	1 m	1 - 2 m			1 m		1 - 2 m
a	17	39		b	40		b	63
b	40	63		a	17		a	39
c	4	26		e	9		c	26
d	3	26		c	4		d	26
e	9	18		d	3		e	18

На основании данных таблиц уже строились графики зависимостей. Затем средствами Excel подбирали линию степенного тренда с указанием уравнения и величины достоверности аппроксимации (рисунок 1).

То есть в теоретическом материале по математике курсанты в основном разбираются на практических занятиях и понимают его на лекциях. Подобранная степенная функция имеет большую величину достоверности аппроксимации (порядка 97%).

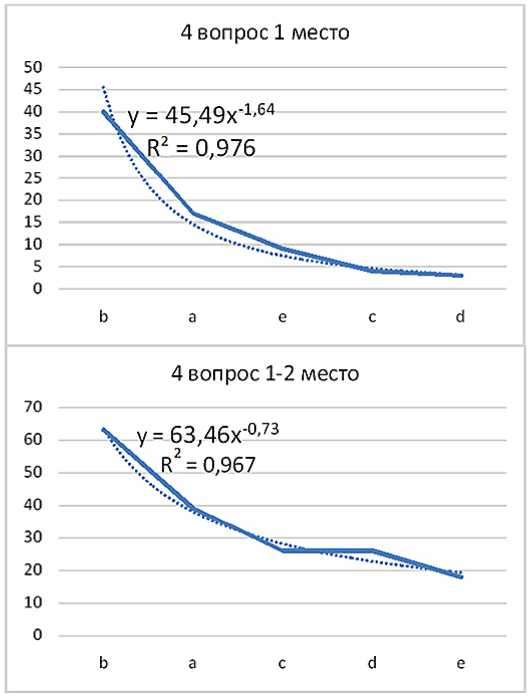
Рисунок 1. Результаты аппроксимации по 4 вопросу (1, 1-2 место)

В плане проводимого исследования большую величину достоверности при аппроксимации этого вида получили вопросы, касающиеся непосредственных действий респондентов:

Вопрос 2. Что помогло сдать ЕГЭ? ( R ² ≈ 0.79)

Вопрос 3. Как готовились к экзамену (зачету) в вузе? ( R ² ≈ 0.79)

Вопрос 4. Как понимается теоретический материал по математике? ( R ² ≈ 0.98)

Вопрос 5. Что особенно помогает освоению курса математики? ( R ² ≈ 0.89)

А вот вопросы, требующие общих умозаключений (о будущем, отношение к науке), с большой натяжкой можно аппроксимировать зависимостью закона Ципфа.

Вопрос 6. Для чего Вам нужна математика? ( R ² ≈ 0.59)

Вопрос 7. Какой наукой Вы считаете математику? ( R ² ≈ 0.68)

Исследование величины достоверности аппроксимации в зависимости от накопления обработанных результатов привело к выводу, что лучшие результаты аппроксимации данного вида наблюдаются при использовании ответов без накопления (когда учитывали число респондентов, которые поставили этот ответ на 1-е место) (рисунок 2).

В статье проанализированы результаты анкетирования с ранжированными списками, удовлетворяющими гиперболическому ранговому распределению, как и в законе

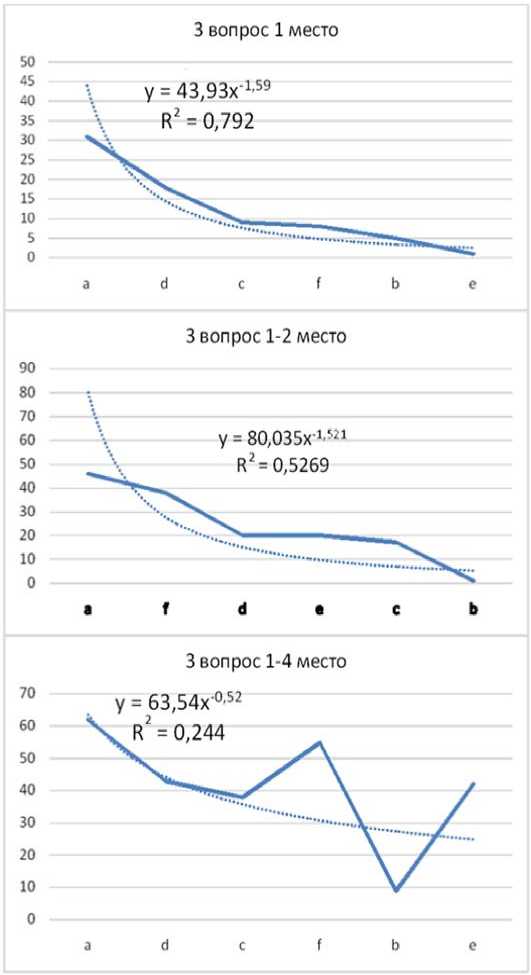
Рисунок 2. Результаты аппроксимации по 3 вопросу (1, 1-2, 1-4 место)

Ципфа. Результаты анкетирования обработаны с помощью возможностей табличного процессора Excel. При увеличении числа рангов величина достоверности аппроксимации увеличивается. При использовании накопленных результатов достоверность ухудшается. При использовании вопросов, затрагивающих практическую жизнь респондентов, достоверность аппроксимации увеличивается. При использовании более абстрактных вопросов достоверность аппроксимации степенной функцией ухудшается. Таким образом, по результатам нашего исследования закон распределения Ципфа применим для обработки результатов анкетирования с ранжированными списками при достаточно большом числе упорядочиваемых ответов (более 5) и содержащем практикоориентированные вопросы.