Применение разностной схемы экспоненциальной подгонки для численного моделирования нестационарных процессов, протекающих в канале линейного МГД-ускорителя

Планируемые в недалеком будущем пилотируемые полеты к планетам Солнечной системы потребуют разработки ракетного двигателя с высокой тягой и удельным импульсом. Это позволит существенно сократить время пребывания человека в условиях жесткой космической радиации, сократить расход рабочего тела и, соответственно, уменьшить необходимый запас топлива на борту корабля, увеличив тем самым массу полезного груза. Удовлетворить эти требования могли бы электрические ракетные двигатели (ЭРД) – устройства, которые используют интенсивный импульс электрического тока (порядка 104…106 А) для создания высокоскоростной (порядка 103…105 м/с) плазменной струи. Существующие в настоящее время образцы подобного рода устройств нашли широкое применение в космической технике, а также во многих научных экспериментах как источники плазмы. Но, к сожалению, они обладают очень низким уровнем тяги (не более 1 Н), что делает нецелесообразным их применение в качестве маршевых двигателей для космических кораблей.

Низкая сила тяги современных ЭРД связана с самим принципом их работы. Поскольку большинство современных ЭРД работают только с однородным стационарным плазменным потоком, то для предотвращения возникновения различного рода неустойчивостей, стремящихся эту однородность разрушить, данные устройства вынуждены работать при очень низких давлениях, что и обусловливает низкий уровень тяги. Эту проблему может решить создание индукционного ЭРД фарадеевского типа с неоднородной токовой структурой. Существование таких нестационарных, стабильных плазменных структур – так называемых Т-слоев, которые появляются в плазменном потоке, движущемся в поперечном магнитном поле, – было обнаружено в результате численного моделирования в 60-х гг. прошлого века. Т-слои являются результатом развития перегревной неустойчивости, которая в условиях МГД-ускорителя неизбежно возникает, как только плазма из-за охлаждения холодным газом переходит в состояние слабой ионизации. Т-слои – это плазменные поршни, ориентированные вдоль вектора электрического поля и движущиеся вместе с газовым потоком, и поэтому их можно использовать для ускорения неоднородного газоплазменного потока в фарадеевском МГД-канале.

Принципиальная возможность использования Т-слоя для данных целей была показана в работах [1–3]. Одномерное численное моделирование работы индукционного ЭРД с неоднородной токовой структурой показало возможность достижения средней скорости на выходе канала порядка 40…50 км/с при величине расхода рабочего тела 10…50 г/с, что обеспечивает значения тяги в диапазоне 400…2 000 Н.

Однако результаты одномерного моделирования не дают ответа на вопрос, является ли токовый слой устойчивым по отношению к многочисленным возмущениям, которые с неизбежностью будут возникать в канале МГД-ускорителя. Так, в частности, в работах [4; 5] был описан эффект так называемого накренения ( canting ) токового слоя, который заключается в отклонении плазменного сгустка от направления, перпендикулярного электродам в канале линейного МГД-ускорителя. Искривленный токовый слой создает поперечную электродам компоненту силы тяги ЭРД, из-за чего появляется дополнительный вращательный момент, который ухудшает управление космическим кораблем. Кроме того, дополнительная поперечная сила тратит энергию на разгон газа, не преобразуя ее в полезную тягу. Таким образом, в данном случае двумерный эффект приводит к существенному ухудшению характеристик МГД-ускорителя. В связи с этим была поставлена задача изучения нестационарных двумерных процессов в канале линейного ускорителя, чтобы построить и отработать на имеющихся экспериментальных данных математическую модель, которую затем можно будет использовать для более детального изучения процессов в разрабатываемом индукционном ускорителе фарадеевского типа.

Физическая модель. Для проведения численного моделирования процесса ускорения плазменного сгустка использовались данные эксперимента, описанного в [4; 5]. Линейный МГД-ускоритель, или рельсотрон (рис. 1), представляет собой два медных электрода, разделенных диэлектрической вставкой и подключенных к электрической цепи с батареей конденсаторов емкостью 10 мкФ и катушкой индуктивности 100 нГн. Боковые стенки ускорителя выполнены из прозрачного материала – пирекса – для проведения скоро стной фотосъемки. Длина МГД-канала 60 см, ширина 10 см, расстояние между электродами 5 см.

В начальный момент МГД-канал заполнен холодным непроводящим аргоном при давлении 100 мторр. При замыкании электрической цепи в МГД-канале происходит пробой холодного газа, формируется дуговой разряд, который затем развивается в токовый слой. Возникающее при этом магнитное поле, параллельное плоскости электродов, ускоряет плазменный сгусток. Под действием теплового и силового факторов происходит формирование плазменного поршня (Т-слоя), который ускоряет участок газового потока, оказавшийся перед ним. Впереди Т-слоя следует сжатый им массовый сгусток, плотность которого резко падает при переходе к волне разрежения, возникающей за Т-слоем. Низкое давление плазмы в хвосте токового слоя приводит к тому, что параметр Холла в волне разряжения становится достаточно большим. В результате возникает холловская компонента силы тока, а вместе с ней -и перпендикулярная потоку компонента силы Лоренца, которая способствует тому, что токовый слой отклоняется от ортогонального к электродам направления (рис. 2).

Рис. 1. Фотографии экспериментальной установки

Следующей фазой развития Т-слоя является фаза «снежного плуга», которая начинается, когда искривленная токовая ветвь соединяется с катодом. Непроницаемый для холодного газа Т-слой, подобно плугу, сгребает газ впереди себя. Основной плазменный канал, оторвавшийся от анода, движется к катоду и на стадии «снежного плуга» превращается в след, который тянется за токовым слоем. Более детально процессы, происходящие с токовым слоем в канале ускорителя, описаны в [4]. Нас же больше будет интересовать непосредственное влияние на плазменный сгусток эффекта Холла. Для изучения этого влияния обратимся к численному моделированию.

Математическая модель. Для численного моделирования описанного выше процесса решалась полная система двумерных уравнений магнитной газодинамики, которая, помимо законов сохранения массы, импульса и энергии, включала уравнение индукции магнитного поля с учетом эффекта Холла.

Уравнение неразрывности было следующим:

^^( Р ^{- и} ) + ^( р- ^v ) = ^{5 (} T ) ,        ⁽¹⁾

д t дx        ду где 5 (T) - источниковое слагаемое, отвечающее за увеличение массы газа в МГД-канале, связанное с интенсивной эрозией электродов. Значение этого источника находилось из эмпирического соотношения, а величины входящих в соотношение коэффициентов подобраны в результате методических расчетов:

5 (T ) = 0,5 - e (-1,5/Т).(2)

Закон сохранения импульса с учетом силы Лоренца представлен в виде

• —    (р-и) + —(р-и2 + PA + — (р-v■ и) = j - B, (3) д t         дx              ду

д        дд

• —    (р-v) + —(р-v + P) 1_ (Р-v-u) = -j -B, (4) д t         ду '         ’ дx

а закон сохранения энергии с учетом джоулевой диссипации и радиационных потерь - в виде

• —    + — (u (e + P)) +—(v (e + P)) = J - E - q , (5) д t дx             дуу

где e - полная удельная энергия плазмы; P - давление газа; и и v - компоненты вектора скорости потока; р -плотность газа.

Рис. 2. Фотографии токового слоя через каждые 3 мкс [4]

В качестве уравнения состояния аргона использовалось уравнение идеального газа.

Радиационные потери энергии из объема плазмы, расчет которых даже в грубом приближении является сложной проблемой, в данной модели учитывались как величина, пропорциональная T4. Коэффициент пропорциональности подбирался с таким расчетом, чтобы радиационные потери стабилизировали температуру плазмы в Т-слое на уровне 2 -104 К [3]. Такой подход отражает экспериментальные данные о свойствах плазмы в условиях, близких к поставленной нами задаче. Таким образом, радиационные потери в единице объема плазмы брались в виде qr = qо -т4, q0 = 10-                  (6)

Для инициирования токового слоя в начале канала создавалось локальное изобарическое возмущение температуры до максимального значения T max = 10⁴ К.

В качестве граничных условий для газодинамических параметров на твердых стенках ставились условия скольжения и непротекания, на выходе из МГД-канала – условие сноса, т. е. равенства нулю производной по нормали к границе для всех величин.

Распределение электромагнитных величин находилось из уравнений Максвелла, дополненных дифференциальным законом Ома с учетом эффекта Холла: rr

J =’ ( E r + V * B ) - JBB в •

J = ~1— Vx B , Vx E = - — , V- B = 0. (7) Ц ^- Цо                      d t

Объединив эти уравнения, получим уравнение индукции магнитного поля:

---1--V B - B [ V - J^-B,      (8) ц - ц0 - G        (    B -g J I где B – индукция магнитного поля; Jr – плотность электрического тока; в - параметр Холла; g - электропровод -ность плазмы; V – скорость газового потока; E – на- пряженность электрического поля.

Для определения граничных условий в магнитном поле на левой границе расчетной области решалось электро- техническое уравнение цепи c конденсатором и контуром возбуждения, который индуктивно связан с плазмой:

LdI^l + R -1(t)-U(t) = -dф(t) dtdt

/ - e = - d Ф ( t ) dU^IM.

Z dt ' ), dtC ’

¹ ( t ) =

B ( 0, t ) h -Ц 0

, U ( 0 ) = 9 кВ , I ( 0 ) = 0 А,

C = 10 мкФ, L = 100 нГн,(9)

где R – сопротивление цепи; U – напряжение на конденсаторе; Ф - магнитный поток; I - ток в цепи; L - индуктивность плазмы; С – емкость конденсатора; l_z – ширина электродов; h – шаг разностной сетки. На остальных границах задавались условия Неймана:

d B             д B

— = 0 при x = l x , — = 0 при у = 0 и у = l x . (10) д x               д у

В качестве модели плазмы была использована равновесная модель. Электропроводность газа рассчитывалась по эмпирической формуле, качественно верно отражаю- щей поведение реальной плазмы:

G L G _$    „ . 1,53 - 10 ^{- 2} T ^3/2 „ _     п_е ■ e ²

^{G                , G} S         1 / . \      ^{, G} L           tr _т , ⁽¹¹⁾

GL +GS             1П (Л)            me -Gea - Vea где gL - лоренцевская проводимость, обусловленная электрон-атомными столкновениями, которые преобла- дают в плазме при низких температурах; gs - спитце-ровская проводимость, обусловленная кулоновскими электрон-ионными столкновениями, которые преобладают при более высоких температурах.

Концентрация электронов для равновесной плазмы аргона находилась из уравнения Саха:

_      P - K n = -K +1 K<2 +----S e S Л1 S k T ’              V-^*)

K s =

( 2 n m_ekT ) ^3/ 2

^e ₃       exp

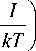
где I – потенциал ионизации атомов аргона; h – постоянная Планка; k – постоянная Больцмана; me – масса элек- трона.

Параметр Холла вычислялся следующим образом:

в =

eB me (V ea +V ei ) ’

v _ei = 8,83 - 10 ^{- 6}

■ n ■ T-3/2 v = и ■ V -с1г ne T , ea       a    ea     ea ’ где vei - частота столкновений электронов с ионами; vea - частота столкновений электронов с атомами.

Численная методика. Расчетная область представляет собой прямоугольник, ограниченный сверху и снизу электродными стенками канала, справа – диэлектрической стенкой, а слева – выходной границей. Простота геометрии задачи позволяет получать численное решение на однородной прямоугольной сетке. Представленные далее результаты расчетов получены на разностной сетке 300 x 60 узлов (размеры расчетной ячейки 2 x 0,8 мм).

Детально численная методика описана в [6], здесь же отметим лишь основные ее моменты.

Пожалуй, наибольшую сложность представляло решение уравнения магнитной индукции (8), характеризующегося сильной нелинейностью, вызванной наличием членов, связанных с эффектом Холла. Как известно, МГД-задачи с эффектом Холла являются неустойчивыми, и поэтому такие задачи обычно решаются через потенциал электрического поля в приближении постоянства магнитной индукции или же с использованием вектора-потенциала магнитного поля. Численная методики [6] позволяет решать уравнение магнитной индукции в той форме, в которой оно записано в уравнении (8). Стоит также отметить, что дифференциальное уравнение (8) по своей природе является задачей с сильно переменными коэффициентами и большими градиентами, что также наложило свои ограничения на выбор метода решения. Преодолеть все описанные выше трудности удалось благодаря использованию абсолютно устойчивой схемы с экспоненциальной подгонкой [7].

Взаимодействие подсистемы Эйлера с уравнениями Максвелла осуществлялось при помощи метода расщеп- ления по физически процессам [8], суть которого состоит в следующем.

На первом этапе учитывались конвективные потоки и

газодинамическая сила, что достигалось решением подсистемы Эйлера явной TVD-схемой Хартена:

r _* r _{n r n r n}

U—U— + ^( G (U ) ) +^ ( H (U ) ) = 0,   (13)

т     dx          ду где U — вектор газодинамических величин; т - шаг по времени, определяемый из условия Куранта; n – номер r*

временного слоя; U – промежуточное распределение.

На втором этапе в результате решения уравнения магнитной индукции находились распределения электричес-

кого и магнитного полей:

В * -

т

B n   д Г . д В        ) *

= I Г - В ■ и I + дx V   дx       J

что образуется ступенчатая структура с резким падением магнитной индукции на Т-слое. Это явление объясняется тем, что Т-слой не полностью экранирует магнитное поле, которое сохраняет достаточное значение. Токовый слой, подобно поршню, увлекает за собой холодный газ, поэтому давление в волне разрежения за Т-слоем сильно падает по мере продвижения плазмы по каналу. Как и ожидалось, низкое давление плазмы в хвосте токового слоя приводит к тому, что параметр Холла в волне разряжения достигает значительной величины. Однако из-за высокой температуры плазмы в МГД-канале происходит непрерывная эрозия электродов, которая обеспечивает приток массы газа в волну разрежения, в связи с чем давление (а вместе с ним и параметр Холла) в хвосте Т-слоя постепенно стабилизируется.

^д Г * ^д В        .)     - к

+--1 Г-- В ■ V I + F .

д У V    д у       )

На третьем этапе учитывались МГД-эффекты (сила Лоренца, джоулева диссипация) и объемные радиацион-

ные потери энергии:

* и — и р------- т

* V — V р------- т

* 8   —8

Р ------- т

=(Л1

О *

— q 0 ( т * /,

где * - номер внутренней итерации; 8 - внутренняя энер-

гия газа.

Для увеличения устойчивости метода производилась корректировка U k ^{+ 1} при помощи метода нижней релаксации:

U * ^{+ 1} =a ( U ^- ) * ^{+ 1} + (1 — a ) U 7 * , (16) где a - параметр нижней релаксации, равный 0,2. После достижения сходимости этого итерационного процесса полученное решение U * ^{+ 1} принималось за решение на новом временном слое.

Результаты моделирования. Все представленные в данной статье результаты приведены в безразмерных единицах, для перевода этих величин в СИ нужно умножить их на соответствующий размерный множитель: T = 10⁴ К, V = 10 3 м/с, P = 10 5 Па, J = 10 5 А/м², E = 10 3 В/м, В = 1 Тл, m = 10 ^{— 1} кг, t = 10 ^{— 3} с.

Для отражения динамики нестационарного процесса приведем одномерное распределение всех параметров по длине канала для четырех последовательных моментов времени (рис. 3). Характер расчетных кривых говорит о том, что начальный плазменный сгусток формируется в токовый слой, температура которого стабилизируется на уровне 2 ■ 10⁴К. Толщина Т-слоя ® 2^3 см, что должно обеспечивать гидродинамическую устойчивость поршневой структуры по отношению к неустойчивости Релея–Тейлора. Сопоставление взаимного расположения скачков плотности и пиков температуры приводит к выводу, что максимум плотности опережает максимум температуры на толщину Т-слоя. Таков непосредственный результат воздействия плазменного поршня на газ. Ана-

лиз распределения магнитного поля в канале показывает,

j

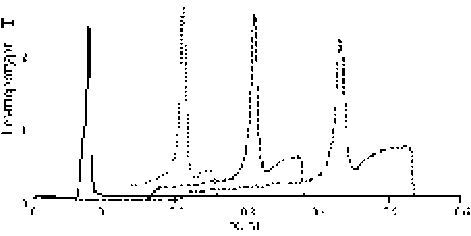
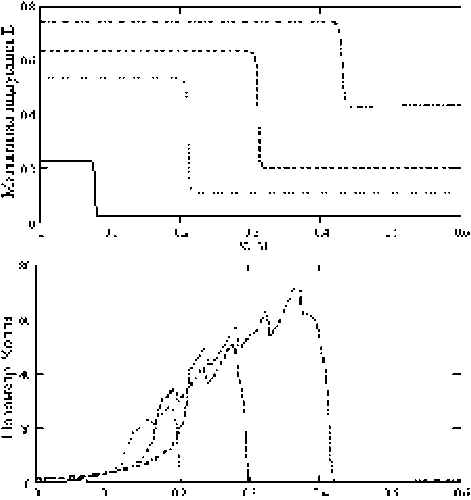
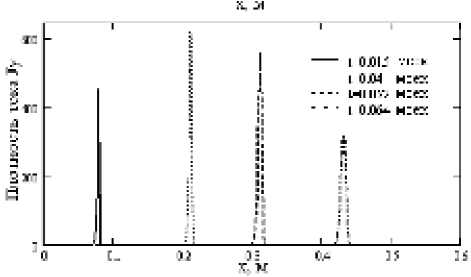
Рис. 3. Мгновенное распределение величин вдоль центральной линии МГД-канала

В используемой авторами численной методике приток массы от горящих электродов моделировался введением источника в уравнение неразрывности. Определение точного количества образующегося газа является весьма сложной задачей, но качественно можно считать, что интенсивность эрозии зависит от температуры по закону Аррениуса. Введение источника в уравнение неразрывности не только привело к уменьшению параметра Холла в волне разрежения до величин, соответствующих экспериментальным, но и в целом стабилизировало расчет.

Для большей наглядности приведем двумерное распределение плотности тока в расчетной области в виде изолинии (рис. 4). Поскольку параметр Холла в МГД-ка-нале намного превышает единицу, то возникает достаточно большая холловская компонента силы тока, а вместе с ней и перпендикулярная потоку компонента силы Лоренца. Эта компонента приводит к тому, что токовый слой, оставаясь непроницаемым для холодного газа, отклоняется от ортогонального к электродам направления, т. е. имеет место ярко выраженное явление накренения плазменного сгустка.

t = 0,015 мс

t = 0,04 мс линейного ускорителя, что подтвердило существование наблюдаемого в экспериментах эффекта отклонения Т-слоя от направления, перпендикулярного электродам.

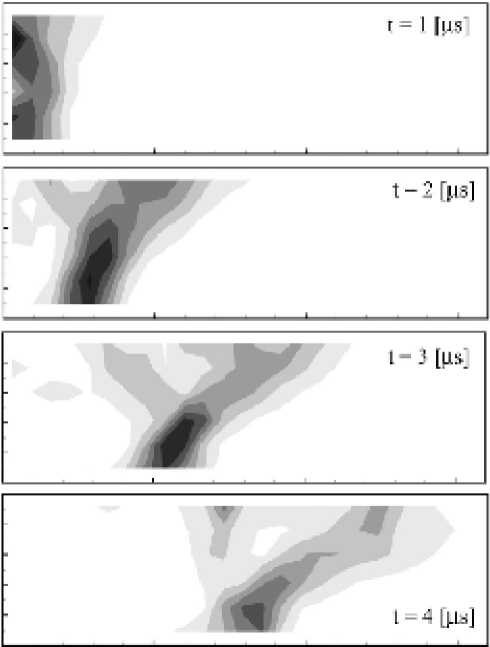
Рис. 5. Экспериментальные изолинии плотности тока в диапазоне от 0 до 400

t = 0,052 мс

t = 0,064 мс

Рис. 4. Изолинии плотности тока в диапазоне от 0 до 640 в различные моменты времени

Полученная система уравнений магнитной газодинамики в рассмотренной постановке хотя и не позволяет полностью описать начальную фазы развития токового слоя, тем не менее дает возможность качественно предсказать его поведение на более поздних этапах. Дальнейшее решение этой проблемы, по-видимому, потребует включения в обобщенный закон Ома слагаемого, связанного с градиентом давления, а также учета вязких сил и турбулентности.

В целом можно отметить, что наличие пространственных эффектов, существенно сказывающихся на работе МГД-устройства, в целом не отвергает идею создания эффективного МГД-ускорителя с неоднородным газоплазменным потоком.

Сопоставление расчетных данных с экспериментальными [2] (рис. 5) показывает, что численные результаты качественно верно описывают поведение Т-слоя в эксперименте.

Таким образом, разработан высокоэффективный численный алгоритм, позволяющий рассчитывать широкий класс двумерных нестационарных сильно неоднородных МГД-течений идеального газа, с большими значениями параметра Холла.

В результате применения разработанного алгоритма решена задача двумерного численного моделирования МГД-процесса эволюции плазменного сгустка в канале