Применение разработанной компьютерной модели для исследования технических характеристик низковольтных коммутационных аппаратов на примере автоматических выключателей

DOI:

Верстунин А. Ю. и др. Применение разработанной компьютерной модели для исследования технических характеристик низковольтных коммутационных аппаратов на примере автоматических выключателей. Вестник МГТУ. 2025. Т. 28, № 4/1. С. 451–464. DOI:

Verstunin, A. Yu. et al. 2025. Application of the developed computer model to study the technical characteristics of low-voltage switching devices using the example of circuit breakers. Vestnik of MSTU, 28(4/1), pp. 451–464. (In Russ.) DOI:

Электроснабжение как промышленных, так и непромышленных потребителей невозможно представить без современного электротехнического оборудования. В настоящее время ужесточаются требования к качеству и эффективности работы низковольтных коммутационных аппаратов (НКА). НКА должны обладать высоким уровнем надежности и безотказно функционировать на протяжении всего срока эксплуатации ( Воронин и др., 2020; Feng, 2024; Hasan et al., 2020 ).

Низковольтные сети систем электроснабжения включают в себя множество контактов и контактных соединений ( Садыков, 2017 ).

Для определения величины потерь электроэнергии в низковольтных цеховых сетях промышленных предприятий необходимы данные о величине сопротивлений и нагреве контактных соединений НКА ( Львов и др., 2024; Atanasov et al., 2022 ). Основными факторами, определяющими данные параметры, являются: номинальный ток аппарата; его коэффициент загрузки; геометрическая форма и материал контактов; сечение токопроводящих частей аппарата и площадь контактного перехода; режим работы и среда эксплуатации ( Верстунин, 2023; Andrei et al., 2023; Grigoras et al., 2018 ).

Как правило, НКА работают в режимах, отличающихся от номинальных. Коэффициент загрузки аппарата может многократно меняться в зависимости от условий и режимов работы. Отметим, что контактная система подвержена также электрическому и механическому износу ( Ковалев и др., 2017; Vorkunov et al., 2025; Wei et al., 2021 ). На данные параметры влияют частота цикла коммутаций, ослабления контактного нажатия, внешние и внутренние вибрации, увеличение шероховатостей поверхности контактной системы.

Низковольтные цеховые сети обычно имеют большую протяженность и сочетают в себе радиальные, магистральные и смешанные участки. Такие сети имеют множество последовательных и параллельных узлов с НКА, поэтому исследование эффективности функционирования аппаратов является актуальной задачей.

Цель статьи – моделирование основных технических параметров контактной системы автоматических выключателей (АВ).

Предлагаемая компьютерная модель позволяет анализировать конструктивные параметры АВ при проектировании или модернизации уже разработанной конструкции аппарата. Разработанная модель дает возможность выявлять ошибки при проектировании конструкции НКА. При этом сокращается число доработок конструкции на любом этапе проектирования, и выбираются оптимальные параметры контактной системы.

Материалы и методы

Моделирование нагрева контактной системы автоматических выключателей

Моделирование процесса нагрева контактов и контактных соединений применяется для определения основных технических параметров. При моделировании возможно определить точки перегрева контактной системы до процесса разработки натурной модели аппарата, сократив при этом количество итераций. Компьютерная модель может быть использована для проведения исследований при разработке новой модели конструкции АВ. Результаты исследований с помощью разработанной модели позволяют определить оптимальные размеры и параметры контактной системы и аппарата в целом.

Разработанная модель позволяет определить следующие технические параметры:

• –    температуру нагрева элементов контактной системы, °C;

• –    потери активной мощности в контактном переходе и на полюс аппарата, Вт;

• –    контактное сопротивление, мОм;

• –    оптимальные геометрические параметры контактной системы;

• –    допустимые значения контактного нажатия и шероховатостей материалов контактов.

Начальным этапом моделирования является разработка геометрической структуры контактной системы в программе Solid Edge, представленной на рис. 1. В разработанной модели представлен наиболее распространенный тип геометрии контактов АВ с рычажным подвижным контактом.

На рис. 1: 1 – рычаг управления; 2 – корпус; 3 – электромагнитный расцепитель; 4 – ввод для клеммы подключения; 5 – неподвижный контакт; 6 – напайка; 7 – подвижный контакт; 8 – гибкая связь; 9 – биметаллическая пластина.

Значения физических параметров в компьютерной модели заданы в программе COMSOL Multiphysics. Кроме основных технических данных задаются параметры, от которых зависит точность результата моделирования: шероховатость поверхности, неровности среднего наклона; шероховатость поверхности, выступы средней высоты; контактное нажатие, кПа; микротвердость, Па; коэффициент теплопередачи, Вт/(м2∙К).

В компьютерной модели были смоделированы контакты АВ с I _ном = 16 А и I _ном = 32 А. Параметры аппаратов должны соответствовать требованиям ГОСТ IEC 60947-2-2021¹ и ГОСТ 60898-1-2020².

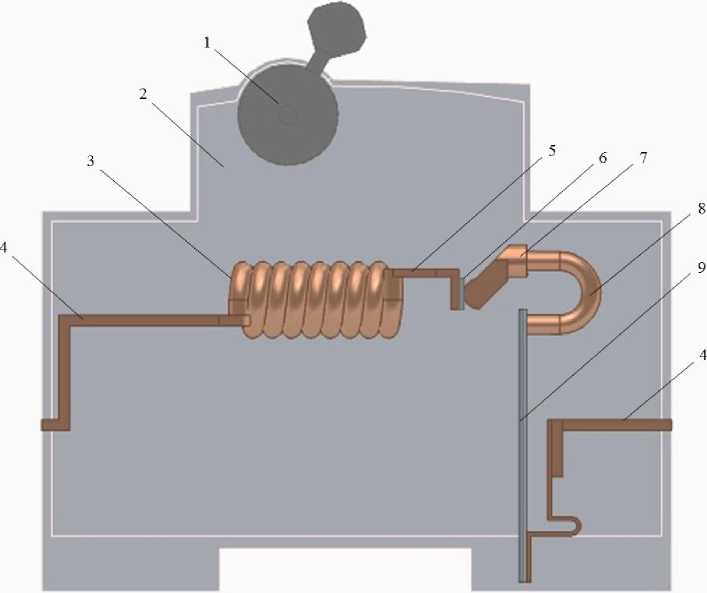
Рис. 1. Модель контактной системы АВ

Fig. 1. Model of the contact system of the CB

Допустимое превышение температуры нагрева контактов регламентирует ГОСТ 403-73³, согласно которого допустимое значение температуры нагрева контактов внутри аппаратов составляет t доп = 105 °C при t ос = 40 °C. На рис. 2 представлено распределение температуры по контактной системе и на корпус АВ с I _ном = 16 А при номинальной загрузке. На рис. 3 – для АВ с I _ном = 32 А.

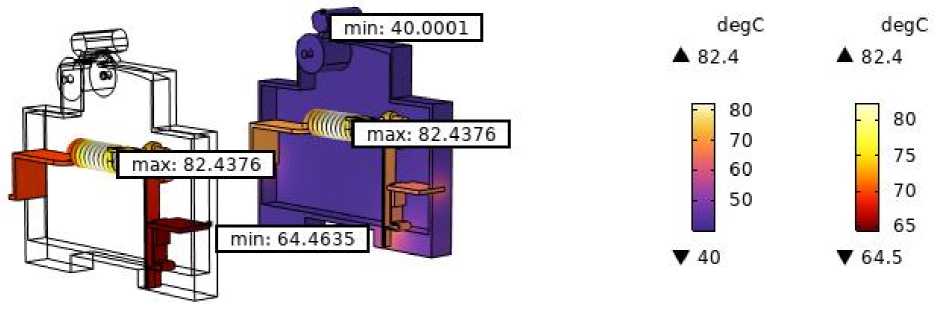
Рис. 2. Распределение температуры по контактной системе и на корпус для АВ c I _ном = 16 А Fig. 2. Temperature distribution across the contact system and on the housing for CB with I _nom = 16 A

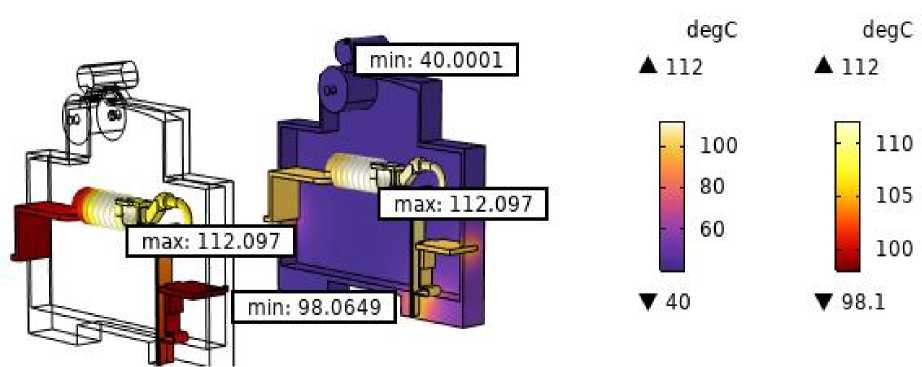
Рис. 3. Распределение температуры по контактной системе и на корпус для АВ c I _ном = 32 А

Fig. 3. Temperature distribution across the contact system and on the housing for CB with I nom = 32 A

Результаты моделирования нагрева контактной системы АВ приведены в табл. 1.

Таблица 1. Результаты моделирования нагрева контактной системы Table 1. Simulation results of heating of the contact system

Тип аппарата	t , °C	К з
		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2
АВ 16А	min	40,2	40,8	41,9	43,5	45,6	48,1	51,2	54,9	59,3	64,5	70,4	77,4
	max	40,4	41,5	43,4	46,1	49,6	54,0	59,4	65,8	73,5	82,4	92,8	105,1
АВ 32А	min	40,5	41,9	44,3	47,8	52,3	58,1	65,3	74,2	84,9	98,1	113,9	133,5
	max	40,6	42,3	45,3	49,5	55,2	62,4	71,4	82,4	95,8	112,1	131,9	156,4

Допустимое значение превышения температуры нагрева контактов использовано для контактов без защитных покрытий контактной поверхности, в качестве материала контактной группы используется медь.

Рис. 2 показывает, что при К з = 1 для АВ с I ном = 16 А, максимальная абсолютная температура нагрева контактов составляет 82,4 °C. Требование ГОСТ 403-73⁴ в этом случае выполняется, перегрева по контактной системе не наблюдается. На рис. 3 для АВ с I _ном = 32 А максимальная абсолютная температура при К_з = 1 составила 112,1 °C. Превышение температуры над допустимым значением составляет t пр = 112,1 °C – 105 °C = 7,1 °C.

В АВ напайка на контакт выполняется из композитных материалов на основе серебра, что значительно увеличивает допустимое значение температуры нагрева контактной системы. Для аппаратов на номинальные токи до 16 А в качестве материала контактной группы допустимо применять медь с использованием защитного покрытия, а для аппаратов на номинальные токи больше 16 А необходим композит как материал контактной группы.

Результаты и обсуждение

Для определения значения температуры нагрева контактной системы АВ расчетным методом используем выражение t расч

( I ном - К з )² - Р + t ос - F ■ k т - S F ■ k _г ■ S - ( I ном ■ К з )² ■ Р ■ а

°C,

где I _ном - номинальный ток АВ, А; К з - коэффициент загрузки; р - удельное электрическое сопротивление, Ом^м; t _ос - температура окружающей среды, ° С; F - охлаждающая поверхность проводника, м²; к т -коэффициент теплоотдачи, Вт/(м² - К); S - площадь поперечного сечения контактов, м²; а - температурный коэффициент увеличения сопротивления.

Для АВ с Iном = 16 А при Кз = 1 расчетное значение температуры составит t расч

16 2 - 1,7 - 10— 8 + 40 - 2(3,0 + 1,25) - 10^-3 - 16 - 3,0 - 1,25 - 10^-6   _ _{50 4 oc}

2(3,0 + 1,25) - 10 ^{- 3} - 16 - 3,0 - 1,25 - 10 ^{- 6} - 16² - 1,7 - 10 — 8 - 0,0043 ~   ’      ^.

Для АВ с Iном = 32 А при Кз = 1 расчетное значение температуры составит t расч

32 2 - 1,7 - 10^-8 + 40 - 2(3,0 + 1,25) - 10^-3 - 16 - 3,0 - 1,25 - 10^-6   _ _{86 9} o_C

2(3,0 + 1,25) - 10 ^{- 3} - 16 - 3,0 - 1,25 - 10 ^{- 6} - 32² - 1,7 - 10 ^{- 8} - 0,0043 ~   ’     ^.

На рис. 4 и 5 представлено сравнение распределения температуры нагрева в контактной системе расчетным методом и с помощью компьютерной модели.

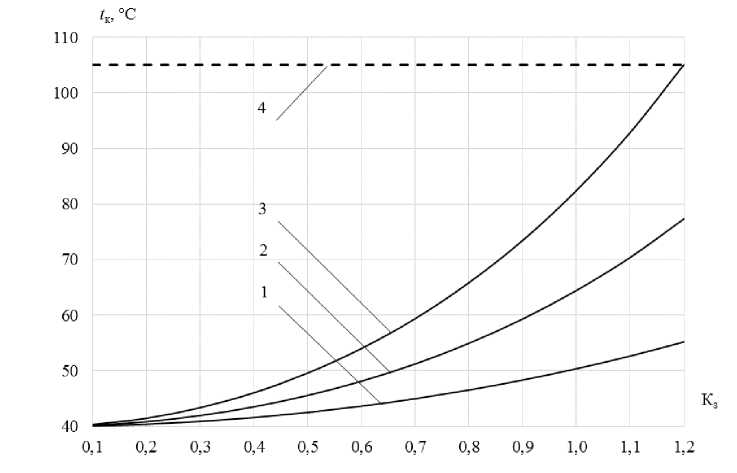
Рис. 4. Графические зависимости температуры нагрева контактной системы АВ c I ном = 16 А от коэффициента загрузки аппарата

Fig. 4. Graphic dependences of the heating temperature of the contact system CB with I nom = 16 A on the device load factor

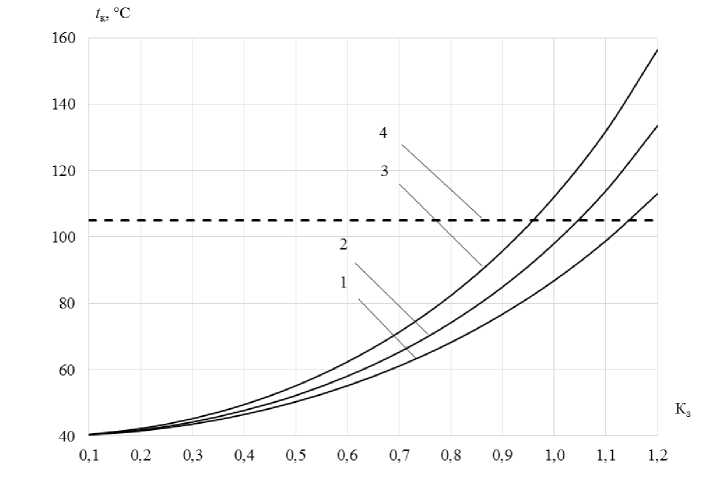
Рис. 5. Графические зависимости температуры нагрева контактной системы АВ c I _ном = 32 А от коэффициента загрузки аппарата

Fig. 5. Graphic dependences of the heating temperature of the contact system CB with I _nom = 32 A on the device load factor

На рис. 4 и 5: кривая 1 – график расчетных значений температуры нагрева контактной системы АВ t _расч, кривая 2 – график значений минимальной температуры нагрева контактной системы АВ по компьютерной модели t мод.мин , кривая 3 – график значений максимальной температуры нагрева контактной системы АВ по компьютерной модели t _{мод.макс}, прямая 4 – график значения допустимой температуры нагрева контактной системы АВ в соответствии с ГОСТ 403-73⁵, t _доп = 105 °C.

Рис. 4 показывает, что при загрузке АВ с I ном = 16 А от 0,1 до 1,2 нагрев контактной системы не превышает допустимой температуры нагрева 105 °C как при определении расчетным способом, так и при определении с помощью компьютерной модели. Для АВ с I _ном = 32 А при определении расчетным способом коэффициент загрузки не должен превышать К з = 1,15, при определении с помощью компьютерной модели не рекомендуется загружать аппарат выше значения К з = 0,95.

Согласно ГОСТ 60898-1-20206 экспериментальное определение температуры нагрева контактов модульных АВ возможно только после 28-суточных испытаний путем замера температуры нагрева на выводах аппарата. Конструктивное исполнение большинства АВ не допускает прямого измерения температуры нагрева контактного соединения внутри аппарата без смещения деталей аппарата, так как это может повлиять на достоверность результатов измерений. Полученные данные с помощью компьютерной модели совпадают с данными после 28-суточных испытаний. В связи с этим считаем, что данные соответствуют экспериментальным значениям нагрева контактных соединений АВ.

Для оценки точности полученных данных температуры нагрева контактной системы АВ определим погрешность вычисления. При этом результаты вычислений температуры нагрева контактной системы АВ, полученные с помощью компьютерной модели, принимаем за достоверные. Результаты расчетов представлены в табл. 2.

Таблица 2. Результаты вычисления погрешностей при определении температуры нагрева контактов Table 2. The results of calculating errors in determining the heating temperature of the contacts

Тип аппарата	δ, %	К з
		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2
АВ 16 А	min	0,3	1,1	2,5	4,4	6,7	9,3	12,2	15,3	18,5	21,8	25,2	28,6
	max	0,6	2,6	5,7	9,7	14,3	19,2	24,2	29,3	34,2	38,9	43,3	47,5
АВ 32 А	min	0,1	0,6	1,4	2,6	3,6	5,0	6,4	8,0	9,6	11,4	13,2	15,3
	max	0,4	1,7	3,6	6,0	8,7	11,6	14,3	17,1	19,8	22,5	25,0	27,7

Погрешность определения температуры нагрева контактной системы АВ с I ном = 16 А соответствует диапазону от 0,3 до 47,5 %. Для АВ с I _ном = 32 А погрешность составила от 0,1 до 27,7 %. Для дальнейшего исследования параметров аппаратов используем данные, полученные с помощью компьютерной модели.

Моделирование потерь мощности и определение сопротивления контактов автоматических выключателей

Для исследования величины сопротивлений контактных соединений низковольтных аппаратов используются данные заводов-изготовителей по потерям активной мощности ∆ P на полюс аппарата. АВ, установленные на линиях цеховых сетей внутризаводских систем электроснабжения, предназначены для работы при длительном замкнутом состоянии контактов. Поэтому необходимо, чтобы аппараты работали при стабильном значении сопротивления контактов.

В разработанной компьютерной модели контактной системы АВ представлен блок расчета основных технических параметров АВ. Для удобства использования модели разработано приложение, позволяющее проводить запуск расчета перестроения геометрии модели, а также выводить графические зависимости. Предварительно в блоке задания параметров осуществляется ввод исходных данных. На рис. 6 и 7 представлены результаты исследования по разработанной программе.

Рис. 6 показывает, что при номинальной нагрузке для АВ с I ном = 16 А потери мощности не превышают 0,7 Вт, а для АВ с I _ном = 32 А – 1,55 Вт. Согласно ГОСТ 60898-1-2020⁷ максимально допустимое значение потерь мощности для АВ с I _ном = 16 А составляет 3,5 Вт, а для АВ с I _ном = 32 А – 4,5 Вт. Требование ГОСТ для исследуемых аппаратов выполняется на всем диапазоне коэффициента загрузки АВ от 0,1 до 1,2 I ном .

При изменении коэффициента загрузки от 0,1 до 1,2 для аппарата с I _ном = 16 А сопротивление контактов не превышает значения 2,9 мОм, а для АВ с I _ном = 32 А – 1,7 мОм.

’ Inputs
Шероховатость поверхности, неровности среднего наклона [Masp]: 0.4
Шероховатость поверхности, выступы средней высоты		[Qasp]:        1	um
Контактное нажатие [Р]:		1330	kPa
Рабочий ток [1г]:		16	A
Микротвердость [Нс]:		3	GPa
Коэффициент теплопередачи, [hk] [W/(m2*K)]:		5
	^St?	8® 0.85 |Ш| ^	IB Б
Потери мощности в контактном переходе	Surface loss density, electromagnetic (W)
	0.0038981
	^^t?	8® 0.85 Щ ®	В Б
Потери мощности на полюс	Volumetric i	oss density, electromagnetic (W)
	0.69398

^ H “ “ °-85 й ® ^ ^

Сопротивление                         „ г                                      Resistance (mu)

2.7266

Рис. 6. Рабочая область разработанного приложения для расчета технических параметров АВ с I ном = 16 А Fig. 6. Working area of the developed application for calculating the technical parameters of CB with I nom = 16 A

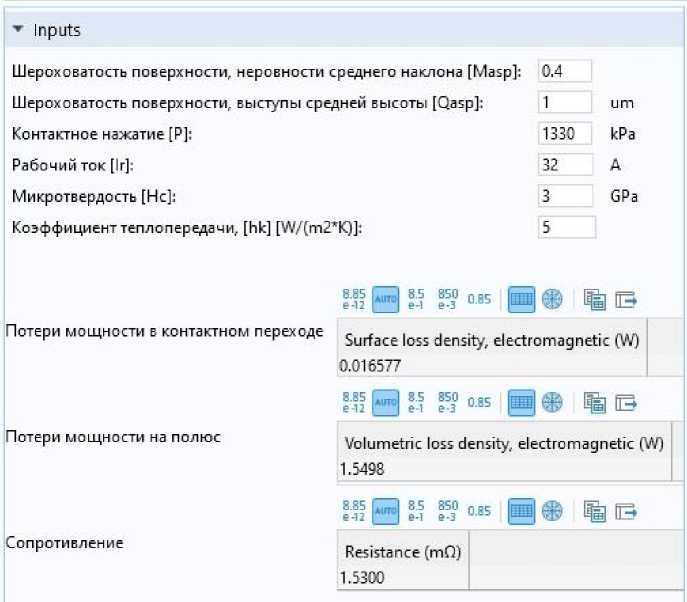
Рис. 7. Рабочая область разработанного приложения для расчета технических параметров АВ с I ном = 32 А Fig. 7. Working area of the developed application for calculating the technical parameters of CB with I nom = 32 A

Результаты моделирования сопротивления контактов ( R ) и потерь активной мощности (Δ P ) на полюс аппарата представлены в табл. 3.

Таблица 3. Результаты моделирования сопротивления контактов и потерь активной мощности на полюс аппарата

Table 3. Results of modeling contact resistance and active power losses per pole of the device

Тип аппарата		К з
		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2
АВ 16 А	Δ P мод , Вт	0,01	0,02	0,06	0,10	0,16	0,23	0,32	0,42	0,55	0,69	0,86	1,06
	R мод , мОм	2,41	2,42	2,43	2,45	2,48	2,51	2,55	2,60	2,66	2,73	2,80	2,90
АВ 32 А	Δ P мод , Вт	0,01	0,05	0,11	0,21	0,33	0,48	0,67	0,91	1,20	1,55	1,98	2,50
	R мод, мОм	1,23	1,24	1,25	1,27	1,29	1,32	1,36	1,41	1,46	1,53	1,61	1,71

В справочных и паспортных данных, как правило, отсутствует информация о потерях мощности в контактном переходе и на полюс низковольтных аппаратов, поэтому исследование законов изменения потерь мощности в контактах и контактных соединениях является актуальной задачей. В зависимости от номинального тока аппарата и его загрузки, потери мощности будут различными. Исследуем зависимости потерь мощности Δ P от номинального тока I _ном АВ

A P = F ( I ном ),                                              (2)

где F ( I _ном) – функциональные зависимости значений потерь активной мощности от величины номинального тока; I _ном – номинальный ток.

Для АВ функция аппроксимации значений потерь активной мощности на полюс аппарата имеет вид ( Петров и др., 2023б )

А Р ап =- 8 - IO " ⁵ • ( I _н • К з )² + 0,0673 - ( I н • К з ) + 0,3855, Вт.                         (3)

Для АВ с I ном = 16 А при К з = 1 потери мощности на полюс

А Р ^ 6 =" 8 - 10 —5 - 16 2 + 0,0673 - 16 + 0,3855 = 1,44 Вт.

Для АВ с I ном = 32 А при К з = 1 потери мощности на полюс

А Р_ап32 =— 8 - 10 — 5 • 32 2 + 0,0673 - 32 + 0,3855 = 2,46 Вт.

Результаты аппроксимации значений потерь активной мощности на полюс представлены в табл. 4.

Таблица 4. Результаты аппроксимации значений потерь активной мощности на полюс Table 4. The results of the approximation of the values of the active power loss to the pole

Тип аппарата		К з
		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2
АВ 16 А	Δ P ап16, Вт	0,49	0,60	0,71	0,81	0,92	1,02	1,13	1,23	1,34	1,44	1,55	1,65
АВ 32 А	Δ P ап32, Вт	0,60	0,81	1,02	1,23	1,44	1,65	1,85	2,06	2,26	2,46	2,66	2,85

Сравним значения функций аппроксимации значения потерь активной мощности на полюс аппарата с данными, полученными с помощью разработанной компьютерной модели. Результаты представлены на рис. 8 и 9.

На рис. 8 и 9: кривая 1 – график значений потерь Δ P мод по компьютерной модели (табл. 3), кривая 2 – график значений функции аппроксимации потерь (табл. 4) – Δ P _ап, прямая 3 – график допустимого значения потерь Δ P _доп согласно ГОСТ 60898-1-2020⁸.

Как показывают графические зависимости на рис. 8, для АВ с Iном = 16 А потери активной мощности на полюс, определенные с помощью компьютерной модели ΔPмод, и значения функции аппроксимации ΔPап не превышают значений, установленных ГОСТ 60898-1-2020, ΔPдоп = 3,5 Вт. Для АВ с Iном = 32 А (рис. 9) ΔPмод и ΔPап также не превышают допустимого значения ΔPдоп = 4,5 Вт. В качестве достоверных принимаем данные, полученные с помощью компьютерной модели, так как при моделировании учитываются параметры контактной системы для новых аппаратов, вводимых в эксплуатацию (рис. 6 и 7). При определении ΔPап исследованы аппараты, находящиеся в эксплуатации, параметры контактных систем которых отличаются от новых, а именно уменьшается контактное нажатие, увеличиваются шероховатости поверхностей материалов контактов.

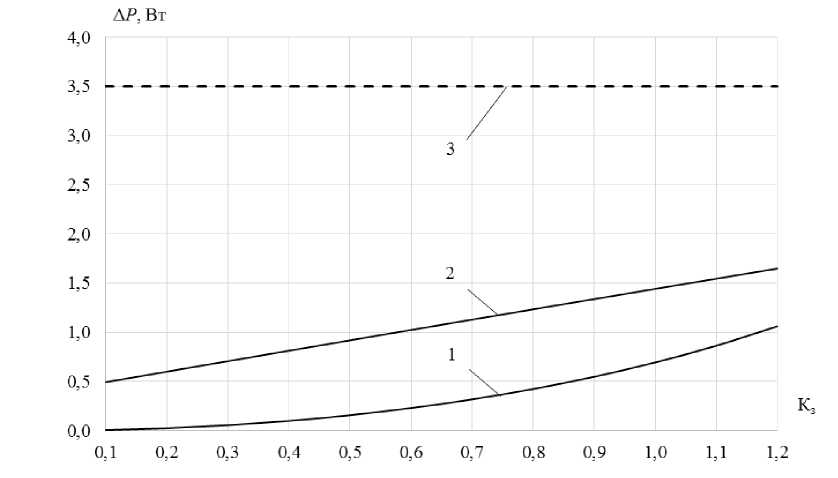
Рис. 8. Графические зависимости потерь активной мощности на полюс АВ I ном = 16 А от коэффициента загрузки аппарата

Fig. 8. Graphic dependences of active power losses per pole of CB I _nom = 16 A on the device load factor

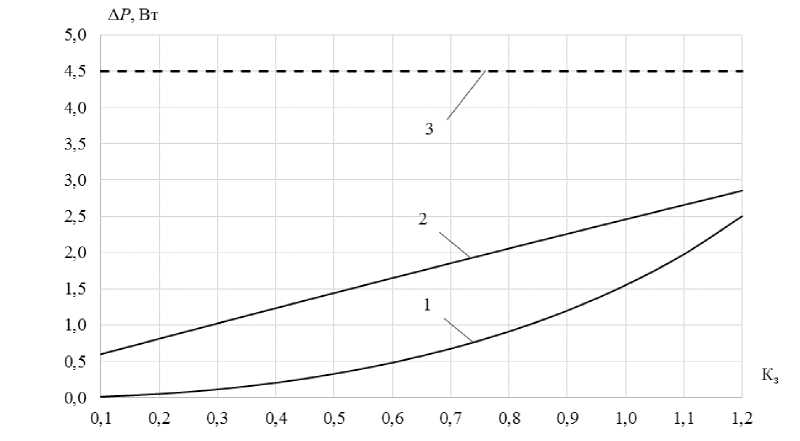
Рис. 9. Графические зависимости потерь активной мощности на полюс АВ I ном = 32 А от коэффициента загрузки аппарата

Fig. 9. Graphic dependences of active power losses per pole of CB I _nom = 32 A on the device load factor

Далее определим расчетным методом сопротивление контактных соединений исследуемых АВ

2 ^X- F ■ k _т ■ S ( I ном ■ К з )²

^t пр

( I ном ■ К з )² -Р-(1 + а- t расч ) F ■ k _т ■ S

, мОм,

где X - теплопроводность материала контактного соединения, Вт/(м ^ К); t _пер - допустимое превышение температуры контактного соединения АВ над температурой окружающей среды, °C.

Для АВ с Iном = 16 А при Кз = 1 сопротивление составит n 2 ■ 4390 ■ 2 ■ (3,0 + 1,25) 'Ю 3-16 • (3,0-1,25)-10-6)            162-1,7-10-8 • (1 + 0,0043 • 50,4)    ^

R =                                         - 65 -                                  = 4,76 мОм.

расч                                16²                              ^      2 - (3,0 + 1,25) - 10 ^{- 3} - 16 - (3,0 - 1,25) - 10 ^{- 6} J

Для АВ с I ном = 32 А при К з = 1 сопротивление составит

2 - 4 390 - 2 - (3,0 + 1,25) - 10 — 3 - 1" - (3,0 - 1,25) - 10 — 6 ) L      32 2 - 1,7 - 10 — 8 - (1 + 0,0043 - 86,9)     ^

R =                                         - 65 -                                  = 0,49 мОм.

32 2                              ^      2 - (3,0 + 1,25) - 10 ^{- 3} - 16 - (3,0 - 1,25) - 10 ^{- 6} J

Для определения сопротивления контактных соединений по потерям мощности используем выражение

А Р

R no _т=------о ■ , мОм.                                          (5)

( I ном - К з )²

Для АВ с I ном = 16 А при К з = 1 сопротивление R пот

Для АВ с I ном = 32 А при К з = 1 сопротивление R пот

R nom = 2F = 2,4, мОм.

В результате обработки экспериментальных данных сопротивлений контактных соединений АВ ( Петров и др., 2023а; Грачева и др., 2021; Абдуллазянов и др., 2021 ) получены следующие аппроксимирующие функции ( Петров и др., 2023а ):

• –    для АВ с I ном = 16 А

• Rэ кСП = 3,11- e 0,17Кз, мОм;                                             (6)

• –    для АВ с I ном = 32 А

• RЭкСп = 1,84 - e 0’29Кз, мОм.                                             (7)

На рис. 10 и 11 представлены графические зависимости результатов исследования сопротивлений контактных соединений АВ различными методами.

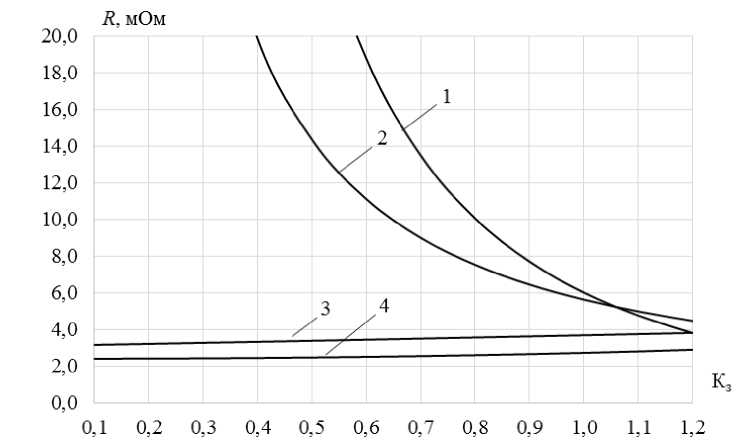
Рис. 10. Графические зависимости сопротивлений контактных соединений АВ I _ном = 16 А от коэффициента загрузки аппарата

Fig. 10. Graphic dependences of the resistance of contact connections of CB I nom = 16 A on the device load factor

На рис. 10 и 11: кривая 1 – график расчетных значений R _расч, кривая 2 – график значений R _пот по Δ P _ап, кривая 3 – график экспериментальных значений R _эксп, кривая 4 – график значений R _мод по компьютерной модели.

Графические зависимости на рис. 10 для АВ с I _ном = 16 А сопротивлений контактных соединений, определенных расчетным методом R _расч по выражению (4) и по потерям мощности R _пот по выражению (5), имеют похожий вид. При этом результаты значений R расч и R пот существенно расходятся с данными, полученными экспериментальным методом R _эксп. Графические зависимости сопротивлений, определенных с помощью компьютерной модели R _мод, имеют сопоставимые значения с экспериментальными данными R _эксп.

R, мОм

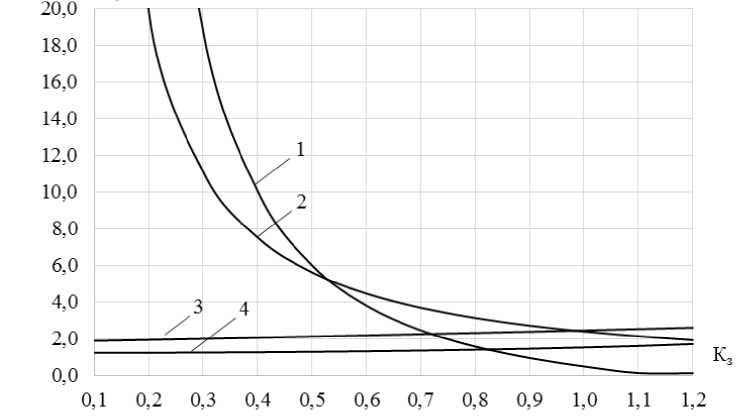
Рис. 11. Графические зависимости сопротивлений контактных соединений АВ I ном = 32 А от коэффициента загрузки аппарата

Fig. 11. Graphic dependences of the resistance of contact connections of CB I _nom = 32 A on the device load factor

Аналогичные результаты получены для АВ с I _ном = 32 А (рис. 11), где также наблюдается сопоставимость экспериментальных данных R _эксп и результатов расчета по компьютерной модели R _мод. Далее определим точность компьютерной модели при определении сопротивлений контактных соединений для исследуемых АВ (табл. 5 и 6).

В табл. 5 представлены результаты определения сопротивлений контактных соединений АВ различными методами – расчетным, по потерям мощности и экспериментальным.

Таблица 5. Результаты определения сопротивлений контактных соединений различными методами Table 5. The results of determining the resistance of contact connections by various methods

Тип аппарата	К з
	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2
R расч , мОм	715,08	177,94	78,47	43,65	27,53	18,78	13,49	10,06	7,71	6,02	4,77	3,81
АВ 16 А R пот , мОм	192,57	58,60	30,67	19,85	14,36	11,11	9,00	7,53	6,45	5,63	4,99	4,47
R эксп , мОм	3,16	3,22	3,27	3,33	3,39	3,44	3,50	3,56	3,62	3,69	3,75	3,81
R расч , мОм	177,94	43,65	18,78	10,06	6,02	3,81	2,47	1,58	0,96	0,50	0,14	0,13
АВ 32 А R пот , мОм	58,60	19,85	11,11	7,53	5,63	4,47	3,69	3,14	2,72	2,40	2,14	1,93
R эксп , мОм	1,89	1,95	2,01	2,07	2,13	2,19	2,25	2,32	2,39	2,46	2,53	2,61

Данные табл. 5 показывают, что соответствие R расч и R пот для АВ с I ном = 16 А наблюдается в диапазоне коэффициента загрузки аппарата от 0,7 до 1,2. Для АВ с I _ном = 32 А такое условие для R _расч и R _пот соответствует коэффициенту загрузки от 0,4 до 0,8. R _эксп для исследуемых аппаратов имеют сопоставимые значения с данными, полученными с помощью компьютерной модели R мод .

По результатам полученных данных предлагается рассмотреть возможность уточнения расчетного выражения (4) и выражения по потерям мощности (5) для определения сопротивления контактов, что позволит существенно сократить неточности и ошибки в вычислениях.

Для оценки точности результатов проведенных исследований сопротивлений контактных соединений АВ определим погрешность данных, полученных с помощью разработанной компьютерной модели относительно экспериментальных данных (табл. 6).

Таблица 6. Результаты расчета погрешностей при определении сопротивлений контактных соединений Table 6. Results of calculation of errors in determining the resistance of contact connections

Тип аппарата		К з
		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2
АВ 16 А	δ, %	23,9	24,9	25,7	26,4	26,8	27,1	27,1	27,0	26,6	26,0	25,2	24,0
АВ 32 А	δ, %	34,9	36,4	37,6	38,5	39,2	39,5	39,6	39,4	38,8	37,8	36,3	34,2

Погрешность при определении сопротивлений контактных соединений АВ с I _ном = 16 А соответствует диапазону от 23,9 до 27,1 %. Для АВ с I ном = 32 А погрешность составила от 34,2 до 39,6 %.

Заключение

В статье представлена разработанная компьютерная модель, которая позволяет проводить исследование основных технических параметров контактных систем АВ при изменении коэффициента загрузки аппарата. С помощью разработанной модели могут быть получены и исследованы следующие технические характеристики:  максимальная и минимальная температуры нагрева контактной системы аппарата, сопротивление контактных соединений и потери активной мощности на полюс аппарата. Для удобства применения модели и представления результатов моделирования разработано специальное пользовательское приложение. Результаты моделирования сопоставлены с требованиями соответствующих стандартов ГОСТ 60947-2-20219, ГОСТ 60898-1-202010 и ГОСТ 403-7311.

Сравнение полученных результатов моделирования параметров нагрева контактной системы с расчетными данными показало следующие погрешности для АВ с I ном = 16 А от 0,3 до 47,5 %; для АВ с I ном = 32 А – от 0,1 до 27,7 %. Полученные результаты моделирования сопоставимы с данными 28-суточных испытаний АВ. Поэтому возможно принять, что полученные данные соответствуют экспериментальным значениям нагрева контактных соединений АВ. Значения потерь мощности на полюс АВ при определении с помощью компьютерной модели и с помощью функции аппроксимации потерь мощности имеют сопоставимые значения и не превышают значений, регламентируемых ГОСТ. Значения сопротивлений контактных соединений, определяемые с помощью компьютерной модели, сопоставимы со значениями экспериментальных данных. При исследовании значений сопротивлений контактных соединений погрешность их определения для АВ с I _ном = 16 А составила 23,9 до 27,1 %, а для АВ с I _ном = 32 А – от 34,2 до 39,6 %.

Расхождение исследуемых данных по компьютерной модели от расчетных и экспериментальных значений объясняется тем, что при моделировании учитывались параметры контактной системы для новых аппаратов, вводимых в эксплуатацию. Принимая во внимание это допущение, можно утверждать, что разработанная модель адекватно описывает нагрев контактной системы АВ и позволяет определять основные технические параметры контактов аппарата: геометрические параметры контактной системы, допустимые значения контактного нажатия и шероховатостей материалов контактов. Компьютерная модель также позволяет производить расчеты и исследования при ухудшении параметров контактной системы в процессе эксплуатации. Под ухудшениями понимается изменение параметров геометрии контактной системы от проектных значений по причине сваривания и дребезга контактов, уменьшения значения контактного нажатия, увеличения значений шероховатостей материала контактов. Разработанная модель позволит контролировать техническое состояние исследуемых аппаратов в течение всего срока эксплуатации.