Применение регрессионного анализа данных при восстановлении крупногабаритного оборудования

Планирование эксперимента позволяет получить оптимальные значения выходных параметров при минимальном количестве опытов. В ходе проведения экспериментов необходимо исследовать влияние технологических параметров ротационного резца для обработки рабочей поверхности цапф мельниц при варьировании параметров.

Выходными параметрами для определения точности и качества обработанной цилиндрической поверхности цапфы мельницы с применением приставного станка, в условиях эксплуатации, выбраны – площадь срезаемого слоя S ср , мм² и шероховатость Ra, мкм.

В качестве основного плана для проведения эксперимента был выбран центральный композиционный ортогональный план полнофакторного эксперимента ПФЭ ЦКОП 24 [1]. Преимуществом данного плана является простота решения вычислений систем уравнения оценивания варьируемых параметров и избыточность количества измерений, уменьшающих влияние погрешностей измерений на оценку параметров обработки [2, 3].

В качестве факторов, определяющих воздействие на функции отклика, которые отвечают ряду предъявляемых требований: универсальности и возможности выражения в количественном виде выбраны: X i - передний угол у, град.; х - угол установки ш, град.; Х з - угол поворота р, град.; X - радиус режущей чашки резца г, мм.

Общее число опытов ЦКП при k факторов [2] составит

N = 2^k + 2k + m 0 , (1) где 2^k – число «звездных» точек; m 0 – число опытов в центре плана.

При составлении матрицы планирования эксперимента центральный композиционный ортогональный план предусматривает проведение только одного опыта, условия которого соответствует начальным значениям всех учитываемых факторов, т.е. m 0 = 1. Поэтому для ЦКОП выражение (1) примет вид:

N = 24 + 2 · 4 + 1=25. (2)

В соответствии с матрицей планирования ПФЭ ЦКОП 24 установлены уровни варьирования факторов: -1,414 и +1,414– звездные, -1 – нижний, 0 – средний, +1 – верхний. Уровни варьирования параметров приведены в таблице 1.

Таблица 1

Исследуемые факторы и уровни варьирования независимых переменных ПФЭ ЦКОП 24

Факторы	Кодированно е значение	Уровни варьирования
		-1,414	-1	0	+1	+1,414
передний угол γ, град.	х 1	16	24	44	64	70
угол установки ω, град.	х 2	0	5	16	25	30
угол поворота φ, град.	х 3	5	15	35	60	70
радиус режущей чашки резца r, мм	х 4	10	15	20	25	30

Влияние факторов на функции отклика может зависеть от уровня, на котором находится другой фактор, или от сочетания уровней нескольких факторов. Так как априорно не известно, что такой зависимости между факторами нет, построим развернутую матрицу планирования учитывающую не только факторы, но и их взаимодействия. При этом знаки в столбцах для взаимодействий получаем перемножением знаков взаимодействующих факторов (таблица 2). Последовательность опытов проводится случайным распределением, определяемым рандомизацией для исключения влияния систематических ошибок.

Таблица 2

Матрица планирования ПФЭ ЦКОП 24 и результаты эксперимента

№ п/п	х 1	х 2	х 3	х 4	Варьируемые параметры				Значения функции отклика
					γ (x 1 )	ω (x 2 )	φ (x 3 )	r (x 4 )	S ср , мм2	R a , мм
1	-	-	-	-	24	5	15	15	0,47	3,02×10-3
2	+	-	-	-	64	5	15	15	3,64	3,03×10-3
3	-	+	-	-	24	25	15	15	0,58	3,11×10-3
4	+	+	-	-	64	25	15	15	3,95	3,12×10-3
5	-	-	+	-	24	5	60	15	2,37	4,64×10-3
6	+	-	+	-	64	5	60	15	3,64	4,67×10-3
7	-	+	+	-	24	25	60	15	5,34	4,72×10-3
8	+	+	+	-	64	25	60	15	5,98	4,78×10-3
9	-	-	-	+	24	5	15	25	1,08	0,95×10-3
10	+	-	-	+	64	5	15	25	2,43	0,98×10-3
11	-	+	-	+	24	25	15	25	1,22	1,02×10-3
12	+	+	-	+	64	25	15	25	2,98	1,05×10-3
13	-	-	+	+	24	5	60	25	1,52	2,50×10-3
14	+	-	+	+	64	5	60	25	4,30	2,53×10-3
15	-	+	+	+	24	25	60	25	1,71	2,58×10-3
16	+	+	+	+	64	25	60	25	6,06	2,63×10-3
17	+1,414	0	0	0	70	16	35	20	3,96	2,35×10-3
18	-1,414	0	0	0	16	16	35	20	0,84	1,86×10-3
19	0	+1,414	0	0	44	30	35	20	3,33	2,14×10-3
20	0	-1,414	0	0	44	0	35	20	1,07	2,03×10-3
21	0	0	+1,414	0	44	16	70	20	2,48	3,72×10-3
22	0	0	-1,414	0	44	16	5	20	0,92	1,91×10-3
23	0	0	0	+1,414	44	16	35	30	2,91	1,32×10-3
24	0	0	0	-1,414	44	16	35	10	1,49	4,71×10-3
25	0	0	0	0	44	16	35	20	1,21	2,23×10-3

На основании экспериментальных данных были разработаны регрессионные модели, найдены коэффициенты уравнений регрессии произведена оценка их значимости, проверена адекватность регрессионных моделей [3].

Получено уравнение регрессии, характеризующее зависимость площади среза ^S ср от факторов варьирования γ, ω, φ, r в кодированной форме

S_cp = 0,12 + 0,11 x 1 + 0,06 x 1 + 0,025 x 1 x 2 + 0,03 x 1 x ₃ -L

• - 0,04 x 1 x ₄ + + 0,08 x 2 + 0,05 x 2 — 0,03 x 2 x ₃ + 0,045 x 2 x ₄ + L

+ 0,055 x ₃ + 0,025 x 2 ++ 0,011 x ₃ x 4 - 0,05 x ₄ + 0,05 x 2         (3)

Получено уравнение регрессии, характеризующее зависимость шероховатости обрабатываемой поверхности ^R a от факторов варьирования γ, ω, φ, r в кодированной форме

R a = 2,2 + 0,81 x 1 + 0,21 x 1 + 0,38 x 1 x 2 + 0,19 x 1 x ₃ -L

• - 0,31 x 1 x ₄ + 0,75 x 2 - 0,28 x 2 + 0,11 x ₂ x ₃ - 0,33 x ₂ x ₄ +L

+ 0,63 x з + 0,32 x 2 + 0,17 x ₃ x ₄ - 1,2 x ₄ + 0,43 x 4        (4)

Для детального исследования регрессионных моделей и определения

коэффициентов уравнений	регрессии в натуральных величинах,
кодированные значения	варьируемых    параметров     x 1 , x 2 , x 3 и x 4
целесообразно представить	в виде размерных величин γ, ω, φ, r.

Кодированные значения факторов ^x 1 ^{, x} 2 ^{, x} 3 ^{, x} 4 для натуральных значений

f x = ^ - 43 1     20 = a - 15 \ x = 2 - 38                                (5) 3    13 r - 20 x 4 = 7

Преобразовав выражение (1) в соответствии с (4), получаем уравнение регрессии для величины площади среза Sср , описывающее обработку цапфы, имеющей форму усеченного конуса, в натуральных величинах:

S_cp = 0,088 + 0,05 Y - 0,011 w - 0,049 Ф - 0,032 r +L + 0,00015 y ² + 0,00041 w ² + 0,00015 ф ² + 0,00102 r 2 -L - 0,000113 yw + 0,000115 YФ - 0,000286 Yr - 0,00021 аф +L + 0,00058 w - 0,00012 фг.

Определение значимости параметров для уравнения регрессии площади среза производится с помощью коэффициента эластичности показывающий степень количественного изменения одного фактора по отношению к другим

Э₁ =

a_i ∙ x_{i 0} a 0

где ^x i 0 – натуральное значение среднего уровня входного фактора; ^a 0 , ^a i – коэффициенты уравнения регрессии.

Значимость параметров определяется:

k = Э- 100% .                        (7)

ЭΣ

Для площади среза Sср a0=0,088 ;a 1=0,05 ;a2=0,011 ;a3 = 0,049; a4 = 0,032;

Э 1 = 24,4 ;Э 2 = 1,88 ;Э 3 = 21,16 ;Э 4 = 7,27 ;

k 1 = 44,6 % ; k ₂ = 3,4% ; k ₃ = 38,7% ; k ₄ = 13,3 % .

Полученные результаты представлены в виде диаграммы на рисунке 1.

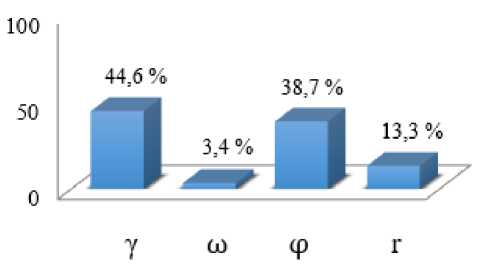
Рисунок 1 ˗ Диаграмма значимости параметров для площади среза

Анализ диаграммы показывает, что наиболее существенное влияние показателя на площадь среза оказывают передний угол γ (44,6 %) и угол поворота φ (38,7 %). Радиус режущей чашки r оказывает небольшое влияние (13,3 %), однако частично воздействует на величину площади среза. Влияние угла установки резца ω минимально (3,4 %).

Вышесказанное можно объяснить тем, что при увеличении переднего угла и угла поворота уменьшается деформация срезаемого слоя, силы резания и затрачиваемая мощность, при этом повышается качество поверхности, а условия схода стружки улучшаются, однако, чрезмерное увеличение – ослабляет режущее лезвие, увеличивает его износ вследствие выкрашивания и ухудшения теплоотвода.

Преобразовав выражение (2) в соответствии с (4), получаем уравнение регрессии для величины шероховатости поверхности R a описывающее обработку цапфы, имеющей форму усеченного конуса, в натуральных величинах

R_a = 9,34 - 0,014 y - 0,019 w - 0,176 ф - 0,434 r + L + 0,000525 y 2 + 0,00231 w ² + 0,00189 ф ² + 0,00878 r ² +L + 0,001727 yw + 0,000731 Yф - 0,002214 Yr + L + 0,000769 wф - 0,004285 wr + 0,001868 фг.

Определим значимость факторов для шероховатости по выражениям (6 – 7)

a ₀ = 9,34 ; a 1 = 0,014 ; a ₂ = 0,019 ; a ₃ = 0,176 ; a ₄ = 0,434 ;

Э 1 = 0,06 ; Э 2 = 0,03 ; Э ₃ = 0,72 ;Э 4 = 0,93 ;

$ 1 = 3,4% ;$ 2 = 1,7% ;$ ₃ = 41,4% ;$ ₄ = 53,5% .

Полученные результаты представлены в виде диаграммы на рисунке 2. В данном случае существенное влияние оказывают угол поворота φ (41,4 %) и радиус режущей чашки r (53,5 %). По сравнению с рассмотренным влиянием варьируемых факторов на площадь среза влияние переднего угла γ снизилось в десятки раз до 3,4 % и в 2 раза уменьшилось влияние угла установки резца ω (1,7 %).

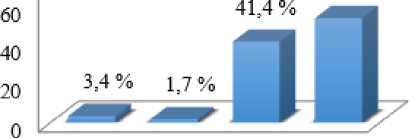
у со Ф г

Рисунок 2 ˗ Диаграмма значимости параметров для шероховатости

Полученные значения влияния объясняются тем, что увеличение радиуса закругления вершины резца способствует уменьшению высоты неровностей ˗ Ra шероховатости, при этом с увеличением угла поворота наклона оси уменьшается сход стружки, что также положительно влияет на качество обработанной поверхности.

На основании экспериментального исследования получены корреляционные уравнения регрессии, которые показывают зависимости площади срезаемого слоя и шероховатости поверхности цапф мельниц от исследуемых факторов: переднего угла, угла поворота, угла установки и радиуса режущей чаши. Произведена оценка значимости параметров регрессионной модели по критерию Стьюдента, по результатам которой определено существенное влияние переднего угла и угла поворота ротационного резца на величину площади среза, и радиуса режущей чаши с углом поворота резца на шероховатость.