Применение регуляризации к идентификации математической модели деструкции фенольных соединений в промышленных сточных водах по технологии Advanced oxidation processes

Сточные воды ряда отраслей промышленности (химической, фармацевтической, металлургической, целлюлозно-бумажной, горно-перерабатывающей и др.) вносят значительный вклад в загрязнение поверхностных и подземных водных объектов фенольными и трудноокисляемыми органическими соединениями. В технологических схемах очистки промышленных вод от фенольных соединений на многих предприятиях используется обработка стоков коагулянтами и флокулянтами. Однако эти методы имеют ряд недостатков, приводящих к повышенному образованию осадка и солесодержанию.

Современным и высокоэффективным методом удаления органических загрязнителей, содержащихся в промышленных сточных водах, яв-

ляются процессы, основанные на использовании свободных радикалов в качестве окислителей, использующие технологию усовершенствованных окислительных процессов (Advanced Oxidation Processes – АОР) [1]. Достоинством АОР-процессов является легкость регулирования их скорости в широких пределах с изменением интенсивности светового потока, быстрое и полное их приостановление с прекращением облучения.

Для управления процессом очистки сточных вод от фенольных соединений и идентификации математической модели на основе применения фотохимических методов при совместном действии окислителей перекиси водорода, хлорида железа (III) и ультрафиолетовго излучения длиной волны 365 нм проводились экспериментальные исследования с применением жидкостной и газовой хроматографии [2].

Управление процессами очистки сточных вод осуществляется на основе математических моделей, адекватно описывающих законы фотохимического разложения фенольных соединений в водной среде, представленные в зашифрованном виде экспериментальными данными. Для выявления этих законов и идентификации математических моделей применяется аппарат математической статистики, а именно регрессионный анализ, основанный на методе наименьших квадратов (МНК) [3]. Однако, алгебраическая задача МНК, применительно к оценке параметров математических моделей, описывающих процесс фотохимического разложения фенольных соединений в водной среде, является некорректно поставленной. Решение такой задачи может не существовать или не иметь единственного решения или может отсутствовать непрерывная зависимость решения от исходных данных, т.е. небольшим погрешностям исходных данных могут соответствовать существенные погрешности получаемых решений, что в конечном итоге приводит к неустойчивости оценок параметров идентифицируемой модели [4, 5]. Однако, при управлении процессом очистки сточных вод на стадии моделирования, варьированием уровнями факторов, необходимо получать адекватные прогнозные значения уровней остаточной концентрации фенольного соединения, содержащегося в воде по окончании очистки. Таким образом, целью работы является построение устойчивых решений при идентификации параметров математической модели, устанавливающей зависимость уровня снижения концентрации фенольных соединений в водной среде при воздействии фотохимических факторов.

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА

При проведении экспериментальных исследований, связанных с оценкой воздействия физико-химических факторов на уровень раз- ложения фенольных соединений в водной среде, в качестве зависимой переменной выбран показатель «содержание остаточной концентрации ВРА на выходе процесса». На уровень остаточной концентрации фенольного загрязнителя в процессе фотодеградации влияют следующие факторы: исходная концентрация ВРА в модельном растворе x1 – CBPA, мг/л; концентрация перекиси водорода x2 – CH2O2, мг/л; концентрация активатора, содержащего ионы железа (III) x3 – CA, г/л; время облучения x4 – t, ч.

При проведении опытных исследований каждый из факторов варьировался на двух уровнях – минимальном (кодированное значение – 1) и максимальном (кодированное значение +1). Границы пространства планирования заданы m-мерным кубом со сторонами – 1 ≤ xj ≤ +1, j = 1, 2, …, m [6]. Матрица планирования эксперимента приведена в табл. 1 [2].

МОДЕЛИРОВАНИЕИ ОБРАБОТКА РЕЗУЛЬТАТОВ

Будем считать, что влияние, оказываемое воздействием физико-химических факторов, на уровень снижения концентрации фенольного соединения в водной среде можно описать моделью вида [7]:

y = n + e = ^PJ_t ( x 1 ,x 2 , ^ , X m ) + £ , (1) i = 1

где: f_i(x₁, x₂,…, x_m) – произвольные функции факторов (регрессоров); в 1, в 2..., в k - коэффициенты

Таблица 1. Матрица полного факторного эксперимента

2 О	Планирование									Переменная состояния
	z 0	кодированный масштаб				натуральный масштаб
		z 1	z 2	z 3	z 4	x 1	x 2	x 3	x 4	y
1	+1	-1	-1	-1	-1	0,05	100	1	1	0,036
2	+1	+1	-1	-1	-1	0,1	100	1	1	0,071
3	+1	-1	+1	-1	-1	0,05	200	1	1	0,035
4	+1	+1	+1	-1	-1	0,1	200	1	1	0,068
5	+1	-1	-1	+1	-1	0,05	100	2	1	0,033
6	+1	+1	-1	+1	-1	0,1	100	2	1	0,064
7	+1	-1	+1	+1	-1	0,05	200	2	1	0,031
8	+1	+1	+1	+1	-1	0,1	200	2	1	0,061
9	+1	-1	-1	-1	+1	0,05	100	1	2	0,032
10	+1	+1	-1	-1	+1	0,1	100	1	2	0,062
11	+1	-1	+1	-1	+1	0,05	200	1	2	0,03
12	+1	+1	+1	-1	+1	0,1	200	1	2	0,059
13	+1	-1	-1	+1	+1	0,05	100	2	2	0,028
14	+1	+1	-1	+1	+1	0,1	100	2	2	0,056
15	+1	-1	+1	+1	+1	0,05	200	2	2	0,027
16	+1	+1	+1	+1	+1	0,1	200	2	2	0,053

модели; б - ошибка эксперимента.

Матрица регрессоров F (при планировании эксперимента F – расширенная матрица эксперимента) представляет собой следующую (N×k)

– матрицу:

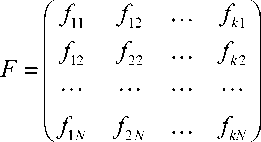
В каждой строке F записаны значения функций f_iu из модели (1) при данном наблюдении ( u = 1,2,…,N ), т.к. в регрессионном анализе предварительно предполагается некоторая структура модели, функции f_iu известны.

Исходя из закона действующих масс [8], которому подчиняется гомогенный фото-каталитический процесс разложения органических соединений, зависимость концентрации фенольного соединения от факторов процесса математически можно описать следующим выражением:

П = в 1 x \- x ^в x ^в x 4' , (2) где: п — уровень остаточной концентрации BPA в момент времени t, мг/л; x₁ – исходная концентрация ВРА, мг/л; x₂ – концентрация перекиси водорода, мг/л; x₃ – концентрация хлорида железа (III), г/л; х₄ - время процесса очистки, ч; Р 1 , Р₂, Р 3 , Р 4 , Р 5 - параметры модели.

Коэффициенты р в модель (2) входят нелинейно, но при линеаризации путем логарифмировании по натуральному основанию, правой и левой частей уравнения (2), получим:

~ ln Т~ = ln в1 + в2 ln~l + Р3 ln~2 + в4 ln~3 + в5 ln~4

, где в соответствии с (1): п = ln П, в = lnв1, fi =1, f> = ln xi, fз = ln x 2, ft = ln x з, f„ = f5 = ln x 4 .

Однако при таком преобразовании случайное возмущение (ошибка эксперимента) входит в модель мультипликативно и имеет логнормальное распределение, т.е. y = л ^е , и после логарифмирование это дает: ln y = ln ^ + In ^ [7].

После линеаризации и введении новых переменных, выражение (2) примет вид:

Y = b 0 + b 1 X 1 + b ₂ X ₂ + b ₃ X ₃ + b ₄ X ₄ , (3)

где: предикторные переменные X1, X2, X3, X4 и отклик Y являются логарифмическими функциями: Y = lny, X1 = lnx1, X2 = lnx2, X3 = lnx3, X4 = lnx4; b0, b1, b2, b3, b4 – параметры модели.

Обычно в задачах обработки данных матрица эксперимента и вектор отклика известны неточно, т.е. с погрешностями. Но даже при точно заданной входной матрице конечная разрядность ЭВМ, наличие ошибок округления и их накопление в процессе вычисления коэффициентов регрессии приводят к неопределенности представления матрицы эксперимента на этапах вы- числительной процедуры. Поэтому погрешности в матрице данных принципиально неустранимы, т.е. задача определения регрессионных коэффициентов по методу наименьших квадратов неустойчива к ошибкам в исходных данных [4].

Одно из основных предположений классической процедуры регрессионного анализа заключается в том, что матрица регрессоров F имеет полный ранг, а информационная матрица G = FTF – невырождена [7].

При вырожденности информационной матрицы нельзя вычислить коэффициенты регрессионной модели по формуле:

b = ( F T F )^{- 1} F T Y ,

поскольку не существует матрица C = ( F T F )* . Действительно, элементы матрицы С находят следующим образом:

^= ( - 1 1 j G " '!/ М .

Как известно, линейным преобразованием можно любую матрицу привести к диагональному виду. Пусть V будет ортогональной матрицей, столбцы которой – ортонормированные собственные векторы матрицы FTF, т.е.

(FV)T FV = VTFTFV = diag(X1,/2,_,Xk), где Х1, Х2, ^, Xk - собственные числа матрицы FTF.

Ортогональность матрицы V означает, что VTV = I и скалярное произведение любых двух столбцов матрицы V равно

1 при i = j , 0 при i ^ j .

k

VrV j = Y VV j, =\

1 = 1

Из линейной алгебры известно, что если X i

– собственное число FTF, то

FTFVi = XV, а также

I G =| f^tf| = X i , X 2 , ^ , X k .

Следовательно, информационная матрица G вырождена, если хотя бы одно из её собственных чисел X i равно нулю. Тогда выполняется условие

FTFVi = 0, что возможно только при FVi = 0, когда строки матрицы F ортогональны к Vi и существует зависимость:

V li f i + V 2 f 2 + - + Vf = 0 .     (5)

Уравнение (5) означает, что существует линейная зависимость между столбцами матрицы F, т.е. хотя бы один из них можно выразить как линейную комбинацию остальных. Если матрица FTF имеет p нулевых собственных чисел, существует p независимых между собой уравнений типа (5). Если столбцы матрицы F рассматривать как векторы, то p из них будут коллинеарны, т.е. будут иметь совпадающие направления. Такое явление называют строгой мультиколлинеарностью. Оно означает, что ранг матрицы FTF равен k – p (числу линейно независимых столбцов F). Иногда уравнение (5) выполняется лишь приблизительно. Это явление называется мультиколлинеарностью и имеет отрицательные последствия для оценивания регрессионных коэффициентов.

В случае мультиколлинеарности одно или несколько собственных чисел G = F^TF очень близки к нулю, поэтому близок к нулю и определитель информационной матрицы G . А так как обращение информационной матрицы связано с делением на G , который при сильной мультиколлинеарности будет очень малым числом, малые ошибки в вычислениях могут вызвать существенные различия в рассчитываемых элементах G = F^TF, а значит и в оцениваемых коэффициентах регрессии.

Отрицательные последствия мультиколлинеарности заключаются в неустойчивости оценок коэффициентов модели, численной неустойчивости процедуры оценивания, вызванной ошибками машинного округления и накоплением ошибок.

В линейной алгебре для исследования мультиколлинеарности прибегают к числам обусловленности. Для информационной матрицы плана G = F ^TF число обусловленности может быть определено как отношение максимального и минимального значений собственных чисел X, т.е. Р = Cond (F T F) = X_max / X_min. Чем больше число обусловленности, тем сильнее ошибка в исходных данных сказывается на решении линейной системы, т.е. число обусловленности характеризует точность решения [7].

Определяя в системе MathCad вектор собственных чисел информационной матрицы Фишера (F T F), получим: X{F T F} = (0,058; 526,312; 1,922; 1,922; 1,922); максимальное и минимальное собственные числа матрицы F^TF равны соответственно - X_max = 526,312; X_min = 0,0584. Число обусловленности информационной матрицы, в смысле евклидовой нормы, определенное через отношение собственных чисел составляет P(F^TF) = 9·10³. Сильная мультиколлинеарность проявляется при Cond (F^TF) ≥ 10⁵ – 10⁶ [7].

РЕГУЛЯРИЗАЦИЯ

Учитывая, что алгебраически задача определения оценок неизвестных параметров множественной линейной регрессии сводится к вычислению псевдорешений ф системы линейных алгебраических уравнений (СЛАУ):

А ф = f , (6) где: А е R m ^х " , m > n, rankA = n, ре R " , f e R m , то наиболее эффективным способом «борьбы» с мультиколлинеарностью является идея регуляризации псевдорешений, изложенная в работах А.Н. Тихонова [4, 5, 9, 10].

Согласно методу регуляризации А.Н. Тихонова, решение ф определяется из минимизации функционала

M [ф ] = |\фф - f ||2 + а||ф||2, то есть регуляризованное псевдорешение СЛАУ (6) определяется как решение задачи фа = arg min x е R"

{II ^{А ф -} f 112+ ^a ll ^p l 2 } },

где: ||*||2 - евклидова норма вектора; а - параметр регуляризации.

Решение регуляризованной задачи (7) эквивалентно решению системы уравнений:

(Ат А + al )фа = ATf, где: A – матрица СЛАУ; f – вектор-столбец правой части СЛАУ; Т – символ транспонированная; I – единичная матрица.

Регуляризация А.Н. Тихонова, в решении регрессионных задач, представляющая попытку преодолеть последствия плохой обусловленности матрицы (FTF), интерпретирована рядом исследователей как подход, названный гребневой регрессией (ридж-регрессией) [7, 11, 12].

Процедура построения гребневой регрессии, впервые предложенная в 1962 году А.Э. Хоэрлом, предназначена для работы в случаях, когда существование приближенных зависимостей между столбцами матрицы F приводит к тому, что матрица F^TF близка к вырожденной, из-за чего оценки параметров становятся неустойчивыми и, как правило, обладают большими стандартными ошибками. При использовании метода гребневой регрессии для стабилизации МНК-оценок, определяемых по формуле (4) при плохой обусловленности информационной матрицы, регуляризация связана с добавлением некого положительного числа т (параметра регуляризации) к диагональным элементам матрицы F^TF [11].

При условии выбора подходящего значения параметра регуляризации т, можно существенно уменьшить квадратичную ошибку МНК-оценок за счет их небольшого смещения. Выбор параметра регуляризации Хоэрл, Кеннард и Белдвин [11, 12] предложили осуществлять следующим образом:

m • 55_е     1

n - m - 1 ^ b*^Tb* ’

где: m – количество параметров (без учета свободного члена) в исходной модели регрессии; SS_e – остаточная сумма квадратов, полученная по исходной модели регрессии без корректировки на мультиколлинеарность; b^* – вектор-столбец коэффициентов регрессии, преобразованный по формуле:

b * = b j^( X j - X j ) •      (9)

где: bj – параметр при переменной Xj в исходной модели регрессии, определенный по МНК; Xj– среднее значение j-ой независимой переменной.

После выбора величины т формула для оценки регуляризованных параметров регрессии будет иметь вид:

b _T = ( F T F + t I )^- 1 F^TY ,        (10)

где: I – единичная матрица; F – матрица регрессоров; Y – вектор значений зависимой переменной.

Оценки параметров регрессии, полученные по формуле (10), будут смещенными. Однако, т.к. определитель матрицы (FTF+тI), больше определителя матрицы (FTF), дисперсия оценок параме- тров регрессии уменьшится, что положительно повлияет на прогнозные свойства модели [12].

В работах [7, 13] показано, что регуляризован- ные оценки можно записать еще и следующими двумя способами:

Ь =

— 1 —1

I + т(FTF)"   b = Zb ,

или bT = I — т( FtF + tI )

—i

b = ( I — t W ) b , (12)

где Z =

X — 1 ""I — 1                  ,     _               . — 1

I + t(FtF)    ,а W = (FTF + tI) .

Если рассматривать математическое ожидание обоих выражений (12), выясняется, что регуляризованные оценки оказываются смещенными и смещение их равно:

E (bT) — в = —t(FtF + tI)—1 в .   (13)

Очевидно, что смещение зависит как от параметра регуляризации т, так и от неизвестных значений регрессионных коэффициентов р.

За счет смещения можно достичь уменьшения квадратичной ошибки оценок М( т ) , которая разложима на две составляющие:

M ( т ) = f ( Ь т , — в , ) 2 = E ( b т — в ) ( b т — в ) = Y ( т ) + Y 2 ( т ) . (14) i = 1

Первая составляющая:

Y1 (t ) = а 2 Е( А/(А+ т )2),(15)

i=1 х'

где X i - собственные числа матрицы F T F . Она равна сумме дисперсий оценок коэффициентов.

Второй член

Y2 (т) = т2в (FTF + tI)—2 в = £[«.2 / ((А / т) +1)21, (16) г=1 LJ где: а = VP, а V- ортогональная матрица, столбцы которой – собственные векторы FTF. Тогда VTFTFV = Л, где Л - диагональная матрица с собственными числами на диагонали X1, X2, ^,Xk.

При сравнении (13) и (16), видно, что у2(т) равна квадрату смещения оценок регрессионных коэффициентов. Из (15) и (16) следует, что с ростом параметра регуляризации т сумма дис- персий оценок коэффициентов у1(т) монотонно убывает, в то время как квадрат смещения оценок монотонно возрастает. Очевидно, квадратичная ошибка оценки имеет минимум при у1(т) = у2(т), что видно из (14).

Доказано [13], что всегда существует такое значение т, при котором М(т) < M(0), M(0) – квадратичная ошибка, полученная МНК-оцениванием при т = 0.

Таким образом, при выборе подходящего значения параметра регуляризации, уменьшается квадратичная ошибка оценок [7].

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Для идентификации оценок коэффициентов регрессионной модели (3) по МНК в соответствии с формулой (4) использовались пакеты прикладных программ Statistica v.6.1 и MathCad 14.0. Анализ экспериментальных данных, проводимый в Statistica и MathCad позволил определить вектор коэффициентов модели bМНК = (–0,080788; 0,971642; –0,069869; –0,156662; –0,203063) и идентифицировать модель вида:

f—0,080788 + 0,971642ln CBPA — 0 C„s, = exp I ost (—0,156662ln CA — 0,203063ln t

, 069869 ln C _{H O}

¹² I ,(17)

где: Сост(t) и С0 – остаточная и начальная концентрации фенольного загрязнителя соответственно, мг/л; СH2O2 – концентрация перекиси водорода, мг/л; СА – концентрация хлорида железа (III), г/л; t – время, ч.

Значение коэффициента детерминации, близкого к единице (R²=0,999), показывает, что вариация факторов на 99,9% объясняет вариацию остаточной концентрации фенольного соединения при фотохимическом воздействии. Значимость коэффициента детерминации подтверждается с 99%-ной вероятностью (уровень значимости а=0,01) , в связи с тем, что критическое значение критерия Фишера F _kp со степенями свободы v 1 = 4, v₂ = 11 не превышает расчетного значения для регрессионной модели (F_кр(0,01;4,11)=5,67 < F=7292,13). На основе t-критерия Стьюдента установлена значимость оценок параметров модели (17) на уровне а =0,01, свободного члена на уровне а=0,05 (модули t-критерия t 1 =164,7; t₂=11,8; t₃=26,6; t₄=34,4 превышают критическое значение t(0,99;11)=2,72, а модуль t-критерия для свободного члена t₀=2,4>t(0,95;11)=1,79). О 99%-ной достоверности модели (17) экспериментальным данным свидетельствует принадлежность оценки дисперсии ошибок наблюдений 99%-ному доверительному интервалу (S²=6,7^10^-5 е (2,75^10 -5 ; 28,25·10^-5)). Статистика Дарбина-Уотсона DW=2,02 и сериальная корреляция остатков p_cor= -0,092, подтверждают высокую степень адекватности модели (17) результатам эксперимента [2].

Учитывая, что остаточная сумма квадратов в исходной модели регрессии (17) составляет

SS _e = 735,4402·10^–6 и квадратный корень из суммы квадратов ^ Х( X j - X j ) 2 = 1,3863 , то вектор преобразованных коэффициентов регрессии, определяемый по формуле (9), будет иметь вид b * = {1,346987; -0,096859; -0,217181; -0,281506} , j = 1,^ ,4. Величина параметра регуляризации, определяемая по формуле (8) будет иметь значение, равное т = 1,371^10 " ⁴.

Точность оценивания определяется по величине квадратичной ошибки оценки коэффициентов ( CKOK ˆ):

^k 2

CKOK = £ ( b i - b ) , i = 1

где: b ^ˆ _i – оценки значений коэффициентов модели, полученные методом регуляризации; b_i – значения коэффициентов модели, полученные по МНК.

Дополнительно к определенному по формуле (8) параметру регуляризации, зададимся рядом иных значений величины т. Результаты оценивания параметров модели (3) методом регуляризации при различных значениях т приведены в табл. 2.

Из табл. 2 видно, что наименьшая квадратичная ошибка оценок получается при т = 10^-5. Однако, при очень малых значениях параметра регуляризации её эффект незначителен, а при больших т влияние данных падает по сравнению с влиянием члена т I . Авторы работы [14] для того, чтобы не сильно «испортить» задачу, рекомендуют выбирать параметр регуляризации весьма малым, порядка 10^–3 – 10^–9.

Оценка параметра регуляризации т = 1,37Н0-4, принятая в соответствии с рекомендациями Хоэрла, Кеннарда и Белдвина [11, 12] дает приемлемый минимальный уровень квадратической ошибки, хотя это понятие субъективное [7], т.е. приемлемый выбор параметра регуляризации основывается на гребневом следе и варьируется в данном случае вокруг оптимального значения 1,371·10–4. При использовании пакетов прикладных программ Statistica и MathCad идентифицирован вектор регуляризированных оценок коэффициентов регрессии br = {0,081205; 0,971509; 0,069860; 0,156641; 0,203035}, и регуляризованная модель снижения концентрации фенольного соединения в виде:

<- 0,081205 + 0,971509ln C BPA - 0,06986ln C_HO

C_os, = exp l                                                    ²²

(- 0,156641ln C A - 0,203035ln t

, (18)

где: Сост(t) и С0 – остаточная и начальная концентрации фенольного загрязнителя соответственно, мг/л; СH2O2 – концентрация перекиси водорода, мг/л; СА – концентрация хлорида железа (III), г/л; t – время, ч.

Значение коэффициента детерминации, R² =0,9995, показывает, что вариация факторов при применении параметра регуляризации т на 99,95% объясняет вариацию остаточной концентрации фенольного соединения (ВРА) по модели (18). Значимость коэффициента детерминации подтверждается с 99%-ной вероятностью (уровень значимости а=0,01) , в связи с тем, что критическое значение критерия Фишера F_кр со степенями свободы v 1 = 4, v₂ = 11 не превышает расчетного значения для регуляризованной регрессионной модели (F_кр(0,01;4,11)=5,67 < F=5348,417). На основе t-критерия Стьюдента установлена значимость оценок регуляризованных параметров модели b jr на уровне а =0,01, свободного члена b_0r на уровне а =0,05. Уровни значений статистики t-критерия Стьюдента для регуляризованных параметров модели (18) со-

Таблица 2. Результаты оценивания параметров модели

S ч । си S Ч , ^ ° ^ ■в2 ® S i^ к си О'	b 1	b 2	b 3	b 4	CKOK ˆ
	0,971642	–0,069869	–0,156662	–0,203063	—
т = 1,37^10 1	0,971509	-0,069860	-0,156641	-0,203035	1,9·10-8
10–4	0,971545	-0,069862	-0,156647	-0,203043	1,008·10-8
2·10–4	0,971448	-0,069855	-0,156631	-0,203022	4,047·10-8
5·10–4	0,971157	-0,069834	-0,156584	-0,202961	2,529·10-7
10–5	0,971632	-0,069868	-0,156661	-0,203061	1,06·10-10
10–3	0,970672	-0,069799	-0,156506	-0,202860	1,011·10-6
1,836·10–3	0,969862	-0,069741	-0,156375	-0,202691	3,406·10-6
1,2·10–2	0,960121	-0,069041	-0,154805	-0,200655	1,427·10-4
1,7·10–2	0,955400	-0,068701	-0,154044	-0,199668	2,835·10-4
10–2	0,962022	-0,069177	-0,155111	-0,201052	9,947·10-5
1,55·10–1	0,841249	-0,060493	-0,135639	-0,175812	0,018
10–1	0,883311	-0,063517	-0,142420	-0,184603	8,386·10-3

ставляют: t{b_0r} = 2,0880; t{b_1r} = 141,0815; t{b_2r} = 10,1449; t{b_3r} = 22,7472; t{b_4r} = 29,4845. Модули значений t-критерия Стьюдента регуляризованных параметров b_jr превышают критическое значение t-критерия со степенью свободы v = 11 на уровне значимости a = 0,01 – t(0,99;11) = 2,72. Для свободного члена регуляризованной модели модуль расчетного значения t-критерия Стьюдента превышает критическое значение при уровне значимости а = 0,05 (|t{b_0r}| = 2,0880 > t(0,95;11) = 1,7959). Таким образом, регуляризованное значение оценки свободного члена, равное b_r0 = 0,081205 значимо на уровне а = 0,05. Стандартная ошибка оценки модели (18) составляет 0,00955; стандартная ошибка оценки свободного члена – 0,038892. Статистика Дарби-на-Уотсона DW=2,019 и сериальная корреляция остатков p c _or= -0,091273, подтверждают высокую степень адекватности регуляризованной модели (18) результатам эксперимента.

Доверительные интервалы для истинных значений параметров b _j множественной регрессионной модели в матричной форме имеют вид [15]: b j - t а ( N - m - 1 ) . I S ² (( F T F )^- ) <  b <  b j + t „ ( N - m - 1 ) - I S ² (( F T F ; ) , 12                      V '               i¹¹                    12                      ' '               i¹¹

j = 1,..., m , где: t a (N-m-1) - квантиль распределения Стьюдента порядка (1 - а/2) с (N - m - 1) степенями свободы; S2 ((FTF)_ I - оценка дисперсии ошибок наблюдений (осiтi аточная дисперсия);

T г'\

1 ( ^{F F} ) I - диагональный элемент корреляционной мат ⁱⁱ рицы; N – число наблюдений (строк матрицы планирования); m – число факторов модели; а - уровень значимости.

Учитывая, что корень квадратный из дисперсии есть стандартные отклонения оценок параметров регрессии b_j от истинных значений b_j, т.е. стандартные ошибки определения параметров регрессии b_j , то доверительный интервал упрощается к виду:

b j ± S { b j } - t _а ( N - m - 1 ) ,       (19)

где: S { b j } - стандартные ошибки отклонения МНК-оценок регрессии b_j от истинных значений b j ; t _a ( N - m - 1 ) - квантиль распределения 1

Стьюдента порядка (1 - а/2) с (N - m - 1) степенями свободы; N – число строк матрицы планирования; m – число параметров модели.

Вероятностным калькулятором системы Statistica при доверительной вероятности p = 1 - а = 0,95 (а = 0,05) определен квантиль распределения Стьюдента: t0,975(11) = 2,200985.

Доверительные интервалы (95%-ные) для истинных значений параметров регрессии b_j , построенные на основании МНК-оценок b_jМНК в соответствии с (19) имеют вид:

• •    для b₀:

  - 0,080788 ± 2,200985 - 0,0333 = ( - 0,154081; - 0,007495 ) ;

• •    для b₁:

0,971642 ± 2,200985 - 0,005898 = ( 0,958661;0,984623 ) ;

• •    для b₂:

• - 0,069869 ± 2,200985 - 0,005898 = ( - 0,082851; - 0,056888 ) ;

• для b3:

• - 0,156662 ± 2,200985 - 0,005898 = ( - 0,169643; - 0,143681 ) ;

• •    для b₄:

  - 0,203063 ± 2,200985 - 0,005898 = ( - 0,216044; - 0,190082 ) .

95%-ные доверительные интервалы для регуляризованных коэффициентов регрессии определялись в соответствии с формулой (19) с учетом того, что уровни стандартных ошибок отклонения регуляризированных оценок регрессии от истинных значений, оцененные в Statistica составляют: S{b0r} = 0,038896; S{b1r} = S{b2r} = S{b3r} = S{b4r} = 0,006887.

Доверительные интервалы для истинных значений параметров регрессии, построенные на основании регуляризованных оценок b_jr , принимают вид:

• •    для b₀(r):

  - 0,081206 ± 2,200985 - 0,038896 = ( - 0,166815;0,004403 ) ;

• •    для b₁(r):

0,971509 ± 2,200985 - 0,006887 = ( 0,956351;0,986667 ) ;

• •    для b₂ (r):

  - 0,069860 ± 2,200985 - 0,006887 = ( - 0,085018; - 0,054702 ) ;

• •    для b₃ (r):

• - 0,156641 ± 2,200985 - 0,006887 = ( - 0,171799; - 0,141483 ) ;

• для b4(r):

• - 0,203035 ± 2,200985 - 0,006887 = ( - 0,218193; - 0,187877 ) .

Область 95%-х доверительных интервалов для истинных оценок параметров модели, построенных на основе регуляризованных оценок коэффициентов регрессии b_jr пересекается с областью 95%-х доверительных интервалов, построенных для МНК-оценок коэффициентов, т.е. области доверительных интервалов являются смещенными, как и регуляризованные оценки параметров модели. Регуляризованные оценки являются значимыми, т.к. принадлежат 95%-м доверительным интервалам, построенным для значений этих коэффициентов.

ВЫВОДЫ

Обобщая приведенные выше результаты исследований, можно сделать вывод о том, что для идентифицированной по методу наименьших квадратов экспоненциальной модели снижения концентрации фенольных соединений в водной среде под действием физико-химических факторов проведена регуляризация, направленная на стабилизацию неустойчивых к ошибкам, ко- эффициентов модели. Регуляризованные оценки параметров модели получены методом гребневой регрессии с использованием приемлемого значения параметра регуляризации, выбранного способом, предложенным иностранными специалистами в области решения некорректных задач.

Полученная регуляризованная модель, устанавливающая зависимость степени разложения фенольных соединений в водной среде от параметров процесса (начальной концентрации фенольного соединения, концентрации перекиси водорода, концентрации хлорида железа (III), времени ультрафиолетового воздействия на систему) является статистически значимой и обладает лучшими прогнозными свойствами, чем исходная модель, идентифицированная по методу наименьших квадратов. Таким образом, регуляризованная модель фотохимического разложения фенольных соединений может давать более устойчивые прогнозные значения уровней содержания фенольных соединений в промышленных сточных водах на этапах планирования и проведения водоочистных мероприятий.