Применение схем расщепления потока ROE и AUSM в задачах сверхзвуковой аэродинамики

В задачах сверхзвуковой аэродинамики выбор метода расчёта численных потоков через грани ячеек в методах конечного объёма является важной темой исследований. Сверхзвуковые течения могут содержать газодинамические разрывы, что в свою очередь существенно осложняет численное моделирование. При этом численные схемы для аппроксимации конвективных потоков должны с достаточной точностью разрешать разрывы и сильные скачки уплотнения на небольшом числе ячеек с минимальными осцилляциями. Однако в работах [1-3] показано, что при использовании методов сквозного счета (shock capturing methods) возникают проблемы, связанные с правильным предсказанием сильных скачков уплотнения. Весьма популярной и хорошо себя зарекомендовавшей конечно-разностной схемой для решения задач сверхзвуковой газодинамики является схема Годунова [4], которая является монотонной и имеет первый порядок аппроксимации. В современных программных пакетах особой популярностью пользуется схема Роу [5]. Данная схема неплохо себя зарекомендовала при решении задач, где присутствуют контактные разрывы и ударные волны, однако имеет энтропийные проблемы [6], связанные с появлением нетипичных скачков [7]. Существует множество работ, исправляющих данный недостаток за счет методов корректировки энтропии, например [8-10]. Альтернативой методам расчета численных потоков на основе схем Годунова являются методы расщепления потока по схеме Ван Лира [11] или Лио и Стефана [12], причем последняя претерпела ряд модификаций [13-15] и получила название AUSM (Advection Upstream Splitting Method).

Схемы повышенного порядка аппроксимации позволяют уточнять решения как в области гладкого изменения газодинамических переменных, так и в области разрывов. Повышение порядка аппроксимации схемы можно достичь, заменив постоянное распределение газодинамических величин в каждой расчетной ячейке линейным [16] или параболическим [17]. Однако в местах разрывов может возникать неустойчивость. Чтобы решить данную проблему, В. П. Колган [18] первым предложил способ монотонизации решения, что реализовано в схеме MUSCL [19] (Monotone Upstream-Centered Schemes for Conservations Laws), в которой потоки вычисляются с использованием реконструированных значений переменных на гранях ячейки. Также существуют схемы с повышенным порядком точности, например схемы ENO [20] и WENO [21-22], однако они разрабатываются по большей части в собственных так называемых «іп-house» кодах в научно-исследовательских организациях.

Целью данной работы является верификация результатов, полученных с помощью программного пакета ANSYS FLUENT, и их сравнение с точным решением задачи о распаде произвольного разрыва в нестационарной постановке, а также рекомендации по применению схем ROE и AUSM в задачах сверхзвуковой аэродинамики.

2.    Анализ нестационарной задачи «ударной трубки», имеющей точное решение, с использованием схем расщепления потока ROE и AUSM

В данном разделе проведена процедура верификации двух схем расщепления потоков ROE EDS и AUSM с использованием первого, второго и третьего порядков аппроксимации. В качестве точного решения использовались данные, полученные из аналитического решения задачи о распаде произвольного разрыва в ударной трубке.

2.1.    Постановка задачи и ее аналитическое решение

Задача ударной трубки (shock tube problem) [23], закрытой с обоих концов и разделенной на две секции диафрагмой, является одной из разновидностей задач о распаде разрыва. Левая область содержит газ высокого давления, а правая область содержит газ при более низком давлении.

_u р\ _ / (1,0,¹⁰ ) , ⁽р,и,Г )    | ⁽₀.₀₁, о, 103) ,

0 < х <  5, 5 < х < 10.

После удаления диафрагмы образуется ударная волна (УВ), которая распространяется вправо. По мере движения УВ давление начинает расти, и индуцируется скорость в направлении УВ. Граница раздела - контактный разрыв (КР) между начальными состояниями газа также движется в направлении УВ с локальной скоростью газа. В то время как УВ движется вправо, волна разрежения (ВР) движется в противоположном направлении. Давление уменьшается как непрерывная функция через волну разрежения, и газ начинает течь вправо. На рис. 1 показано схематическое описание данного явления.

Рис. 1. Схематическое описание задачи об ударной трубке

					1 1
					।         ^ ц 1

Для заданных начальных условий для левой и правой частей трубки Андерсеном [24] получены точные решения для давления, скорости, числа Маха и плотности в момент времени t = 3.9 мс. Ударная волна расположена примерно на расстоянии 8.25 метра от левого конца трубки, ширина волны разрежения составляет примерно от 3.5 метров до 6.3 метров. Профили скорости и давления указывают на места расположения УВ и ВР. Профили числа Маха и плотности отображают воздействие на течение ударных волн и волн расширения, а также контактный разрыв.

Условия по всей ударной трубке аналитически определяются начальными состояниями газа в левой и правой частях трубки. Аналитическое решение рассматривается до тех пор, пока У В или ВР не отразятся от концов трубы.

2.2.    Численный метод и граничные условия

В качестве программы расчета для решения одномерной задачи об ударной трубке с невязким сжимаемым газом используется программный пакет ANSYS FLUENT [25] [26]. Данный код позволяет моделировать широкий класс процессов газовой динамики. Численно решается система уравнений Эйлера с помощью метода конечного объема со значениями переменных в центрах ячеек. Дискретизация конвективных потоков осуществляется с помощью схемы Roe FDS [5] либо с помощью схемы AUSM [12]. Вычисление градиентов производится методом Green-Gauss Node Based [26]. Пространственная аппроксимация выполнятся либо с первым, либо со вторым порядком точности, в том числе с использованием реконструкции MUSCL [19], которая имеет третий порядок точности в программном пакете ANSYS FLUENT. Дискретизация по времени осуществляется с помощью явного метода Рунге - Кутты четвертого порядка точности [26] с числом Куранта - Фридрихса - Леви CFL = 0.5 [23]. Задача решается в нестационарной постановке для идеального газа. Для сравнения численных результатов с аналитическим решением остановка расчета выполнялась в момент времени t = 3.9 мс.

Расчетная область была ограничена четырьмя стенками и центральной перегородкой. Инициализация полей в левой и в правой частях расчётной области осуществлялась согласно условиям (1) (см. рис. 2).

Static Pressure [ Ра ]

1.00е+03   1.09е+04  2.08е+04  3.07е+04   4.06е+04  5.05е+04   6.04е+04   7.03е+04  8.02е+04   9.01е+04  1.00е+05

Рис. 2. Начальные условия в правой и левой частях трубки

2.3.    Выбор расчетной сетки

Известно, что точность описания явления численными методами зависит как от используемого метода, с помощью которого решаются основные уравнения, так и от мощности сетки. Поскольку у разных методов существует различная зависимость получаемых результатов от степени подробности расчетной сетки, то перед основным циклом расчетных исследований необходимо провести серию дополнительных исследований по сеточной сходимости для используемого метода. Данный подход позволяет оценить, как уменьшение характерного размера ячейки расчётной сетки будет влиять на стремление полученных результатов к точному аналитическому решению (либо экспериментальному значению исследуемой величины или её метрики). В данной работе исследования сеточной сходимости проводились на семействе из трёх вложенных расчётных сеток с шагом дробления г = 4 (прореживание в 4 раза): подробная (fine) сетка имела 32 000 ячеек, средняя (medium) сетка имела 8 000 ячеек и грубая (coarse) сетка имела 2 000 ячеек. В качестве исследуемой величины была взята скорость распространения газа в трубке, а её метрики — отклонение расчетной величины от точного решения, которое вычислялось с помощью метрики [27], задаваемой формулой

1 Ү™'     ^(Хг ) - Y(Хг )

V = 1 - N Еth - Y(Х)    -                     (2> где у(хг) — расчетные значения скорости в точках хг для г = 1,2,... , N, a Y(хг) — значения, полученные из точного решения. Данная метрика нормализует расхождения между расчетом и точным решением.

В табл. 1 представлены значения метрики V в зависимости от количества ячеек для различных вариантов номинальных порядков аппроксимации по пространству, имеющихся в программном пакете ANSYS FLUENT. Видно, что для грубой сетки «coarse» метрика существенно отличается от метрики средней «medium» и подробной сетки «fine», а также от экстраполяции на бесконечно подробную сетку, рассчитанной по Ричардсону (см. рис. 3). Стоит отметить, что дробление сетки с шагом г = 2 (medium⁺ и тedium^-) также было исследовано и нанесено на график (см. рис. 3). При дальнейшем численном моделировании использована средняя (medium) сетка.

Таблица!

	100x20 = 2 000 ячеек (грубая — coarse)	400x20 = 8 000 ячеек (средняя — medium)	1 600 x 20 = 32 000 ячеек (подробная — fine)	Бесконечная сетка (экстраполяция по Ричардсону)	Пространственный порядок аппроксимации (Р)
Номинальный порядок аппроксимации 1	Уз = 0.9591	У2 = 0.9751	У1 = 0.9795	1 \ = 0.9813	0.931
Номинальный порядок аппроксимации 2	Уз = 0.9825	У2 = 0.9914	У1 = 0.9929	1 \ = 0.9939	1.284
Номинальный порядок аппроксимации 3	Уз = 0.9872	У2 = 0.9945	У1 = 0.9955	1 \ = 0.9956	1.433

В ходе проведения расчётов в рамках данной задачи была выявлена следующая особенность: сеточный порядок аппроксимации не совпадает с номинальным. Сеточный порядок точности вычисляется по формуле, представленной в работе [28], следующим образом:

ln

Р =

(

V 3 -V 2

V 2 -V 1

Zn ( r )

)

, где г - шаг дробления сетки, a V -значения метрики, полученные на раз

личных сетках.

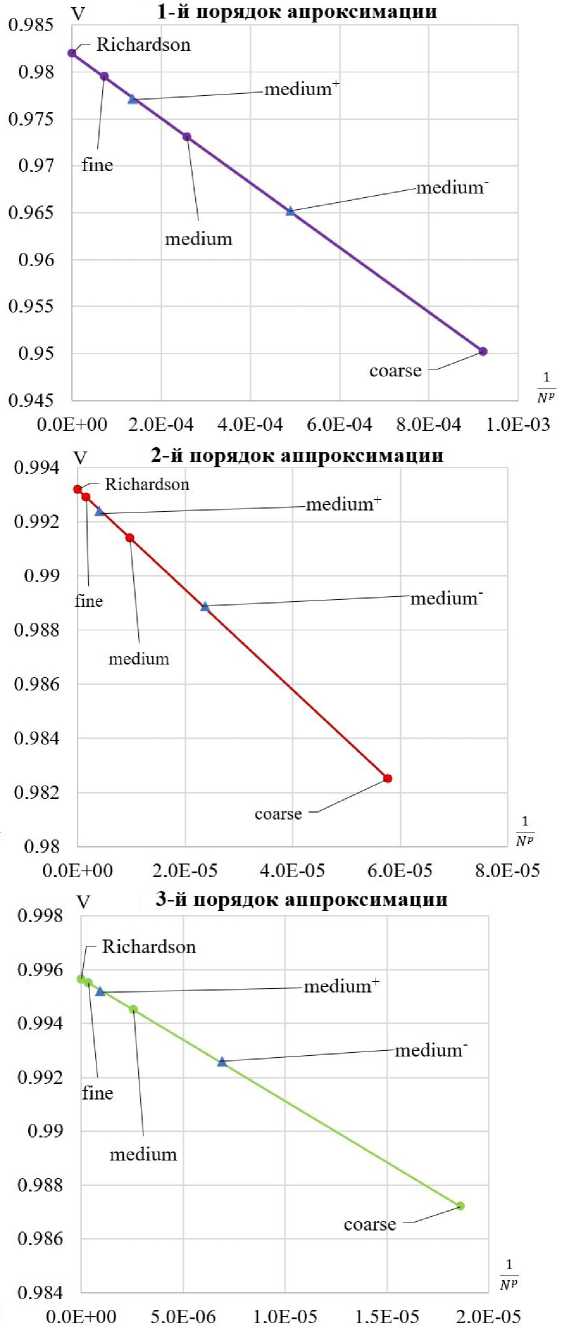
Рис. 3. Сеточная сходимость для схем трех поминальных порядков аппроксимации

Разница между теоретическим (математическим) порядком сходимости и реальным (сеточным) может быть связана с размером сетки, нелинейностями, возникающими в решении, присутствием ударных волн или волн разрежения. Например, по мгновенному распределению скорости в трубке в момент времени t = 3.9 мс можно увидеть особенности решения, возникающие в начале и в конце волны разрежения, а также на ударной волне в зависимости от размерности сетки (см. рис. 4).

С учётом того, что номинальный порядок аппроксимации может достигаться только в неразрывных решениях, а в местах разрывов точность снижается, согласно сделанным оценкам, сеточный порядок точности, полученный в данной работе, не превышает 1.5 (см. табл. 2).

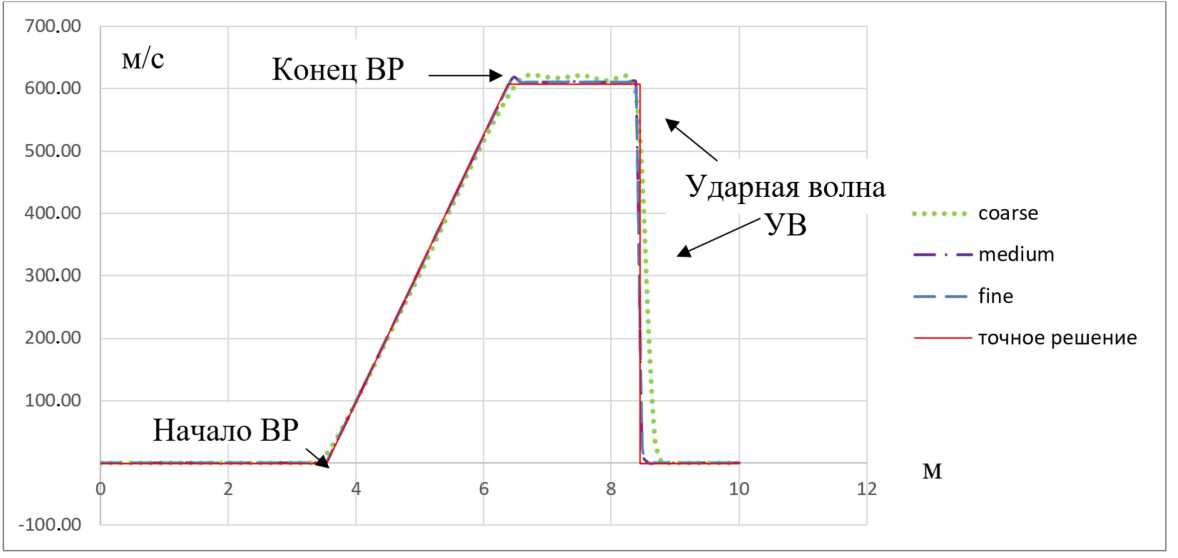
Рис. 4. Сравнение расчётных сеток по распределению скорости трубки в момент времени t = 3.9 мс

2.4.    Результаты расчётных исследований

Результаты с распределением плотности, числа Маха, давления и скорости по длине трубки при применении схем ROE FDS и AUSM с использованием первого порядка аппроксимации и их сравнение с точным решением [24] показаны на рис. 5. Видно, что в точке ж = 5 м наблюдается разрыв решения [23], так как в этой точке возникает звуковая скорость. В схемах первого порядка аппроксимации диссипация происходит в ударной волне, а также в начале и в конце волны разрежения. УВ «размазывается» на 4-5 ячеек, а контактные разрывы - на 6-7 ячеек. Несмотря на то, что схема первого порядка аппроксимации достаточно неплохо описывает профили давления и скорости (см. рис. 5), её диссипативность, т.е. искусственное сглаживание решения уравнения, может привести к неточному предсказанию взаимодействия скачка уплотнения с поверхностью, а также к неверному описанию взаимодействия пересекающихся скачков уплотнения. Это не позволяет применять данные схемы при решении аналогичных газодинамических задач сверхзвуковой аэродинамики с достаточной уверенностью.

Результаты решения задачи для второго порядка аппроксимации со схемами ROE EDS и AUSM приведены на рис. 6. Видно, что повышение порядка аппроксимации позволяет устранить разрыв параметров в области звуковой точки (см. рис. 6).

Сравнение этих результатов с точным решением и схемой первого порядка аппроксимации показывает, что диссипация уменьшилась в местах расположения УВ и волны разрежения (ВР). Однако, как видно из профиля скорости и числа Маха, теперь возникает небольшая числовая дисперсия в конце ВР. УВ «размазывается» на 2-3 ячейки, а контактный разрыв на 4-5 ячеек. По сравнению со схемой первого порядка аппроксимации видно, что схема более высокого порядка аппроксимации лучше предсказывает местоположение контактного разрыва, локализует волны разрежения и ударные волны.

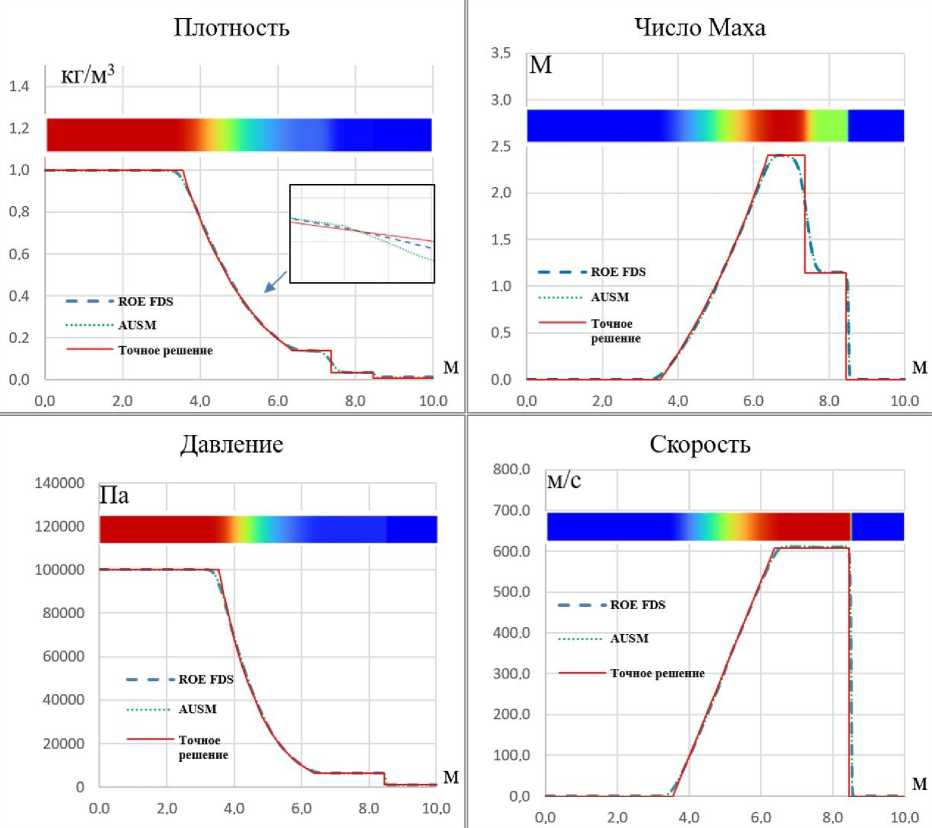
Рис. 5. Сравнение распределений плотности, числа. Маха, давления и скорости по длине трубки в момент времени t = 3.9 мс с точным решением для схемы первого порядка аппроксимации

Использование MUSCL подхода (для обеих схем ROE и AUSM) для повышения до 3-го порядков аппроксимации не дало существенных изменений по сравнению со вторым. Сравнение профилей плотности между схемами первого, второго и третьего порядков аппроксимации показывает, что методы более высокого порядка лучше фиксируют местоположение УВ и диапазон ВР. Схемы с использованием MUSCL подхода, могут более точно уловить место контактного разрыва, однако увеличение точности приводит к понижению устойчивости, иными словами уменьшение ошибок, связанных с диссипацией, приводит к увеличению ошибок, связанных с дисперсией. При повышении порядка, аппроксимации возникают колебания за. волной разрежения, на. контактном разрыве и перед ударной волной (см. рис. 7). Также стоит отметить, что проведенный анализ затраченного времени на. решение задачи с использованием MUSCL подхода увеличивает время расчета на 5-7% по сравнению с использованием других методов.

Как видно из графика, распределения скорости и плотности по длине трубки (см. рис. 6-7), дискретизация конвективных потоков методом ROE EDS и методом AUSM дают практически одинаковое численное решение как на. участке волны разрежения, так и в области контактного разрыва. Метрики данных методов практически совпадают, см. табл. 2.

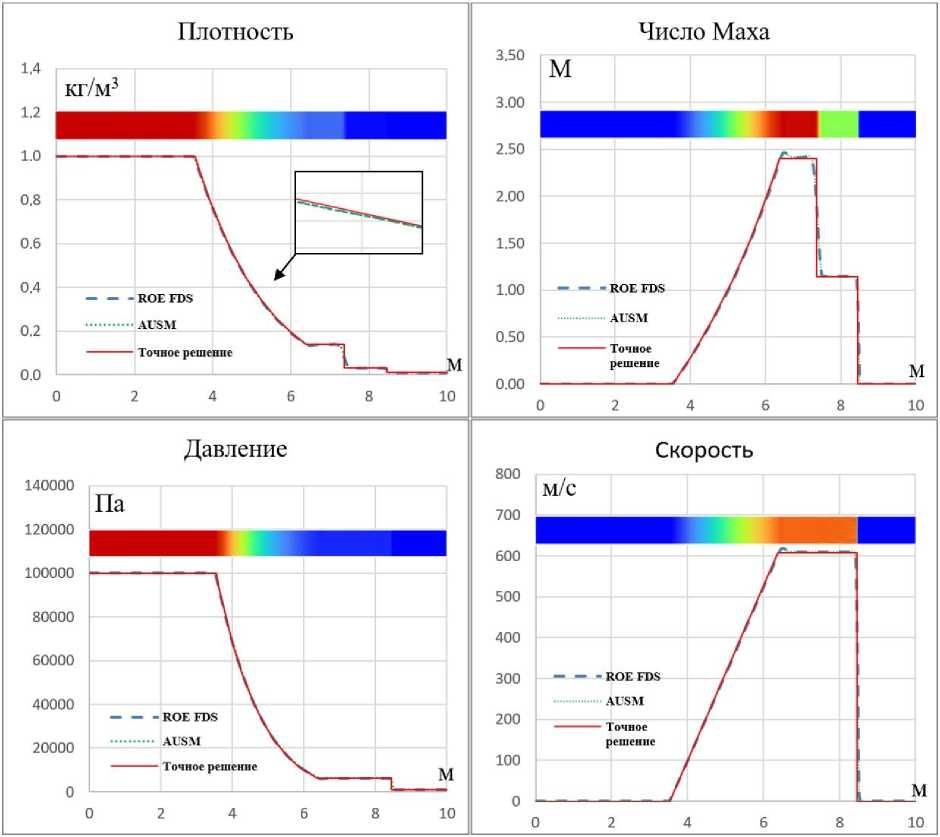
Рис. 6. Сравнение распределений плотности, числа. Маха, давления и скорости по длине трубки в момент времени t = 3.9 мс с точным решением для схемы второго порядка аппроксимации

Т а б л и ц а 2

	1-й порядок аппроксимации	2-й порядок аппроксимации	3-й порядок аппроксимации
V(ROE)	0 . 9751	0 . 9914	0 . 9945
V(AUSM)	0 . 9759	0 . 9923	0 . 9949

В заключение стоит отметить, что схемы первого порядка, аппроксимации обладают высокой диссипативностью с самой низкой метрикой для рассмотренной задачи: V = 0.9751-0.9759 (см. табл. 2). Схемы второго порядка аппроксимации могут точнее разрешить местоположение контактного разрыва, волны разрежения и ударной волны (метрика V = 0.9914-0.9923). Схемы третьего порядка аппроксимации с использованием MUSCL подхода увеличивают значение метрики до V = 0.9945-0.9949, фронт ударной волны становится менее пологим (см. рис. 8), однако время расчета увеличивается в среднем на 5-7%.

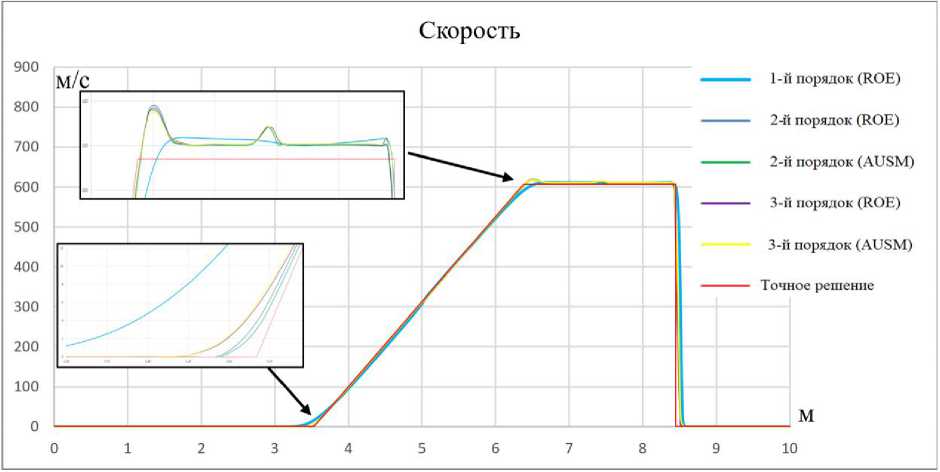
Рис. 7. Сравнение распределений скорости по длине трубки в момент времени t = 3.9 мс с точным решением для схем первого, второго и третьего (MUSCL подход) порядков аппроксимации

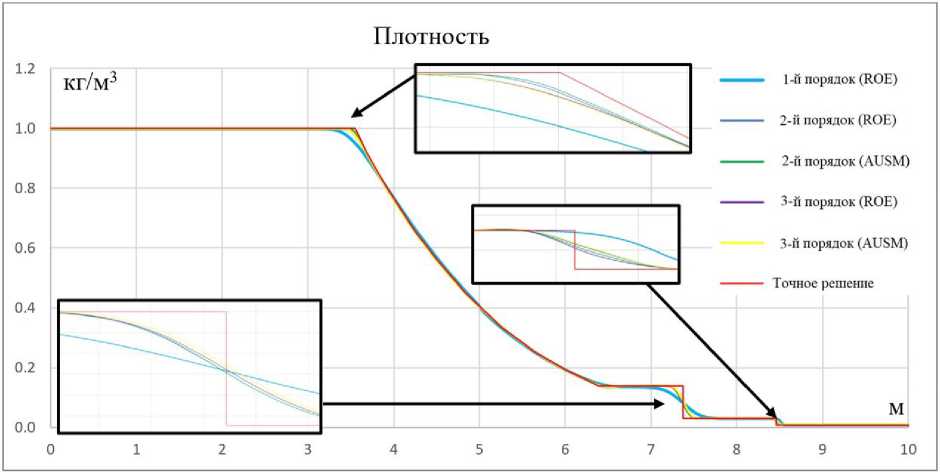
Рис. 8. Сравнение распределений плотности по длине трубки в момент времени t = 3.9 мс с точным решением для схем первого, второго и третьего (MUSCL подход) порядков аппроксимации

3.    Применение схем ROE и AUSM для решения задачи обтекания плоского сверхзвукового воздухозаборного устройства

Рассмотрим применение данных схем на практической задаче сверхзвуковой аэродинамики. В качестве предмета исследования была использована модель плоского одноступенчатого воздухозаборника смешанного сжатия со стеклянными боковыми стенками (см. рис. 9), предназначенными для визуализации течения внутри канала с помощью прибора Теплера. Модель ВЗУ также была оснащена приёмниками статического давления, которые были расположены на верхней и нижней стенках канала в плоскости симметрии ВЗУ.

Экспериментальные исследования были проведены в сверхзвуковой аэродинамической трубе RWTH Aachen University, Germany [29]. Параметры набегающего потока были еле- дующими: число Маха М^ = 2.41, угол атаки a = 10°, чиело Rex ю = 5.07 х 107 [1/м], полное давление Ро = 540 кПа и полная температура То = 305 К, входная турбулентность не превышала 1 %.

Рис. 9. Экспериментальная модель ВЗУ (из работы [29])

В работе [29] указано, что воздушный поток в плоскости симметрии плоского ВЗУ двумерный, что позволяет провести серию двумерных расчетов с использованием различных схем дискретизации конвективных потоков и номинальных порядков точности.

Численное моделирование проводилось путём решения системы осреднённых по Рейнольдсу уравнений Навье - Стокса с помощью метода конечного объема на двумерной сетке мощностью 791 х240 ячеек (см. рис. 10). В области пограничного слоя размер первой пристеночной ячейки по нормали к поверхности соответствовал величине у+ порядка 0.5. На задней границе канала ставилось граничное условие, соответствующее свободному протеканию потока. В качестве граничных условий для твердых стенок задавались условия непротекания и прилипания потока. Расчет выполнялся в стационарной постановке методом установления с числом Куранта - Фридрихса - Леви CFL = 1. При выполнении численного моделирования использовалась двухпараметрическая модель турбулентности к-ш SST [30].

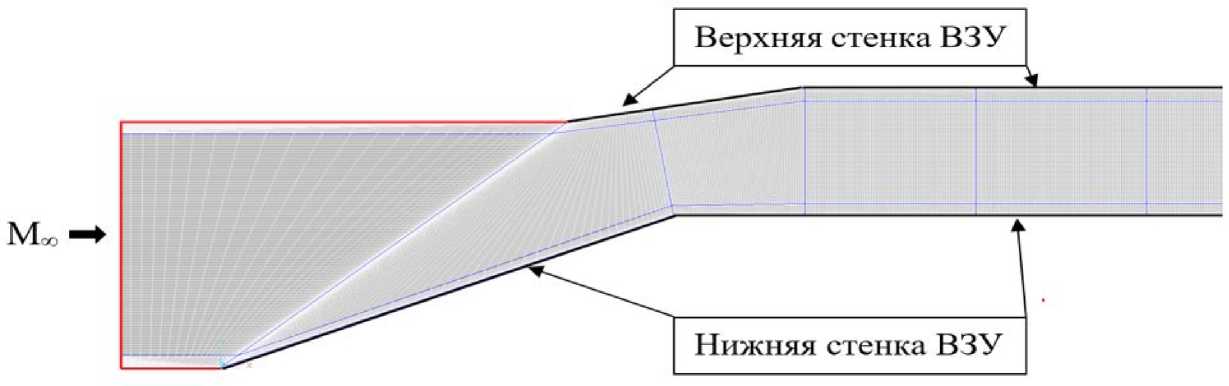
Рис. 10. Двумерная расчетная сетка для плоского ВЗУ

На рис. 11 представлено сравнение полей чисел Маха с использованием схемы НОЕ первого и второго порядка аппроксимации. Видно, что при использовании схемы первого порядка аппроксимации, из-за сильного «размазывания» разрывных решений, возникает некорректное предсказание взаимодействия скачка уплотнения с поверхностью нижней стенки ВЗУ, что приводит, как видно из рис. 12, к неправильному определению начальной точки отрыва пограничного слоя (ПС). Использование схемы AUSM с первым и вторым порядками аппроксимации дает аналогичные результаты.

На рис. 12 представлено сопоставление экспериментальных данных с расчётными результатами распределения статического давления по нижней стенке ВЗУ, отнесенного к полному давлению набегающего потока. Увеличение номинального порядка аппроксимации со второго на третий не приводит к существенному уточнению решения ни для одной из рассмотренных схем. Однако стоит отметить, что расхождение между экспериментальными данными и расчетными, как видно из рис. 12, может быть связано не только с выбором численной схемы, но и с выбором модели турбулентности, а также с тем, что был выполнен двумерный, а не трехмерный расчет, что в свою очередь явлется отдельной темой для дальнейших исследований.

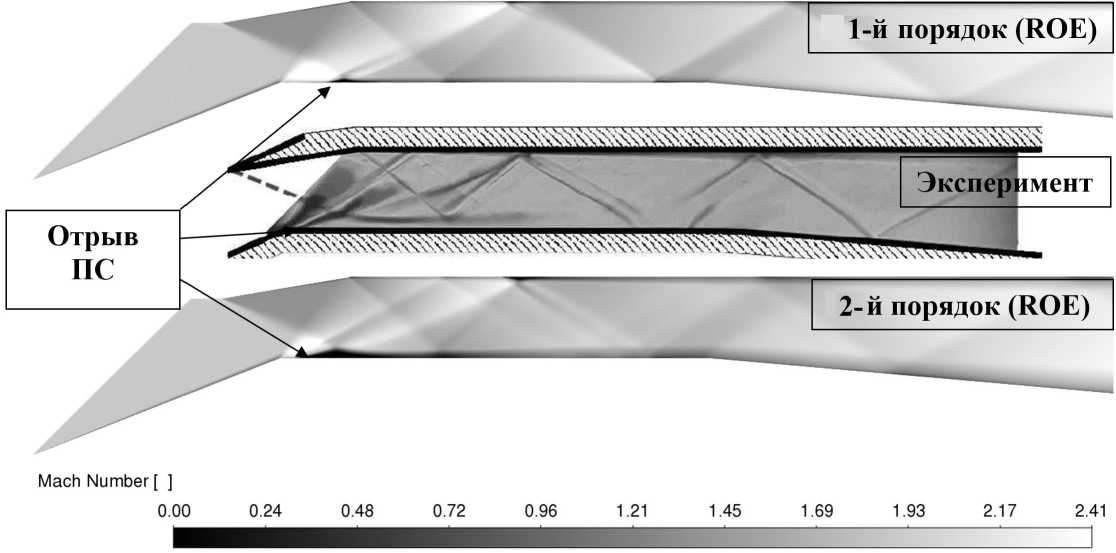
Рис. 11. Сравнение полей чисел Маха с использованием схемы ROE l-ro и 2-го порядков аппроксимации с экспериментальной картиной течения в канале ВЗУ

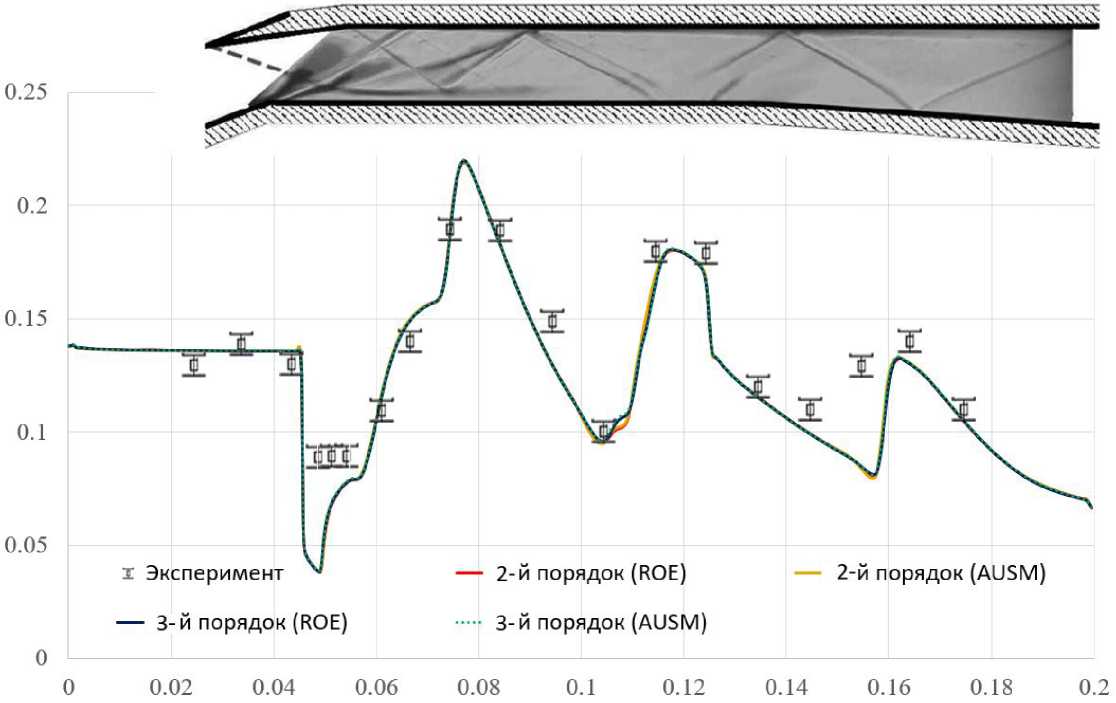
Рис. 12. Экспериментальные данные и расчётные результаты распределения относительного статического давления по нижней стенке канала ВЗУ на режиме полностью открытого дросселя

Также был проведен анализ затраченного времени на установление решения поставленной задачи. Этот вопрос является очень важным, потому что при проектировании ВЗУ рассматривается большое количество вариаций компоновки ВЗУ и планера летательного аппарата (например, вариации по высоте клина слива, расположению заборника относительно корпуса планера и т.д.). Для разработанных вариаций необходимо провести расчетные исследования в широком диапазоне чисел Маха, углов атаки и скольжения. В результате минимизация времени, затраченного на проведение расчётных исследований одной вариации, является очень важным аспектом в проектировании воздухозаборных устройств, так как позволяет в рамках ограниченных сроков проведения работ исследовать большее количество различных вариаций.

Так, в данной задаче на установление решения с использованием схемы НОЕ со 2-м порядком аппроксимации было затрачено времени на 5% меньше, чем с использованием 3-го порядка аппроксимации, на 4% времени меньше, чем с использованием схемы AUSM 2-го порядка аппроксимации, и на 9 % времени меньше, чем с использованием схемы AUSM 3-го порядка аппроксимации (см. рис. 13), при этом отклонение расчётных данных от экспериментальных значений для всех рассмотренных схем было практически одинаковым.

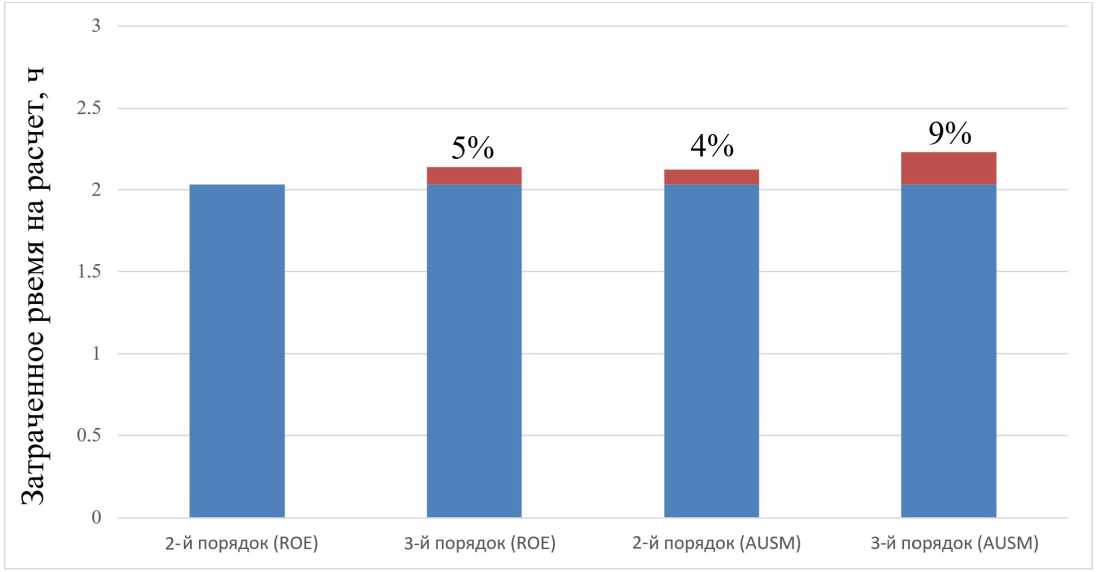
Рис. 13. Расчетное время для схем НОЕ и AUSM с использованием разных номинальных порядков аппроксимации

Таким образом, при параметрическом исследовании внутренних характеристик сверхзвуковых воздухозаборных устройств в расчётном пакете ANSYS FLUENT целесообразным является применение схемы НОЕ со вторым порядком аппроксимации при использовании модели турбулентности к-ш SST.

4.    Заключение

• 1.    На примере задачи о распаде произвольного разрыва параметров невязкого одномерного газового потока в нестационарной постановке в рамках верификации программного пакета ANSYS FLUENT (лицензия ЦАГРІ № 501024) проведено расчётно-методическое исследование с применением двух схем расщепления потока: ROE FDS (Roe Flux-Difference Splitting Scheme) и AUSM (Advection Upstream Splitting Method). Использованы схемы 1-го, 2-го и 3-го порядков аппроксимации.

• 2.    В качестве практического приложения рассмотрена задача обтекания плоского сверхзвукового воздухозаборного устройства (ВЗУ).

Исследована сеточная сходимость решения на семействе из трёх вложенных расчётных сеток с шагом дробления г = 4. Получено, что сеточный порядок точности, в отличие от номинального, не превышает 1.5.

Показано, что противопоточные схемы первого порядка аппроксимации «размазывают» решение для рассмотренного режима течения в месте расположения ударной волны на 4-5 ячеек, а в месте контактного разрыва - на 6-7 ячеек.

Использование схем 2-го и 3-го порядков аппроксимации позволяет более корректно предсказывать местоположение ударных волн, волн разрежения и контактных разрывов. При использовании этих схем ударная волна «размазывается» на 2-3 ячейки, а контактный разрыв - на 4-5 ячеек. Побочным эффектом данных схем является присутствие малых колебаний параметров в некоторых участках расчётной области, но их значения близки к точному решению. MUSCL подход лучше предсказывает место контактного разрыва, при этом время счета увеличивается на 5-7%. Дискретизация конвективных потоков методом ROE и методом AUSM дают практически одинаковое численное решение как на участке волны разрежения, так и в области контактного разрыва.

Показано, что применение схем ROE и AUSM 1-го порядка аппроксимации в задаче обтекания ВЗУ является нецелесообразным ввиду неточного определения начальной точки отрыва пограничного слоя на нижней стенке канала ВЗУ.

При параметрическом исследовании внутренних характеристик сверхзвуковых воздухозаборных устройств с применением расчётного пакета ANSYS FLUENT целесообразно использование схемы ROE со вторым порядком аппроксимации, так как данный подход дает преимущество по времени расчета одной задачи от 5 % до 9 % по сравнению с AUSM подходом второго и третьего порядков аппроксимации при практически одинаковом уровне погрешности численного решения.