Применение сингулярных последовательностей для моделирования трафика в сетях связи
Автор: Белоусов В.И., Линец Г.И., Михеев Ю.А., Фомин Л.А.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 1 т.7, 2009 года.
Бесплатный доступ
Предложен и обоснован метод формирования сингулярных импульсных последовательностей для моделирования самоподобного трафика в сетевых структурах, основанный на преобразовании функций случайных аргументов по произвольному закону.
Короткий адрес: https://sciup.org/140191294
IDR: 140191294 | УДК: 621.396.67
Текст научной статьи Применение сингулярных последовательностей для моделирования трафика в сетях связи
Для описания пульсирующей структуры или изменчивости (самоподобности) процессов и их количественной оценки обычно используют измеренные трафиковые трассы. Многочисленные публикации, связанные с трафиковым моделированием, основанные на реальных измерениях, преследуют цель проведения анализа на наличие, идентификацию и оценку количественных характеристик самоподобности, долговременной зависимости, а также для объяснения причин са-моподобности в сетевом трафике и исследования производительности сети при построении очередей [1]. Когда аналитический анализ невозможен, алгоритмы синтеза искусственных трасс чрезвычайно важны, поскольку их легко использовать при моделировании реакции сети на самоподобную нагрузку. Синтез искусственного трафика дает преимущества перед моделированием, использующим реальные (измеренные) трассы, по следующим причинам:
-
- трудность получения из реальных данных информации, необходимой для использования при моделировании параметров трафика (законы распределения, средние значения, показатель Херста, зависимость дисперсии от параметра агрегирования и др.);
-
- неудобство измерений и хранения реальных трасс в процессе моделирования;
-
- наличие нестационарности в измеренных (реальных) трассах может обмануть тесты на самоподобность – искусственный трафик этими недостатками не обладает;
-
- получение искусственного трафика с заданными свойствами не представляет особых проблем на этапе планирования эксперимента.
Реальные данные проявляют более сложную структурную зависимость, чем та, которую мож- но смоделировать с помощью специально сформированных процессов, обладающих долговременной зависимостью.
При пакетной коммутации непрерывный битовый поток с переменной скоростью передачи преобразуется в поток пакетов, при этом плотности распределения длительности интервала времени между поступающими пакетами однозначно определяют его статистические свойства и являются распределениями с «тяжелыми» хвостами [1]. Битовый поток со скоростью передачи r(t) поступает на вход элемента памяти, при этом длительность интервала времени г между пакетами определяется временем накопления информации в буфере, емкость которого достаточна для образования пакета заданной длины Lo (бит).
В [2] показано, что распределение длительности интервала при таком преобразовании определяется зависимостью
где f ( r ) – закон распределения скорости исходного битового потока.
Такая модель показывает, что распределение (1) приводит к появлению в потоке пакетов распределений с «тяжелыми» хвостами независимо от того, какой вид имеет исходный закон распределения битового потока. Сделан вывод о том, что в основе появления самоподобности в сетевом трафике пакетных сетей лежит один причинный фактор – процедура преобразования битового потока в поток пакетов.
Постановка задачи
Анализ показывает, что формула (1) справедлива в так называемом идеализированном окружении (неограниченные сетевые ресурсы и независимые источники трафика на всей сети). В реальных условиях это означает, что после буферизации каналы свободны, а возникающая задержка равна задержке пакетизации, которая и определяет характер распределения длительности интервалов между пакетами. При занятости канала сформированные пакеты могут находиться в памяти до освобождения канала (эффект состязаний), после чего могут передаваться подряд сразу несколько пакетов. Это приводит к возрастанию пачечности трафика и увеличивает «тяжесть» хвоста. К подобным эффектам могут приводить и некоторые механизмы управления трафиком, преимущественно с обратными связями (например, «оконное» управление на канальном и транс- портном уровнях, когда в зависимости от ширины окна, одновременно передается несколько пакетов, после чего возникает пауза, которая длится до появлении в узле-отправителе подтверждения). Благодаря этому случайная переменная т проявляет дополнительную изменчивость, при которой также увеличивается «тяжесть» хвоста. Выборки из такого распределения имеют очень маленькие значения т , но с конечной, и в общем случае не малой вероятностью, – очень большие значения т . В этом случае характер преобразования изменяется и не соответствует выражению (1).
Целью статьи является получение плотности распределения g (г ) при заданном законе распределения исходного битового потока f ( x ) и произвольном характере преобразования Т = ф ( х ) и исследование возможностей использования полученных результатов при моделировании самоподобного трафика в сетевых структурах.
Решение задачи
Подход, развиваемый в данной статье, связан с преобразованием функций случайного аргумента. Получаемый при этом процесс назван процессом с сингулярной (особой) интенсивностью.
Имеется случайная величина X с плотностью распределения f ( x ). Другая случайная величина т связана с ней функциональной зависимостью
Т = ф( x ). (2)
Необходимо определить плотность распределения величины .
Нахождение законов распределения функций случайных аргументов базируется на теории, изложенной в [3].
В данной статье рассматривается случай, когда исходная плотность вероятности f ( x ) описывает распределение мгновенных значений случайного процесса ^1( t ). С учетом этого уточнения, связь между мгновенными значениями случайного процесса и интервалом времени между образованными таким образом пакетами, перепишется в следующем виде:
V и )
G(r)= J/(x)A, (3)
где
V
q(r) = GV) = |
Решение (3) в общем виде базируется на использовании формулы Ньютона-Лейбница
|f(x) dx = F(x2 ) - F(xA \ (5)
С учетом (3) выражение (5) примет вид:
G(r) = F[^(r)]-F(a), откуда находим FMr)] = G(r)-F(«). Определим случайную величину T как r^-'^[GCV)-F(4
Учитывая, что \|/"‘ =ф, получаем r^{F-'[G(y)-F(a)]}, (6)
где величина а находится из условия нормировки V ( Г )
J g( г ) d г = 1 .
Импульсный поток с интервалами между поступающими импульсами, распределенному по закону (8), может быть получен путем нелинейных преобразований случайной величины. Иначе говоря, для генерации случайной величины с функцией распределения (6), необходимо построить детерминированную функциюr = G1(y)и получить искомые случайные числа как значения этой функции от аргумента, определяемого числом, являющимся случайной величиной с равномерным законом распределения на интервале (0,1).
Таким образом, перепишем формулу (6) с учетом этих соображений т = qAp"v\rnd - F(a)]} (7)
rnd – случайная переменная, равномерно распределенная в интервале (0,1).
Существует ряд алгоритмов для получения псевдослучайных чисел, например, метод вычетов. Если задать некоторое начальное число Yo в форме несократимой дроби Уо =mJM, где m0 и М – целые числа, и М – взаимно простое число с некоторым целым числом q, то все последующие числа /к будут несократимыми дробями У к = тк/М,где числитель mk определяется формулой тк+х =q-mk-A^-^-VM, (8)
М причем обратные квадратные скобки означают,что берется наибольшее целое число, не превышающее результат выполнения действий в скобках.Формула (10)является рекуррентной и позволяет получать последовательности псевдослучайных целых чисел, равномерно распределенных в интервале (1, M – 1).
Получаемые последовательности являются циклическими, так как через определенное количество шагов числа начинают повторяться. Удовлетворительная последовательность целых чисел получается с 17, я д ^*40
при q = 5 ; М = 2 , при этом длина неповторяющейся последовательности составляет 2,75·1011 чисел.
В качестве примера рассмотрим преобразование по формуле (6) двух исходных законов распределения: равномерного и экспоненциального. В качестве функции преобразования взята степенная функция х = кт”. Выбор таких функций преобразования для указанных законов распределения продиктован возможностью получения распределений длительности интервала между пакетами в виде распределений с заведомо тяжелыми хвостами: Парето (при а < 0) и Вейбулла (при а > 0).
Для распределения Парето интервал времени выражается зависимостью тп = к(Х - rnd) “ ,а<0.
Для распределения Вейбулла аналогичная зависимость имеет вид
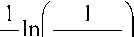
X \\-rnd J
Основываясь на исследованиях различных явлений, связанных с присутствием самоподобия, Херст разработал нормированную безразмерную меру, способную описать изменчивость этих явлений. Эта мера получила название нормированного размаха или R/S – статистики.
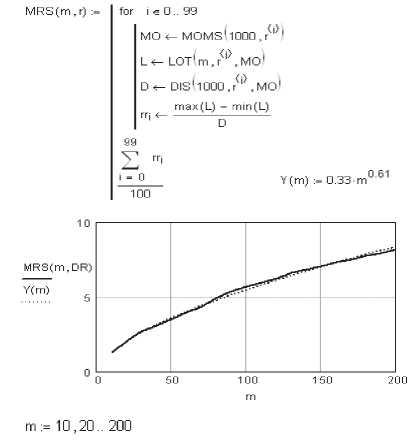
Для набора наблюдений X = ^хп, п G z} с — 1 ” ” выборочным средним x = fHXj вводится понятие размаха FG?) = max А - min А . , где А- __ ____ 1 ^k = ’^Xi - к х,Х/к = 1, и есть разность между максимальным и минимальным отклонениями. Характеристика размаха отличается от размаха временного ряда случайной величины х;., который равен max х,. - min х,. l Величина Rd>\ учитывающая накопление Aj и характеризующая изменчивость Xj относительно среднего значения, выбрана в качестве меры изменчивости процесса. Для описания изменчивости удобно использовать нормированную безразмерную характерис- R^ _ maxAy -minAy GRN(m) :- тику 5(и) 2 названную норми- рованным размахом, где ^^^Zk -xl – дисперсия исходного процесса. Оказалось, что для многих процессов, проте- кающих в природных условиях, справедливо эмпирическое соотношение при m —> oo, где с – эмпирическая константа. Логарифмируя обе части соотношения (9), получим loglfl/ n (n) ЭД. Hlogn + logC при m—> co. Метод R/S-статистики дает оценку только уровня самоподобности во временном ряде и позволяет получить лишь грубую оценку Н. Таким образом, этот метод, как и метод изменения дисперсии – лишь эвристические методы. Оба метода используются при различных ограничениях и слабо могут быть обоснованы при малом объеме статистических данных, доступных наблюдению на отдельных выборках заведомо самоподобных процессов. Ниже приведена методика получения самоподобной импульсной последовательности в соответствии с (7). Процесс реализован в среде Mahtcad 2001 Professional. Здесь же приведена реализация этого процесса из 1000 значений интервалов времени между импульсами, распределенных по закону Парето (R(1000)) и представлена методика оценки статистических свойств сформированной последовательности. На рис. 1 представлен график усредненного нормализованного размаха (10), который определяется по аппроксимирующей кривой (штриховая линия) у (m)-0,33 -m0161 где Н = 0,61 – показатель Херста последовательности R (1000). Заключение В настоящее время остро ощущается почти полное отсутствие теоретических результатов для долговременно зависимых моделей построения очередей. В этой связи особую актуальность приобретает возможность генерировать искусственные трассы в аспектах теории и практики построения очередей. Известно достаточное количество методов генерации искусственных трасс, for i e 0.. m - 1 Xj — rnd(1) N ;- GRN(1000) R(m) := M for GRN (m) i € 0 .. last(N) (1 - N|i 2 MOMS(m,r) := for i e 0.. 0 LOS o return LOS MO .= MOM3(1000,R(1000)) MO - 2.088 D := DIS (10ОО , R (1000) , M О MS (1000, R (1000))) D = 9.706 DR := fur i e 0 .. 100 r{l> ^ R(1000) R(1000) - 0 0 1 .025 1 1.064 2 1.961 3 1 .002 4 4.79 5 2.003 6 1.763 7 1.723 8 1.038 9 2.685 10 3.001 11 1.086 1 2 1 .532 Рис. 1. Усредненный нормированный размах хотя точные методы, как правило, не реализуются для длинных временных рядов. Кроме того, их быстродействие оставляет желать лучшего, а статистические свойства их до настоящего времени не достаточно изучены. Предлагаемый в данной статье метод генерации искусственного трафика позволяет подобрать функцию преобразования ^ (х) и, зная исходный закон распределения f(x) смоделировать любой процесс q(' ) с заданными свойствами.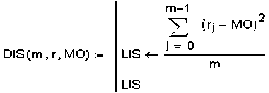
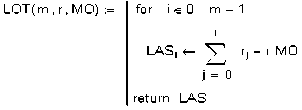
Список литературы Применение сингулярных последовательностей для моделирования трафика в сетях связи
- Турко С.А., Фомин Л.А., Будко П.А. Об оптимальном использовании сглаживающего влияния буферов на параметры трафика//Электросвязь. 2002. № 10. С. 26-29.
- Шелухин О.И., Тенякшев А.М., Осин А.В. Фрактальные процессы в телекоммуникациях. М.: Радиотехника, 2003. 408 с.
- Вентцель Е.С. Теория вероятностей. М.: Асадема, 2003. 571 с.


