Применение системы автоматического проектирования Ansys Maxwell для количественной оценки влияния эффекта вытеснения тока в электрических машинах переменного тока

В настоящее время проектирование электрических машин достаточно автоматизировано. Связано это с ростом промышленных мощностей и конкуренцией на рынке. Проектирование требуется производить быстро и точно, с минимальными погрешностями.

На АО «НПО «Электромашина» был разработан генератор переменного тока, работающий в паре с выпрямителем, номинальной мощностью 1000 кВт. Краткие характеристики проектируемого генератора приведены в таблице.

Машина подобного рода обладает следующими основными видами потерь [1]:

• -    магнитные потери на перемагничивание, гистерезис и вихревые токи в стали статора;

• -    электрические потери в обмотке статора, вызванные протеканием тока нагрузки.

Остальные потери, такие как: поверхностные потери в постоянных магнитах вследствие зубцо-вости статора, механические потери в подшипниках, потери на трение ротора о воздух и т. д., в данной статье будут опущены, ввиду их малой величины в сравнении с основными потерями и небольшого влияния на суммарный КПД электрической машины [2, 3].

Электромагнитный расчет производился двумя методами. По классическим методикам, с ис-

Краткие характеристики проектируемого генератора

Параметр Номинальная выходная электрическая мощность (после выпрямителя) Номинальный ток нагрузки (после выпрямителя) Частота вращения вала генератора Номинальное напряжение постоянного тока (после выпрямителя) Напряжение холостого хода, не более Ед. изм. кВт А Об/мин В В Знач. 1000 1100 2100 900 1200 пользованием пакета Mathcad на основе методической литературы [4]. И методом конечных элементов с использованием пакета ANSYS Maxwell.

Согласно проведенным расчетам, КПД полученного генератора составляет 97 %. Из 30 кВт суммарных основных потерь (без учета эффекта вытеснения тока) 15 кВт потерь, по расчетам, составляют магнитные, и 15 кВт составляют электрические потери. Полученный результат соответствует условию работы машины с максимальным КПД, как показано ниже.

Условие работы электрической машиныс максимальным КПД

Запишем коэффициент полезного действия через коэффициент нагрузки:

нг   кнгР2н + Рмаг + кНгРэл ’ где кнг = Р2 (Рн^ - коэффициент нагрузки электрической машины (при неизменном напряжении то же, что отношение текущей токовой нагрузки к номинальной, то есть кнг = I2 /12н );

P _2н – номинальная выходная мощность (прямо пропорциональна коэффициенту нагрузки, так как мощность от тока зависит практически линейно);

P _маг – магнитные потери при номинальной нагрузке (от тока практически не зависят, поэтому множитель отсутствует);

P _эл – электрические потери при номинальной нагрузке (зависят от тока нагрузки во второй степени, поэтому множитель во второй степени).

Условием максимума функции коэффициента полезного действия электрической машины является равенство нулю производной данной функции [5, 6].

Запишем производную функции КПД и определим условие равенства ее нулю:

п "^к-) =

^Р 2н ( к нг ^Р 2н ^{+ Р} Маг ⁺ к нг ^Р л ) ^- к нг ^Р н ( ^Р н ^{+ 2к} нг ^Р л ) =      ----------;-------------- .⁽²⁾

( к нг ^р 2н ⁺ P Map ⁺ к нг ^р эл )

Из условия равенства производной нулю, получаем:

• ^Р 2н ( ^к нг ^Р 2н ^{+ Р} маг ⁺ к нг ^Р эл ) ^-

• — к нг Р 2н ( Р 2н + 2к нг Р эл ) = 0;                (3)

• 9 Р .

• к 2г = ^Р м^а^ .                                    (4)

P эл

Следовательно, при номинальной нагрузке, когда коэффициент нагрузки равен единице, условием максимума КПД будет являться равенство магнитных и электрических потерь. Строго говоря, в общем виде зависимость КПД от коэффициента нагрузки является более сложной, однако было оговорено принимать в расчет лишь основные (существенно влияющие на КПД) потери электрической машины (электрические и магнитные).

Таким образом, рассчитанный генератор имеет максимальный КПД 97 % в точке, соответствующей номинальной мощности.

С целью проверки расчетов на наличие грубых ошибок проводится моделирование работы проектируемого изделия в среде ANSYS Maxwell.

Моделирование работы генераторав ANSYS Maxwell

При расчете генератора в пакете ANSYS Maxwell была создана двухмерная модель генератора (разрез поперек оси вала), скриншот из программы представлен на рис. 1.

Магниты в модели намагничиваются по осям относительных систем координат, которые создаются отдельно для каждого магнита и вращаются вместе с ротором. Обмотка в модели соединяется в катушки, а катушки в фазы [7, 8].

Фазы обмотки соединены в многоугольник и подключены к девятифазному мостовому двух-полупериодному выпрямителю, как показано на рис. 2. В схему также подключены элементы, обозначающие активные сопротивления и индуктивности рассеяния лобовых частей обмотки, которые можно получить из расчета электрической машины в подпрограмме RMxprt Desing или ориентировочным расчетом с применением стандартных методик [9, 10].

В процессе моделирования работы генератора в пакете ANSYS Maxwell сначала была рассмотрена работа генератора в режиме холостого хода [11, 12]. Так как генератор магнитоэлектрический, для регулирования напряжения на выходе генератора необходимо изменять частоту вращения его вала. В связи с этим имеет смысл провести расчет выходного напряжения генератора при холодных магнитах (20 °С) и при нагретых. Осциллограмма напряжения при работе с холодными магнитами показана на рис. 3. Было получено значение 1130 В.

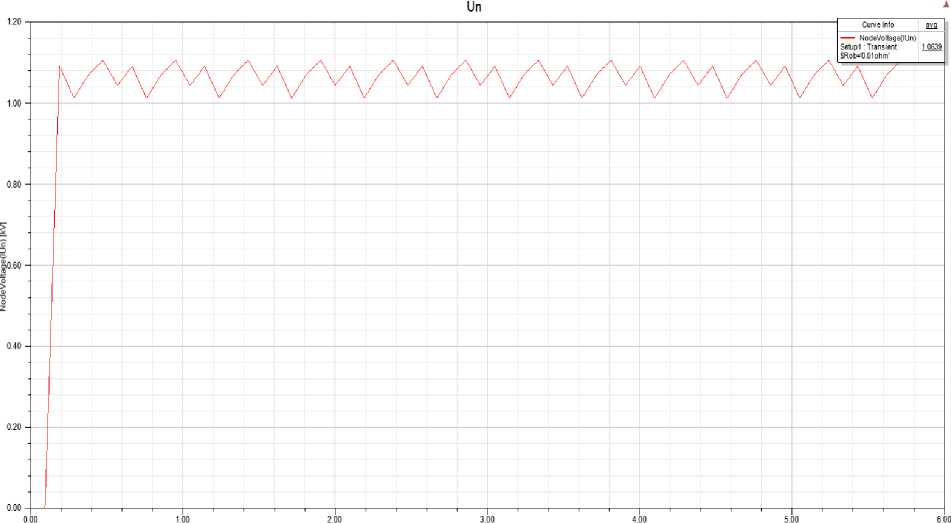
Производитель постоянных магнитов нормирует уменьшение параметра остаточной индукции Br на каждые 100 °С не более 15 %. Таким образом, имея поверочный тепловой расчет, можно рассчитать лишь минимально возможное напряжение [13]. При этом точно оценить уменьшение потока возможно лишь эмпирическим путем, так как второй предел уменьшения потока производитель не ограничивает. С использованием данных теплового расчета было проведено моделирование работы генератора на холостом ходу с нагретыми магнитами [14]. Осциллограмма напряжения изображена на рис. 4. Было получено значение 1064 В.

Далее в пакете ANSYS Maxwell был проверен номинальный режим работы генератора. Осциллограммы напряжения и тока представлены на рис. 5 и 6 соответственно.

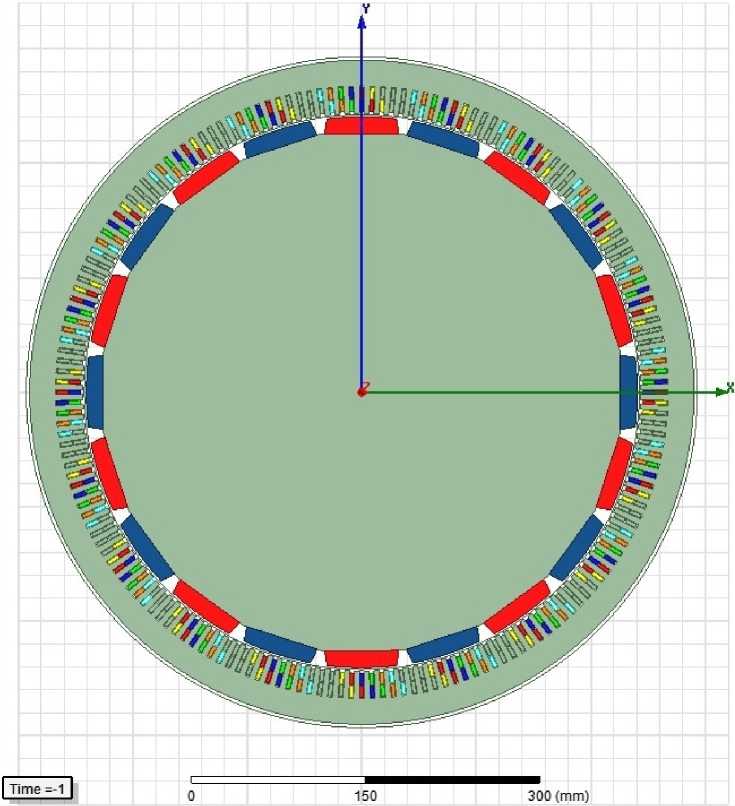
Рис. 1. Двухмерная модель проектируемого генератора в программе ANSYS Maxwell

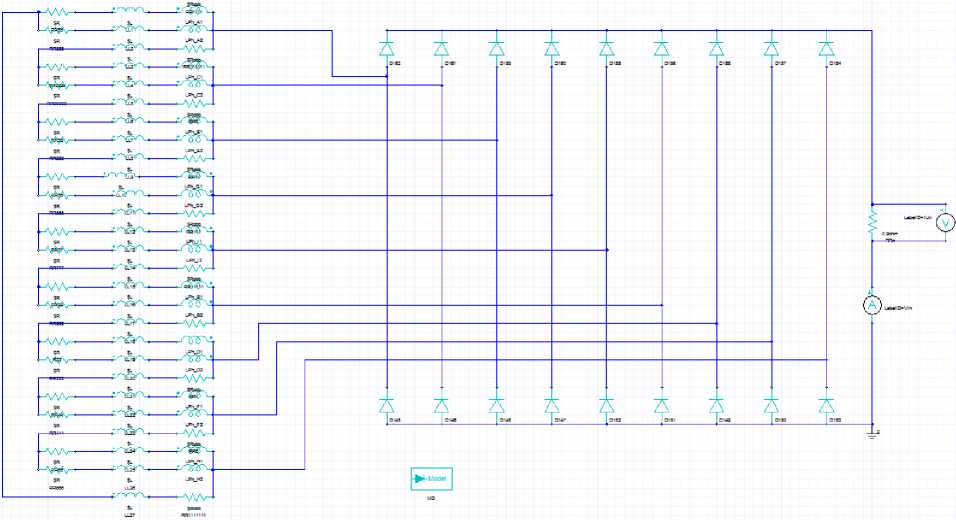
Рис. 2. Схема соединения обмотки генератора и подключения выпрямителя к нагрузке

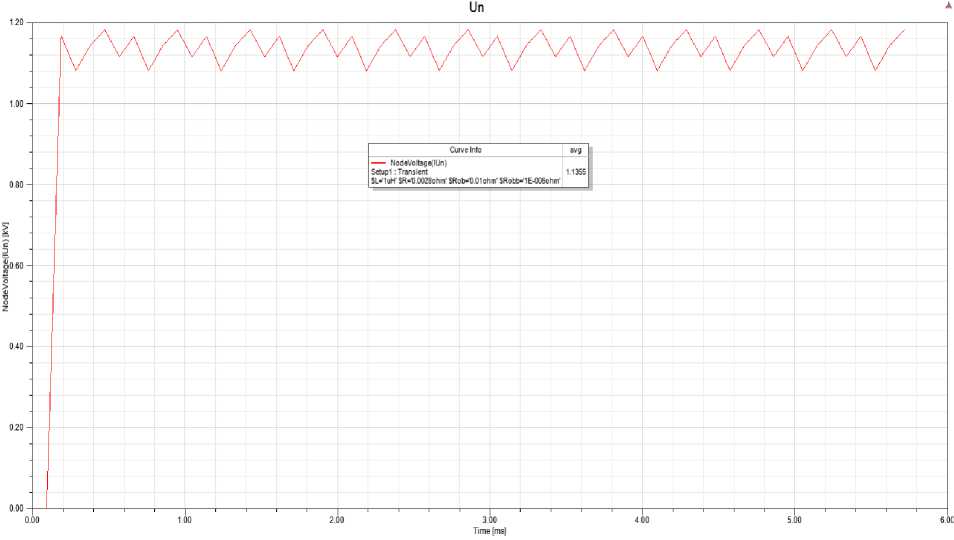
Рис. 3. Осциллограмма напряжения холостого хода при холодных магнитах

Time [ms]

Рис. 4. Осциллограмма напряжения холостого хода при нагретых магнитах

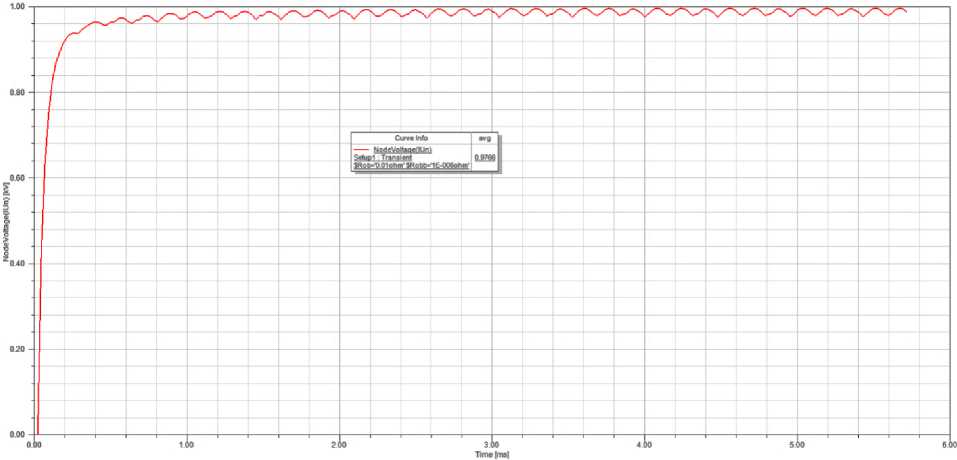
Рис. 5. Осциллограмма напряжения на выходе выпрямителя под нагрузкой (полученное значение 980 В)

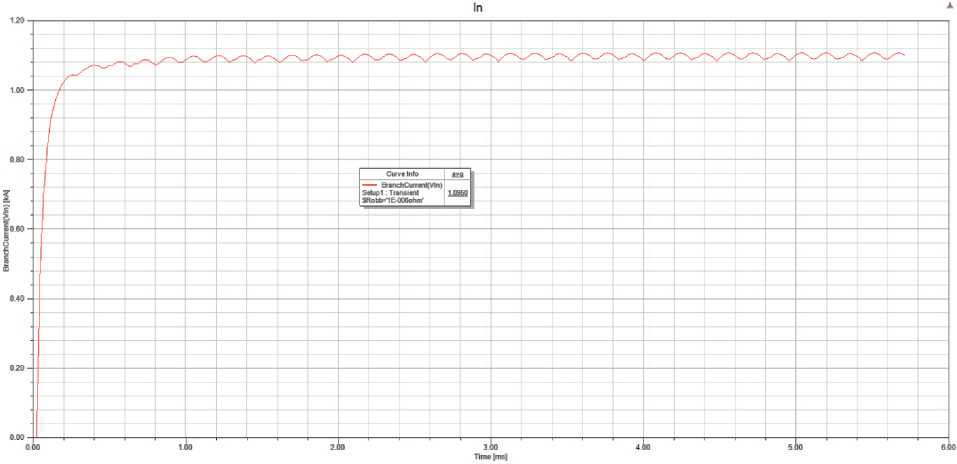
Рис. 6. Осциллограмма тока на выходе выпрямителя при номинальной нагрузке (полученное значение составляет 1100 А)

Также была проведена количественная оценка влияния эффекта вытеснения тока в пазу [15]. В паз генератора был заложен провод, представляющий из себя цельную медную шину. Под нагрузкой неизбежно возникает эффект вытеснения тока. Для стандартных асинхронных двигателей выбранные соотношения сторон провода и паза являются абсолютно приемлемыми, так как в стандартных асинхронных двигателях частота тока 50 Гц. В полученном генераторе частота тока в фазах составляет 350 Гц, вследствие чего эффект вытеснения тока в пазу усиливается, что приводит к резкому возрастанию потерь [16].

Количественная оценка влияния эффекта вытеснения тока по стандартным методикам

Вначале рекомендуется вычислить условную глубину проникновения тока в стержне, при этом принимается, что ток на данной глубине распределен равномерно.

Условная глубина проникновения тока:

a hr =

1 + Ф где a – высота провода в пазу, мм;

Ф - коэффициент, определяемый по эмпирическому графику в зависимости от безразмерного коэффициента ξ, называемого «численной» высотой стержня.

Определим ко эффициент :

^ = 2 п а - 10 - 1 -f - 10 " ⁵ = 2 л- 0,01 - 10 ^{- 1} х

\ bn Р

0,003    350

х                         - 10

\ 0,00410,01810 - 6

”⁵ = 2,37.

По эмпирическому графику определим коэффициент: ф = 1,4.

Отсюда определим условную глубину проникновения тока:

h = -ML = 4,167 - 10 — ³ , м.

r 1 + 1,4

Следующим шагом будет расчет сопротивления стержня с учетом вытеснения тока [17]. Известно, что от сопротивления потери в обмотке зависят прямо пропорционально:

Р эл = 1 2 R .                                    (6)

Следовательно, коэффициент увеличения сопротивления вследствие вытеснения тока будет равен коэффициенту увеличения потерь по указанной причине. Коэффициент увеличения сопротивления стержня определяется по формуле:

K r = 1 + ¹ 2^п Ф ,                              (7)

l ₂

где l ₂ – длина стержня;

• l _2п – длина пазовой части стержня без длины

в радиальных каналах.

Так как в исследуемом случае радиальные каналы отсутствуют, то описанные длины равны, а как следствие, их отношение равно 1.

Рассчитаем коэффициент увеличения сопротивления:

K r = 1 + 1 - 1,4 = 2,4.

Таким образом, согласно расчетам по эмпирическим формулам получено, что электрические потери вследствие вытеснения тока должны увеличиться в 2,4 раза. Точка максимального КПД должна сместиться в область значений ниже номинальной нагрузки, ориентировочно 650 кВт. Максимальный КПД изменится по значению и составит 95,5 % [18, 19].

Моделирование эффекта вытеснения токав ПО ANSYS Maxwell

Далее был проведен расчет в ANSYS Maxwell с учетом вытеснения тока в пазу.

На рис. 7 изображена картина пазового рассеяния машины. Видно, что существенная часть потока замыкается по пути рассеяния и не сцепляется с основным потоком [20]. Эти потоки рассеяния наводят ЭДС, различную по высоте шины, что приводит к возникновению различных по высоте шины плотностей тока.

На рис. 8 показано распределение плотностей тока в пазу электрической машины вследствие эффекта вытеснения тока. Таким образом, получаем нерациональное использование меди в пазу, часть провода не работает, а другая часть сильно перегружена.

Далее была получена осциллограмма суммарных потерь в шинах обмотки, называемых в ПО ANSYS Maxwell «SolidLoss». Осциллограмма потерь представлена на рис. 9. На рисунке можно увидеть, что суммарные потери в меди составляют 45 кВт, как и было получено во время испытаний машины.

Рис. 7. Картина магнитного потока машины

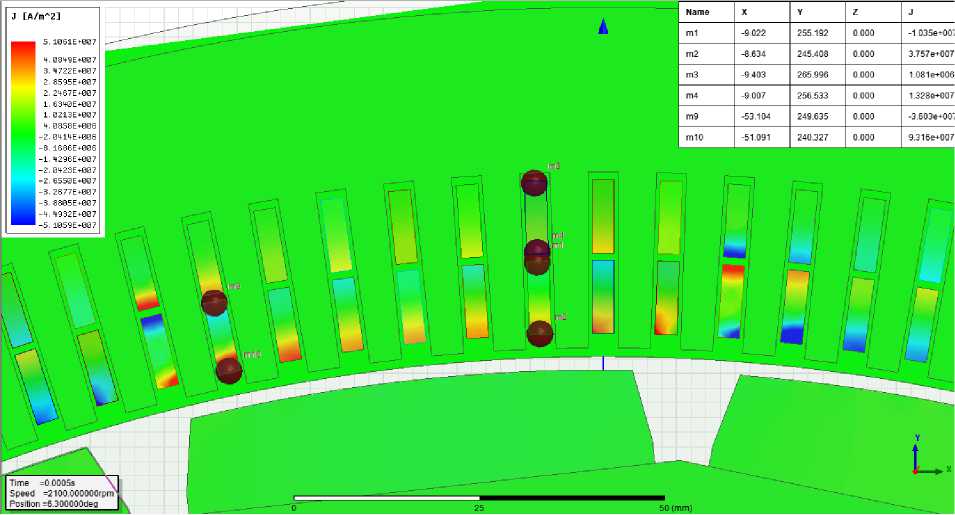
Рис. 8. Картина вытеснения тока в пазу

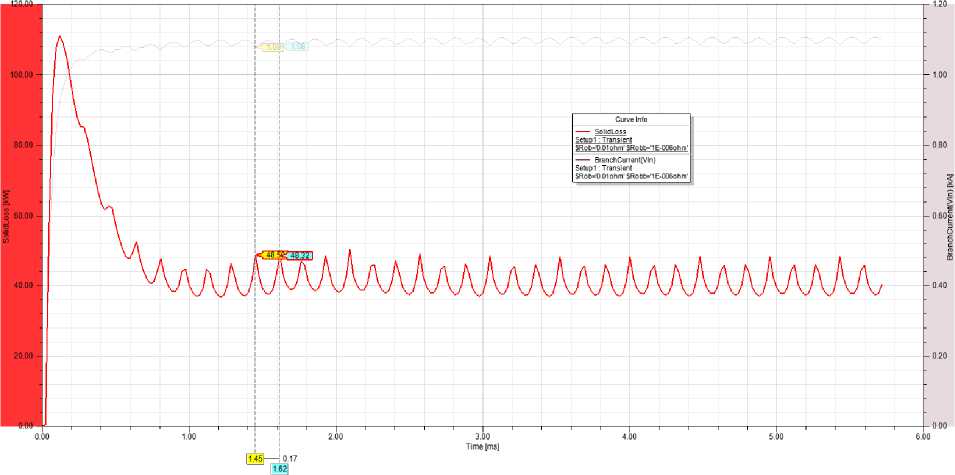
Рис. 9. Осциллограмма суммарных потерь в шинах обмотки генератора

Исходя из расчетов, проведенных в ANSYS Maxwell, следует вывод о том, что точка максимального КПД сместится в область более низких, относительного номинальной, нагрузок, ориентировочно 580 кВт. И величина максимального КПД в этом случае составит 95,1 %.

Заключение

На основании результатов проектирования генератора на АО «НПО «Электромашина» было изготовлено два макетных образца с использованием шин в пазах (с целью проведения научного экспе- римента) и с использованием расщепленной обмотки. Макетные образцы были испытаны. Полученные результаты испытаний макетного образца с шинной обмоткой показали: магнитные потери (определяемые на холостом ходу) соответствуют расчетным, электрические потери в обмотке при номинальной нагрузке соответствуют значениям, полученным при расчете в ANSYS Maxwell, и, как следствие, превышают величину, полученную по стандартным методикам. Максимальный КПД находился в области 580 кВт, что дополнительно подтверждает верность расчетов в ПО ANSYS Maxwell.

Также были проведены испытания второго макетного образца с расщепленной обмоткой. По результатам испытаний было подтверждено исключение влияния эффекта вытеснения тока при использовании в пазу расщепленной обмотки. Максимальный КПД, согласно опытным данным, составил 97,4 % и был получен в номинальной точке.

Таким образом, можно сделать вывод о том, что применение системы автоматического проектирования ANSYS Maxwell при расчетах количественного влияния эффекта вытеснения тока в обмотке машин переменного тока дает заведомо более точный результат, нежели ориентировочная оценка по стандартным методикам. Продемонстрирована легкость интерпретации всех результатов, получаемых при проектировании в ANSYS Maxwell, ввиду наглядности графического предоставления информации.

Также было показано, что электромагнитные расчеты в программном обеспечении ANSYS Maxwell аналогично подтверждаются при проведении испытаний изготовленных образцов в части всех характеристик, получаемых в процессе моделирования работы электромеханического преобразователя.