Применение систолических ортогональных преобразований в полиномиальной системе классов вычетов для повышения эффективности цифровой обработки сигналов
Автор: Калмыков Игорь Анатольевич, Зиновьев Анатолий Владимирович, Резеньков Денис Николаевич, Гахов Владислав Романович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 3 т.8, 2010 года.
Бесплатный доступ
Рассмотрена систолическая модель, реализующая ортогональные преобразования сигналов в расширенных полях Галуа GF(pv) на основе полиномиальной системы классов вычетов. Доказана возможность построения отказоустойчивых непозиционных спецпроцессоров ЦОС, способных сохранять работоспособное состояние за счет реконфигурации структуры при возникновении отказов.
Цифровая обработка сигналов, полиномиальная система классов вычетов, систолические ортогональные преобразования, отказоустойчивая система, реконфигурация структуры
Короткий адрес: https://sciup.org/140191413
IDR: 140191413 | УДК: 68
Текст обзорной статьи Применение систолических ортогональных преобразований в полиномиальной системе классов вычетов для повышения эффективности цифровой обработки сигналов
Известно, что использование методов цифровой обработки сигналов (ЦОС) позволяет относительно легко обеспечить высокую помехоустойчивость систем обработки данных, требуемую точность и разрешающую способность и ряд других преимуществ. Однако задачи ЦОС характеризуются выполнением больших объемов вычислений над большими массивами данных в реальном масштабе времени. Возрастание требований к технико-экономическим характеристикам современных систем ЦОС, расширение областей их применения и усиливающаяся тенденция к параллельным методам их организации привели к необходимости разработки и применения новых математических моделей ЦОС, базирующихся на модульной арифметике и обладающих свойствами кольца и поля. Реализация ортогональных преобразований в полиномиальной системе классов вычетов (ПСКВ) не только обеспечит реальный масштаб времени и высокую точность вычислений, но и позволит повысить отказоустойчивость вычислительного устройства ЦОС.
Постановка задачи
Существенное развитие телекоммуникационных технологий, наблюдаемое в последние годы, предоставление пользователям новых услуг требуют разработки и применения сетей с высокой пропускной способностью,обеспе- чивающих передачу мультимедийных данных в реальном масштабе времени.
Повысить эффективность таких технологий можно за счет широкого применения методов и алгоритмов цифровой обработки сигналов. Следует отметить,что такие технологические решения требуют обработки больших объемов данных в реальном масштабе времени.
Для решения задач, связанных с предоставлением таких услуг, как видео- и речевая связь, системы видеоконференций, голосовая почта, как правило, используются ортогональные преобразования в поле комплексных чисел,то есть на основе дискретного преобразования Фурье (ДПФ) или его быстрых алгоритмов (БПФ).
В качестве недостатков отмеченных моделей ЦОС можно выделить следующее [1-4]:
-
- поворачивающие коэффициенты являются иррациональными числами,что снижает точность вычислений;
-
- относительно низкая надежность функционирования спецпроцессоров (СП) цифровой обработки сигналов из-за наличия двух вычислительных трактов (для обработки действительных и мнимых частей).
Данных недостатков лишена модель ЦОС, обладающая свойствами кольца и поля. Такая модель реализуется в полях Галуа. При этом, используя гомоморфизм, порожденный китайской теоремой об остатках (КТО), можно организовать многомерную обработку сигналов с использованием полиномиальной системы классов вычетов, что позволит повысить скорость выполнения ортогональных преобразований сигналов [2; 4-5; 9]. Это обусловлено тем, что вычисления организуются в кольце полиномов P(z), представляющем собой сумму локального кольца полиномов Pl (z), образованного неприводимым полиномом pl (z) над полем GF(p), где l = 1; 2 … n ; n – количество локальных колец. Тогда вычисления N спектральных составляющих на основе обобщенного ДПФ в кольце полиномов определяется
X^z) = ^xnz)Pr(z)modPl(z) m=0
-
< N] , (I)
X^ (z) = ^x" (z)P^m(z)modpn (z) m=0
где {aM^X’^Je^z); к = 0; 1
N – 1. Характерной чертой системы уравнений является то,что для реализации обобщенного ДПФ в кольце полиномов используются операции сложения и умножения по модулю, которые довольно успешно реализуются в полиномиальной системе классов вычетов.В этом случае
|A(z)®B(z)|;(z)=|ai(z)®pi(z)|;(z), (2)
где ® – операции сложения,вычитания и умножения в GF(p);A(z) = и B(z) = – модулярный код в кольце полиномов;
a/z) = A(z)modpl(z);
p,(z) = B(z)modp,(z); 1= 1 ...n.
Другими словами, вычисления в ПСКВ организуются параллельно, помодульно и независимо друг от друга. При этом операции сложения, вычитания и умножения сводятся к соответствующим операциям над остатками по модулям pl(z) над полем.
Проведенные исследования показали, что применение математической модели ЦОС, реализованной в кольце полиномов третьей степени, позволило повысить скорость обработки данных на 8,3% по сравнению с реализацией теоретико-числового преобразования в кольце полинома шестой степени. Для дальнейшего повышения скорости обработки информации целесообразно использовать параллельно-конвейерные методы вычислений. Особое место среди таких методов обработки занимают систолические методы. Эти методы ориентированы на параллельно-конвейерное выполнение наиболее трудоемких вычислительных операций и позволяют эффективным образом реализовать широкий класс алгоритмов ЦОС путем обеспечения предельной для данного уровня технологии производительности вычислительных средств [5-6].
Параллельно-конвейерные вычислительные структуры систолического типа представляют собой множество однотипных, с точки зрения функциональных возможностей, процессорных элементов, называемых вычислительными ячейками (ВЯ). Все процессорные элементысо-единены между собой посредством локальных связей. При этом каждая ВЯ соединена только с ближайшими соседними вычислительными ячейками для передачи данных.
Основным принципом систолической системы является то, что все данные, регулярно и ритмически проходящие через массив ВЯ, используются многократно. Это позволяет значительно повысить эффективность СП ЦОС и достичь высокой вычислительной производительности за счет распараллеливания вычислений, сокращения времени обмена данными и совмещения процедур ввода, вывода и получения промежуточных результатов [6].
Следует отметить, что систолический принцип вычисления наиболее удачно реализуется в полиномиальной системе классов вычетов. Параллельная обработка информации по основаниям ПСКВ, независимость вычислений являются идеальной основой для применения параллельно-конвейерных вычислений в структуре модулярных СП ЦОС. В [5] приведены примеры построения непозиционных систолических спецпроцессоров первичной обработки сигналов, функционирующих в полиномиальной системе классов вычетов.
Следует отметить, что совмещение высокой производительности нетрадиционной полино-миальнойарифметикиипараллельно-конвейер-ной систолической организации вычислений позволяет осуществлять обработку сигналов в реальном масштабе времени для наиболее перспективных инфокоммуникационных технологий. Среди последних особое место занимает цифровая обработка изображения.
Известно, что цифровая обработка изображения требует выполнения двумерного ортогонального преобразования большого массива данных. Кроме того, цифровая обработка изображения характеризуется значительными вычислительными затратами. Так, согласно [10], обработка и анализ двумерного изображения размером 500×500 точек при использовании окна размерностью 30×30 пикселей требует порядка 200 млн. операций для проведения одного цикла расчетов.
Решить проблему, связанную с обеспечением реального масштаба времени обработки, можно за счет применения обобщенного ДПФ в кольце полиномов с использованием систолического принципа вычислений. Как прави- ло, двумерное ДПФ сводится к выполнению одномерных ДПФ с использованием процедур быстрого преобразования по каждой координате. В этом случае сначала N раз выполняется одномерное БПФ по строкам (столбцам), после чего N раз осуществляется вычисление аналогичной процедуры по столбцам (строкам) преобразуемого массива исходных данных. Однако строчно-столбцовый алгоритм цифровой обработки изображения характеризуется значительными временными затратами. Кроме того, такая реализация двумерного ДПФ предопределяет наличие дополнительной процедуры транспонирования матрицы промежуточных результатов, что также снижает скорость первичной обработки сигнала.
Применение систолического принципа вычислений позволяет обеспечить соответствие структуры многомерных данных линейной структуре вычислительного устройства ЦОС. Представив исходные данные в виде матрицы ХN размером N×N, запишем двумерное обобщенное ДПФ в кольце полиномов следующим образом:
CN mod^Cz^^E^^mod/^z);
-
< CN mod^Cz) = ((^E^^)mod^2(z);
CN mOd Pn (Z) = ((^ N EN }EN )mOd Pn (Z) '
где Xn =XN modpj(z); E^ =EN modp^z); EN – матрица поворачивающих коэффициентов, образующих мультипликативную группу ненулевых элементов порядка N.
Из выражения (3) следует возможность использования следующей параллельно-конвейерной процедуры двумерного обобщенного преобразование Фурье в кольце полиномов
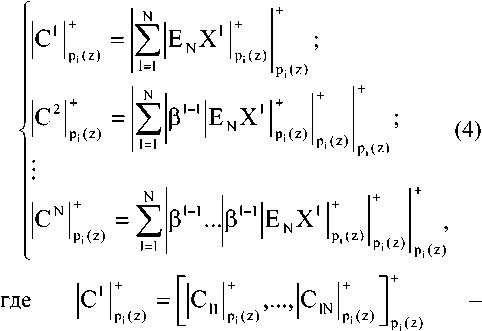
транспонированное представление вектора ко- нечных результатов ДПФ по модулю pi(z);
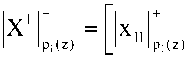
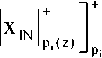
– транс-
понированное представление построчного вектора входных данных по модулю pi(z).
Основным достоинством рассмотренной процедуры вычисления обобщенного двумерного ДПФ в кольце полиномов является отсутствие в явной форме операции транс- понирования матрицы промежуточных результатов, что позволяет в значительной степени повысить быстродействие процессора ЦОС. Кроме того, при реализации цифровой обработки изображения целесообразно использовать систолические принципы вычисления.
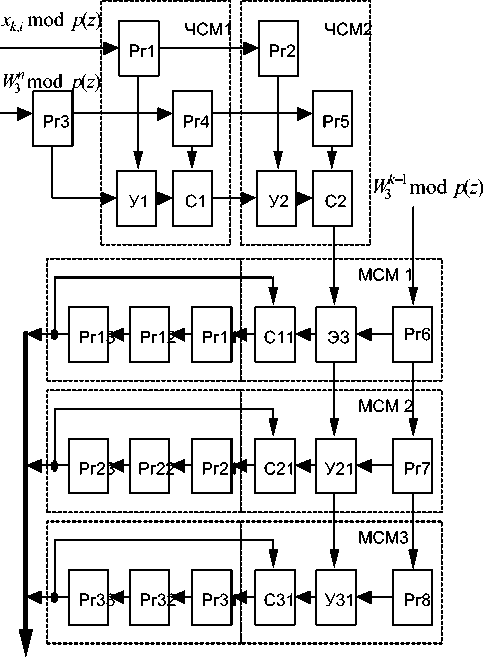
Преобразования вида lE"x'U соответствующие выполнению одномерного ДПФ по строке матрицы исходных данных, осуществляются на первой систолической матрице. Данная матрица является чистосистолической матрицей (ЧСМ) и содержит N – 1 вычислительную ячейку, имеющую одинаковую структуру. Каждая ячейка ЧСМ содержит два регистра для хранения, соответственно, значений входных отсчетов xy mod Pj (z) и поворачивающих коэффициентов W3n mod p, (z) = plj mod pj (z), взятых по модулю pi(z). Кроме того, в состав вычислительной ячейки входят модульный умножитель (Уj) и модульный сумматор (Сj), j = 1; 2 … N – 1. Дополнительные вычисления, соответствующие выполнению преобразований Фурье по второй коорди-нате,выполняются с помощью второй систолической матрицы. Данная матрица относится к многоканальным систолическим матрицам (МСМ) с блоком сдвиговых регистров (БСР). Матрица МСМ содержит N вычислительных ячеек, имеющих однотипную структуру.Каждая ячейка МСМ содержит регистр Рг для хранения значений коэффициентов W3k 1 modPj (z) = p(k ”j modPj (z), взятых по модулю pi(z). Кроме того, в состав вычислительной ячейки входят модульный умножитель (Уj) и модульный сумматор (Сj), j = 1 ; 2 … N. На рис. 1 представлена структура систолического процессора для вычисления двумерного ДПФ по модулю p(z) = z2 + z + 1.
Выход
Рис. 1. Структура систолического процессора для вычисления двумерного ДПФ по модулю p(z) = z2 + z + 1
Для данного полинома количество обрабатываемых данных при вычислении одномерного обобщенного ДПФ равно N = 3. Соответственно, такая матрица содержит две вычислительные ячейки ЧСМ1 и ЧСМ2, предназначенные для вычисления ДПФ по первой координате, а также три вычислительные ячейки МСМ1, МСМ2 и МСМ3, используемые для выполнения полиномиального преобразования Фурье по второй координате. Так как данное преобразование имеет размерность 3×3, то каждый из трех БСР содержит по три регистра Ргj1, Ргj2, и Ргj3, j = 1; 2; 3, предназначенных для хранения промежуточных и окончательных результатов вычисления двумерного обобщенного ДПФ. При этом регистры в БСР соединены таким образом, что организуют кольцевую передачу в канал от соответствующей вычислительной ячейки МСМ данных от входа к выходу и с выхода на вход соответствующего модульного сумматора Сj.
Управление ходом вычислений в процессоре осуществляется счетчиком числа строк (счетчик k), определяющим номер вводимой в процессор строки данных и весового множи- теля, поступающего на вход матрицы МСМ1 , а также счетчиком числа элементов строки или числа столбцов матрицы (счетчик n), определяющим весовые множители, поступающие на вход матрицы ЧСМ1.
Оценим время выполнения двумерного преобразования Фурье матрицы данных размером N×N отсчетов в систолическом процессоре, структура которого представлена на рис. 1. Если время выполнения базовой операции в ВЯ составляет один такт, то на выходе первой матрицы типа ЧСМ первый коэффициент одномерного ДПФ по строке матрицы данных, представленный в виде остатка по модулю pi(z), будет сформирован через N – 1 тактов. При этом ВЯ включаются в параллельную работу со второго такта. Последний коэффициент одномерного ДПФ по строке данных, представленный в ПСКВ, будет сформирован через 2(N – 1) тактов.
Загрузка элементов следующей строки данных в ВЯ матрицы MCМ начинается с (N + 1)-го такта и производится параллельно с формированием коэффициентов ДПФ по предыдущей строке данных. Завершится она через N тактов. Кроме того, N тактов требуется на загрузку элементов первой строки данных. С учетом этих факторов, а также холостых операций время выполнения одномерного ДПФ всей матрицы данных составит
T, = (2N2 +N-2)t, (5)
где т - длительность такта.
При этом длительность такта будет определяться временем выполнения операций модульного умножения и модульного сложения:
T = V+V (6)
Дополнительное время, требуемое на обработку матрицы по второй координате, составит
T2=Nt. (7)
Таким образом, полное время выполнения обобщенного двумерного ДПФ в кольце поли-номов,используя систолический принцип вычислений, будет равно
T = T, +T2 =2(n(N + 1)-1)t. (8)
Время считывания результатов из блока сдвиговых регистров равняется Тсч =N2tC4.
Кроме указанных матриц ЧСМ и МСМ с блоком сдвиговых регистров в состав спецпроцессора, функционирующего в кольце полиномов, входят преобразователь из позиционного кода в код ПСКВ и преобразователь, осуществляющий обратную процедуру – перевод модулярного полиномиального кода к позиционному виду. Следует отметить, что выбор алгоритмов, необходимых для выполнения этих немодульных операций, оказывает существенное влияние как на аппаратурные, так и на временные характеристики непозиционного спецпроцессора. В работе [1] представлены результаты анализа основных методов и алгоритмов прямого и обратного преобразований. Полученные результаты позволяют обоснованно выбрать метод непосредственного суммирования для реализации прямого преобразования из двоичного кода в код ПСКВ, а для выполнения обратного преобразования – метод, базирующийся на китайской теореме об остатках с использованием ортогональных базисов. Следует отметить, что схемные реализации этих методов характеризуются минимальными временными и аппаратурными затратами по сравнению с другими методами выполнения этих немодульных операций [2].
Проведенные исследования показали, что совмещение достоинств модульного представления данных с систолической обработкой позволило повысить скорость вычисления двумерного ДПФ на 18,9% при использовании четырех модулей шестой степени по сравнению с реализацией цифровой обработки изображения на основе 24-разрядного СП БПФ. Полученные результаты свидетельствуют о целесообразности совместного использования ПСКВ и пространственно-временной организации вычислительного процесса для синтеза спецпроцессоров первичной обработки сигналов, функционирующих в реальном масштабе времени.
Следует отметить, что применение полиномиальной системы классов вычетов позволяет не только повысить скорость обработки данных, но и обеспечить требуемый уровень отказоустойчивости СП ЦОС [2; 8-9].
Если из множества n неприводимых полиномов, составляющих систему ПСКВ, выбрать только k, то есть определить рабочий диапазон
к
Рраб(2) = ПР|(2)’
то оставшиеся г (r = n-k) модулей могут быть использованы для выполнения процедур поиска и коррекции ошибок.
Многочлен A(z) с коэффициентами из поля будет считаться разрешенным в том и только в том случае, если A(Z)GPpa6(Z). Тогда местоположение A(z) относительно Рраб (z) позволяет однозначно определить, содержит ли код ПСКВ ошибочные символы.
В [2] проведены исследования корректирующих способностей кодов ПСКВ. Проведенные исследования позволили определить минимальную избыточность, необходимую для обнаружения и коррекции ошибок заданной кратности.
Для поиска и исправления ошибок в кодах полиномиальной системы классов вычетов используются различные позиционные характеристики. Поскольку в результате ошибки полином A(z) = (a, (z),...,ak(z),ak+1(z),ak+2(z)) превращается в ошибочный полином A*(z), лежащий вне рабочего диапазона, то, зная номер интервала, куда попал искаженный полином A * (z), можно однозначно определить отказавшее основание,а также величину ошибки. Следовательно, для процедур поиска и коррекции ошибок можно воспользоваться интервальным номером.
Процесс определения данной характеристики осуществляется согласно выражению lHHT(z) = [A(z)/Ppa6(z)]. (10)
Несмотря на то, что процедура (12) относится к немодульным, ее сводят к совокупности модульных операций. В [2] представлено устройство, осуществляющее обнаружение и коррекцию ошибки в модулярном полиномиальном коде на основе вычисления интервального номера. Так как множество значений интервального номера lинт(z) представляет собой кольцо по модулю Pконт(z), выражение (10) преобразуется к виду
1„ht(Z) =
^a^R^ + K*^) , (ii)
1=1 A,„iz)
k+r где Rj(z) = [Bj(z)/Ppa6(z)]; РК0нт = ПрА2);
ранг безызбыточной системы определяется как
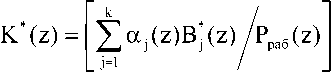
Для обеспечения меньших временных затрат на процедуры вычисления интервального номера полинома целесообразно использовать изоморфизм, порожденный китайской теоремой об остатках. В этом случае равенство имеет вид
1™'(Z) = Z|ai(z)B*(z)| ;(z) + £ai(z)Ri(z)
i=k+l e^t^E*^
k+r
+ E+^M2) i=k+l
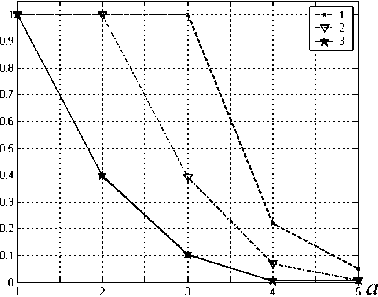
Pk+r Проведенные исследования показали, что реализация процесса вычисления интервального номера согласно (13) позволила обеспечить наибольшую эффективность при контроле и исправлении ошибок, возникающих в процессе функционирования спецпроцессора ЦОС. При этом представленный алгоритм вычисления данной позиционной характеристики отличается довольно высокой надежностью работы при сравнительно небольших временных затратах на реализацию процедур поиска и определения местоположения ошибочных разрядов. Рассматривая вопросы построения отказоустойчивых непозиционных СП цифровой обработки сигналов, следует отметить, что полиномиальная система классов вычетов позволяет не только обнаруживать и исправлять ошибки, но и обеспечивать работоспособное состояние спецпроцессора первичной обработки сигнала при возникновении последовательности отказов за счет снижения в допустимых пределах основных показателей качества функционирования. Известно, что одним из наиболее эффективных методов борьбы с последовательностью отказов, возникающих в процессе функционирования СП ПСКВ, является реконфигурация структуры устройства. Применение данного метода позволяет сохранить работоспособное со-стояниеспецпроцессорузасчетперераспределе-ния вычислительной нагрузки. В основу метода реконфигурации положены обменные операции ПСКВ. Изменяя количество информационных и избыточных оснований, можно варьировать точность, скорость и достоверность обработки данных. Метод реконфигурации сводится к выполнению следующих операций [2]: - определение отказавшего основания полиномиальной системы класса вычетов; - отключение отказавшего основания; - перераспределение оставшихся работоспособных вычислительных трактов между множеством информационных и избыточных оснований деградирующего СП. Для эффективной реализации метода реконфигурации СП ПСКВ были проведены исследования распределения ошибочных интервалов при постепенной деградации структуры вычислительного устройства. Полученные результаты показали, что существуетвозможность определения интервального номера ошибочного полинома при любом сочетании в ансамбле оснований ПСКВ. Однако это не позволило в полной мере воспользоваться достоинствами модулярного полиномиального кода при разработке метода реконфигурации. Основным сдерживающим фактором широкого применения обменных операций при построении живучих спецпроцессоров, функционирующих в ПСКВ, является отсутствие алгоритмов пересчета ортогональных базисов при постепенной деградации структуры вычислительного устройства. Это не позволяет обеспечить высокоэффективное обратное преобразование из модулярного полиномиального кода в позиционный двоичный код. Решить данную проблему можно за счет применения данной теоремы, которую можно положить в основу алгоритма вычисления новых значений ортогональных базисов при отказе модулей ПСКВ. Теорема. В избыточной ПСКВ с основаниями p1 (z), p2(z) … pk+r(z) при деградации по j-му модулю значение ортогональных базисов новой системы оснований будет определяться B-(z) = mod р; (z^ P[ (z) ■ (14) 1=1 Доказательство. Согласно китайской теореме об остатках значение ортогонального базиса определяется из условия В; (z) = Imodpj (z), (15) где i = 1; 2 ... к + r. Тогда его значение будет задаваться следующим выражением: Bi(z) = mi(z)P(z)/pi(z), (16) где mi(z) – вес i-го ортогонального базиса; k+r p(z) = IIPi(z) ПСКВ. – полный диапазон оснований Упростив последнее равенство, получаем k+r Bi(z)-m,(z)]_[pl(z) 1=1 Известно, что значение веса ортогонального базиса определяется из условия т;(г)5;(г) = Imodpj(z) , (18) при величине второго сомножителя в выражении (18), задаваемой выражением Подставляем последнее равенство в выражение (21) и при этом учитываем условие (20). Тогда получаем следующее значение ортогонального базиса в деградирующей ПСКВ: k+r k. l*ij k+r )ПР|(2)- 1=1 l*i.J 5i (z) = modp/z) Пусть в системе оснований ПСКВ произошла деградация по j-му основанию. Тогда новая система содержит следующие модули: p1 (z), p2(z) … pj-1(z), pj+1(z) … pk+r(z). При этом полный диапазон новой деградирующей системы ПСКВ будет определяться согласно равенству Следовательно, используя выражение (16), можно вычислить новые значения ортогональных базисов Теорема доказана. Данная теорема может стать основой для разработки алгоритма реконфигурации структуры спецпроцессора ПСКВ,применение которого позволит сохранить работоспособное состояние СП ЦОС за счет снижения в допустимых пределах основных показателей качества функционирования. Для оценки эффективности разработанного алгоритма реконфигурации был проведен сравнительный анализ СП ПСКВ, реализующего этот алгоритм, с процессором, использующим корректирующие способности кодов ПСКВ, а также с позиционным процессором, имеющим троированную мажоритарную структуру. Результаты исследования приведены на рис. 2. В качестве целевой функции был выбран показатель коэффициента запаса работоспособности, определяемый как B/z) = m:'(z)PJ(z)/p1(z), (21) где i=l;2...j-l,j + l ... к + r. Тогда значение веса ортогонального базиса в деградирующей системе оснований ПСКВ будет определяться как a a / a ’ (25) где На – число работоспособных состояний спецпроцессора при возникновении а = 1; 2 … отказов элементов в подсистемах устройства; Na – общее число возможных состояний спецпроцессора при отказах а = 1; 2 … элементов. m;'(z)5/z) = 1 modp/z). (22) При этом величина второго сомножителя в последнем равенстве задается выражением 5/z) modp/z). Разделив обе части (22) на равенство (23), получаем Рис. 2. Изменение коэффициента запаса работоспособности СП при накоплении отказов элементов а = 1; 2… (кривая 1 – с реконфигурируемой структурой; 2 – с коррекцией ошибки; 3 – с реализацией метода «2 из 3») m/z) = Анализ графика показывает,что применение корректирующих кодов ПСКВ позволяет повысить отказоустойчивость процессоров класса вычетов по сравнению с классическим методом маскирования отказов «2 из 3». Использование трех контрольных оснований позволяет однозначно исправлять все двукратные ошибки, возникающие в процессе функционирования процессоров ПСКВ. При возникновении третьей ошибки запас работоспособности такого вычислительного устройства уменьшается до значения Зп = 0,390. Применение разработанного алгоритма реконфигурации структуры непозиционного процессора позволяет повысить отказоустойчивость системы. Реализация перераспределения ресурсов при возникновении отказов вычислительных трактов позволяет обеспечить работоспособное состояние процессора ПСКВ даже при накоплении трех отказов. При этом данный процессор осуществляет процедуру обработки данных с использованием трех рабочих и двух контрольных оснований. Следует отметить, что в этом случае вычислительное устройство способно обнаружить факт наличия многократной ошибки в процессе своего функционирования. Проведенные исследования показали, что схемные затраты, необходимые на реализацию вычислительной системы ЦОС, построенной на основе отказоустойчивого непозиционного процессора ПСКВ, составляют 79% от аппаратурных затрат на многопроцессорное позиционное устройство ЦОС, реализующего метод маскирования отказов «2 из 3». Применение полиномиальной системы классов вычетов позволяет повысить скорость обработки данных более чем в 1,18 раза даже по сравнению с быстрыми алгоритмами обработки сигналов в позиционной системе счисления. Обобщая сказанное выше, можно сделать вывод о том, что совмещение особенностей модулярного избыточного кодирования в ПСКВ с систолическими принципами организации ортогональных преобразований сигналов позволяет не только обеспечивать высокую скорость обработки данных, но и разрабатывать вычислительные устройства, обладающие свойствами устойчивости к последовательностям отказов и сбоев.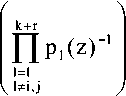
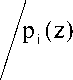
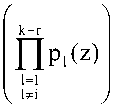
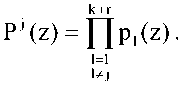
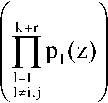
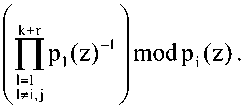
Список литературы Применение систолических ортогональных преобразований в полиномиальной системе классов вычетов для повышения эффективности цифровой обработки сигналов
- Червяков Н.И., Калмыков И.А., Галкина B.А. и др. Элементы компьютерной математики и нейроноинформатики. Под ред.Н.И. Червякова. М.: Физматлит, 2003. -216 с.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов. Под ред. Н.И. Червякова. М: Физматлит, 2005. -276 с.
- Вариченко Л.В. Абстрактные алгебраические системы и цифровая обработка сигналов. Киев: Наукова думка, 1986. -247 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа//Нейрокомпьютеры: разработка и применение. № 6, 2003. -C. 61-68.
- Калмыков И.А., Зиновьев А.В., Емарлукова Я.В. Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем//ИКТ. Т.7, № 2, 2009. -С. 31-37.
- Кун С. Матричные процессоры на СБИС. Пер с англ. М.: Мир, 1991. -671 с.
- Калмыков И.А., Хайватов А.Б. Математическая модель отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов//ИКТ. Т.5, № 3, 2007. -С. 39-42.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О. и др. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов//Нейрокомпьютеры: разработка, применение. № 12, 2004. -С. 51-60.
- Калмыков И.А., Резеньков Р.Н., Тимошенко Л.И. Непозиционное кодирование информации в конечных полях для отказоустойчивых спецпроцессоров цифровой обработки сигналов//ИКТ. Т.5, № 3, 2007. -С. 36-39.
- Татузов А.Л. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов//Нейрокомпьютеры: разработка, применение. № 5-6, 2004. -С. 37-44.


