Применение скользящей шкалы приоритетов в задачах оптимизации управления

В современной практике управления в большинстве случаев решение задач оптимизации предполагает применение типовых или адаптированных алгоритмов линейного программирования [2]. Стандартные алгоритмы требуют довольно громоздкого математического аппарата и применения машинных методов, поэтому для реальных управленческих задач вводятся допущения с целью упростить модель, а значит, и процесс ее обработки. Однако изменения в глобальной экономике последних лет, связанные с нефинансовым санитарным кризисом и ростом политико-экономической напряженности и сопровождающими их финансовыми и сырьевыми кризисными состояниями, свидетельствуют о резком росте степени неопределенности. Данный фактор необходимо принимать во внимание в процессе принятия управленческих решений. Одним из возможных подходов является применение энтропийного моделирования [8; 12]. Однако необходимо понимать, что энтропийные модели, во-первых, не очень удобны для использования управленцами

Применение скользящей шкалы приоритетов в задачах оптимизации управления

Вечерская Светлана Евгеньевна кандидат химических наук, доцент, доцент кафедры информационных систем в экономике и управлении. Российский новый университет, Москва. Сфера научных интересов: эффективность управления; эконометрика. Автор более 40 опубликованных научных работ.

в повседневной практике, во-вторых, не позволяют выделить и задействовать те конкретные метрики управления, которые могут быть измерены и непосредственно в процессе производственной деятельности. В связи с этим заслуживает внимание другой подход, который можно обозначить как метод скользящей шкалы приоритетов.

История применения скользящей шкалы

Исторически понятие скользящей шкалы возникло и до сих пор находит широкое применение в сырьевом бизнесе, в частности нефтяном [5], а также при дифференциации мотивационных денежных механизмов, в том числе определении зарплатных контрактов и ценовых механизмов. Так, скользящая шкала определяется как соотношение показателя выручки от реализации продукции и фактора, на который должна быть скорректирована эта прибыль, причем корректирующий фактор определяется статистическими методами на основе закона равномерного распределения [11]. Системы со скользящими шкалами используются для того, чтобы при росте прибыльности производственных проектов росли бюджетные доходы. Большинство фискальных систем таковы, что их прибыльность напрямую зависит от доли государства. Как правило, для обеих сторон выгоднее, если доля государства является функцией прибыльности. Это определяется главной целью систем, ориентированных на внутреннюю доходность [1]. С учетом установленных зависимостей строится скользящая шкала ожидаемых доходов и налоговых поступлений в государственный бюджет [6].

Одним из примеров индексации является использование скользящей шкалы в договорах о заработной плате. Индексация контрактов, например, в соответствии с темпом инфляции, минимизирует инфляционную нагрузку и связанные с ней издержки. Распространенность применения скользящих шкал для определения величин заработной платы в ряде случаев зависит от особенностей национальных экономик [13]. Обработка алгоритмов скользящей шкалы обычно проводится с применением машинных методов [9].

Существует также понятие скользящего прогноза, который представляет собой тип финансовой модели, прогнозирующей будущие показатели бизнеса в течение непрерывного периода на основе исторических данных. В отличие от статических бюджетов, которые прогнозируют будущее на фиксированный период времени, скользящий прогноз регулярно обновляется [14]. Во всех рассмотренных примерах оптимизация управления не является целью и даже не всегда принята во внимание.

Метод и модель

Введение приоритетов в скользящую шкалу в общем случае должно способствовать повышению точности оптимизационной модели благодаря учету не столько вероятностных факторов, сколько именно фактора приоритета тех или иных параметров. В условиях роста неопределенности приоритеты становятся всё более значимыми как для стратеги- ческого, так и для операционного управления, давая возможность ограничить повышение сложности [3] модели управляемой системы.

Рассмотрим параметры, которые можно отнести к значимым с точки зрения приоритезации в управлении. Модели оптимизации управления включают две принципиально различающиеся группы измеряемых значений – параметры целевой функции (начальные и граничные) и собственно целевые функции. В зависимости от причин появления и/или роста неопределенности «скользить» будут те или иные параметры.

Сами причины появления неопределенности не будут существенным образом влиять на модель. Однако их природа также важна с точки зрения управления. Можно разделить эти причины на две большие группы. К первой группе относятся условно объективные внешние факторы, которые часто обозначаются как форсмажор; ко второй – субъективные факторы, связанные с особенностями управления рассматриваемой системой, – стиль управления, степень доминирования личностных факторов при принятии решений, стремление к автаркии или высокорисковым проектам и др. При этом нужно учесть, что некоторые ситуации, которые традиционно относятся к форсмажору (например, военные действия), являются субъективными по своей сути, и их надо рассматривать в рамках второй группы. В случае преобладания факторов первой группы основной целью управления становится сохранение, насколько это возможно, устойчивости системы. Часто это выглядит как выживание, и речь об оптимизации не идет.

Моделирование с последующей оптимизацией, напротив, будет вполне востребовано в случае действия субъективных факторов управления, меняющих соотношение параметров оптимизации. Как отмечено выше, возможны два типа ситуаций, когда скользящую шкалу необходимо ввести либо для параметров целевой функции, либо для самой целевой функции. В первом случае целевая функция будет иметь вид

F j< var> x . ) > { F j x . , x e x _rj, ... F j x i .„ x x ,x _v , x j},            (i)

где F _fix – фиксированная целевая функция; x _i – параметр целевой функции; < var>x _i – функция вероятностного изменения x _i , изменяющегося в диапазоне значений [ x _i , x _ω ]; число параметров, учитываемых в целевой функции, может быть различным.

Для изменяющегося приоритета целевой функции выражение изменится:

F ( x . ) >  < var>F ( x . ),                                 (2)

где varF ( x _i ) – изменяющаяся целевая функция.

Важно отметить, что вариативность относится именно к диапазонам значений параметров, а не значениям как таковым, которые, по определению, являются переменными зависимыми либо независимыми.

Для простейшего случая функции F ( x ) соответствующие зависимости показаны на двумерной плоскости (см. Рисунок 1). На одном и том же интервале переменной x ожидаемое значение целевой функции может уменьшаться или увеличиваться. На практике это будет означать возможность достижения заданного значения при значении x , отличном (меньше или больше в зависимости от постановки задачи) от x _opt (см. Рисунок 1, а ). Можно также зафиксировать значение целевой функции при изменяющихся диапазонах x (см. Рисунок 1, b ).

Примеры из практики управления

Проиллюстрируем предложенные варианты модели на примерах из управленческой практики. Прежде всего следует определиться с возможными причинами возникновения

Применение скользящей шкалы приоритетов в задачах оптимизации управления необходимости введения скользящей шкалы приоритетов. Существует довольно много задач оптимизации управления, при решении которых достаточно строить модель с фиксированными диапазонами параметров оптимизации и/или исходить из ожидаемых значений целевой функции в фиксированных пределах значений (определяемых показателями внутренней и внешней сред предприятия).

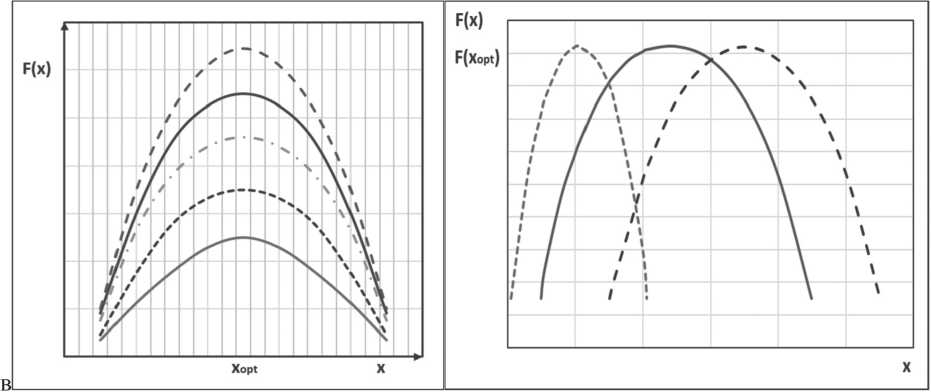
a                                       b

Рисунок 1. Скользящая шкала для целевой функции ( а ), для параметров целевой функции ( b )

В тех случаях, когда преобладает директивный, авторитарный стиль руководства, математическое ожидание значения целевой функции приобретает субъективный характер. Так, например, естественно было бы ожидать, что максимизация выручки предприятия или доходов бюджета является одним из разумных вариантов оптимизации. Однако если руководитель определит в качестве приоритетных такие направления, как ребрендинг, техническое перевооружение или географическая экспансия, которые существенно снижают доходность и даже могут привести к убыточности, будет наблюдаться смещение приоритетов и изменение диапазона возможных значений целевой функции. Сама по себе доходность при этом сохранит свою целевую значимость. На длинных горизонтах планирования можно предположить возвращение ожидаемых значений в исходный диапазон, однако лишь с определенной долей вероятности. На коротких горизонтах введение скользящей шкалы будет учитывать именно смену приоритетов.

Описанный в работе [4] пример изменения модели воронки продаж показывает, что, сохраняя задачу максимизации целевой функции прибыли, но меняя параметры организационной структуры, компания использует скользящую шкалу для целевой функции и при этом не только может обеспечить максимальную эффективность своей деятельности, но и оптимизировать организационную структуру.

Фиксированное ожидаемое значение целевой функции при изменениях параметров также часто обусловлено именно внутренними процессами принятия решений, но может быть и следствием макроэкономических изменений. Так, возможно изменение диапазонов такого параметра, как стоимость капитала (например, в силу оттока иностранного капитала с национального рынка или невозможности привлечения инвесторов). Комплексные модели с большим набором вариативных параметров обычно используются при управлении инвестиционными портфелями и паевыми фондами. Похожий эффект оказы- вает применение инновационных стандартов управления, например, стандарта ESG [7], который требует от предприятий определенных ограничений и инвестиций, хотя подобные стандарты нельзя считать строго необходимыми; это, скорее, своеобразные «запросы извне», следование которым приведет к смещению ожидания целевой функции и будет определяться во внутренних процессах принятия решений.

Обобщенная модель

Существенным является вопрос о том, как, собственно, обрабатывать модели, получаемые с учетом скользящих шкал приоритетов. Имеющиеся алгоритмы оптимизации хотя и являются непростыми и иногда даже громоздкими для применения их на практике, но введение дополнительных функций изменения параметров, очевидно, приведет к еще большему их усложнению. Тем не менее можно показать, что оптимизационные модели, учитывающие возрастание степени неопределенности вследствие появления скользящей шкалы, в большинстве случаев не выходят за рамки математического программирования. Так, на Рисунке 2 представлена матрица распределения методов оптимизации в зависимости от вариативности параметров.

F(x)

Стохастическое программирование	Энтропийное моделирование
Линейное программирование	Динамическое программирование

Фиксированная         Скользящая х шкала              шкала

Рисунок 2. Выбор математических методов оптимизации

Верхний правый квадрант отличается тем, что вариативность, соответственно, и степень неопределенности обоих типов параметров оказываются высокими, и зафиксировать какой-либо из них невозможно. Для многофакторных моделей такая ситуация граничит с хаосом, и для ее описания наилучшим образом подойдет именно вероятностная модель. Проблемой, однако, останется невысокая практическая применимость такой модели. Но в данном случае стоит напомнить, что в ситуации управленческого хаоса, как и в случае форсмажора, главной задачей управления становится сохранение устойчивости системы, а не ее оптимизация. Поэтому здесь будет оправдан энтропийный подход [10].

Применение скользящей шкалы приоритетов в задачах оптимизации управления

Заключение

Таким образом, процесс выбора модели оптимизируемой системы должен включать качественную оценку степени неопределенности (вариативности) всех параметров целевой функции. На основании этой оценки осуществляется выбор математического метода решения задачи оптимизации. Методы математического программирования могут быть использованы для большинства задач управления, причем скользящая шкала приоритетов для целевой функции приведет к необходимости применения стохастического программирования, а для скользящей шкалы параметров целевой функции достаточно будет варианта линейного программирования – динамического программирования.