Применение слепой обработки сигналов для подавления шумов спеклов в лазерной триангуляции

На производстве часто поднимается вопрос оценки геометрических параметров для решения задач технической диагностики и неразрушающего контроля. Наиболее часто данная проблема возникает на железнодорожном транспорте в системах измерения геометричес- ких параметров рельсов. Основным требованием, предъявляемым к подобным системам, является высокая точность и возможность работы с поверхностями любой сложности.

Одним из наиболее часто применяемых в последнее время методов бесконтактного измерения геометрического профиля объекта является метод лазерной триангуляции. Этот метод получил широкое распространение благодаря своей простоте, надежности и высокой точности. Принцип лазерной триангуляции изображен на рис. 1.

Когерентное излучение с выхода лазера попадает на вход развертывающей системы, представляющую собой в простейшем случае цилиндрическую линзу. На выходе системы развертки лазерный луч представляет собой линию (световое пятно S ), проецирующуюся на поверхность объекта. Отражаясь от поверхности объекта, лазерный луч проходит узкополосный оптический фильтр с системой фокусировки и попадает на CMOS матрицу. Изображение, формируемое на CMOS матрице, содержит информацию о профиле объекта. Ось излучения образует с осью наблюдения угол 0. Если переместить поверхность объекта на малую величину kz , то изображение на матрице сдвинется на величину kx.

Рис. 1. Принцип лазерной триангуляции

Исходя из геометрических соображений можно записать

Ах = Р • Az -sin#, (1)

где обозначения соответствуют рис. 1. Параметр P является коэффициентом усиления конкретной системы фокусировки, в дальнейших рассуждениях принимается равным единице. Следует особо подчеркнуть наличие узкополосного оптического фильтра, его применение носит двоякий характер. С одной стороны, он позволяет убрать большую часть помех, связанных с общим освещением, и тем самым повысить точность измерения, с другой стороны, его наличие требует применения когерентного источника света с узким спектром излучения. Именно применение когерентного излучения делает возможным появление шумов спеклов, которые вносят основной вклад в искажение изображения. Под спеклом (от английского слова speckle – крапинка, пятнышко) понимается случайная интерференционная картина, которая образуется при взаимной интерференции когерентных волн, имеющих случайные сдвиги фаз и/или случайный набор интенсивностей [4]. Помимо шума спеклов на изображение накладывается аддитивный шум (шум квантования АЦП матрицы, тепловые шумы и т.п.), а также шум, связанный с эффектом блюминга (blooming), вызванный растеканием заряда по CMOS матрице при ее насыщении.

Оценка минимально достижимой погрешности измерения положения триангуляционным методом

На рис. 2 представлено изображение, полученное сканированием круглого объекта диаметром 32 мм.

Для получения координат профиля объекта из изображения необходимо провести предварительную обработку. Суть обработки заключается в вычислении вектора, значения элементов которого являются координатами объекта по оси x, а порядковый номер элемента - координатой по оси y. Перед началом обработки изображение разбивается на столбцы шириной 1 пиксель. Каждый срез представляет профиль изображения, пример профиля по координате y = 232 изображен на рис. 3. При этом координата по оси x представляет собой центр данного профиля.

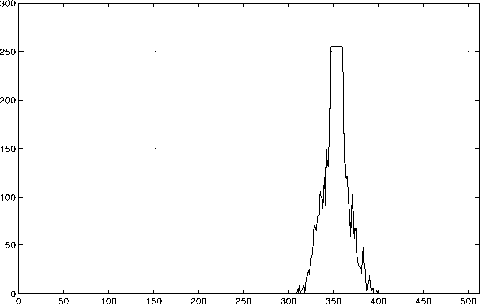
Рис. 3. Профиль изображения у = 232

В настоящее время существует несколько методов вычисления положения центра импульса, наибольшее распространение получили два из них: метод центра масс, медианный метод. Первый метод получил большее распространение, ввиду того что позволяет достичь субпиксельной точности без применения каких-либо дополнительных методов. Выражение для координаты центра импульса Хц запишем в виде:

ft./ГО

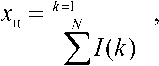
£=1

здесь к – номер пикселя в столбце, I (JP) – значе- ние его яркости.

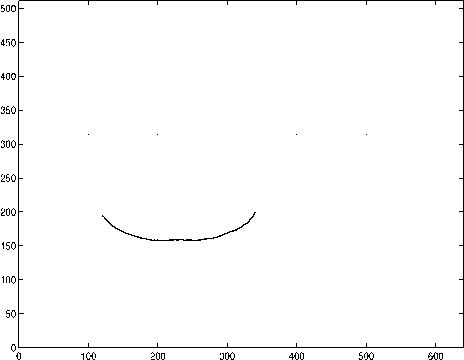
Рис. 4. Профиль объекта

Профиль объекта, координаты которого вычислены исходя из формулы (2), представлен на рис. 3. Необходимо отметить, что вид данного профиля отличается от полукруга, так как в данном случае идет речь не об абсолютных координатах, а о пиксельных.

Как уже отмечалось выше, лазерная триангуляция обладает достаточно высокой степенью точностью измерений по оси x (точность по y не превышает пиксельное разрешение), поэтому оценим величину минимально достижимой абсолютной погрешности ^■min в случае полностью когерентного источника. Для этого будем рассматривать столбец изображения, по которому делается оценка положения Хц , как некую двумерную область D [3]. Тогда выражение для Хц примет вид jj/(x,y) -xdxdy

’             0)

^Kx,y>dxdy

D где I(x,y) – значение яркости элемента dxdy. Абсолютную погрешность определим как среднеквадратичное отклонение случайной величины, то есть ^„. =.№-!■ Расположим центр декартовой системы координат в точке, где математическое ожидание случайной величины ^ц равно нулю, тогда дисперсию можно записать в виде

С учетом комплексного когерентного фактора Ma , введенного в [1], часть выражения (6) можно записать в виде:

MU(xx,yx)-I(x2,y2^ =

= МЦ (x,, y, )]² (1 + |//_л (x,, y, , x₂, y₂ )|²). (7)

Введя замену Ax = Xj-x₂, Ay = y!-y₂ и проведя преобразования координат, выражение (7) можно получить как

+cc +co

ДА] = J J|//^(Ax,Aj)|2£ZAxt7Ay x j ^MVKxx,yx'5\1xx1dxxdy2 x—--------

A2

Для оптической системы с оптическим параметром a (в случае если оптическая система состоит из одной линзы, параметр a равен ее радиусу) первый интеграл в (8) можно записать в следующем виде:

j J// ,(Av, Ai’)2<:/Ar<:/Ai'=

DVXJ-M

jj/(x, y) • xdxdy

D ______________

^x^dxdy

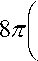
2- л-a-r) ' x

dx,

Как видно, знаменатель (4) представляет собой полную мощность, сосредоточенную в области D, и может быть представлен в виде:

здесь J\ (") – функция Бесселя первого рода; X – длина волны излучения; z – расстояние до объекта. С учетом свойства функции Бесселя jj/(x, y)dxdy = / jjdxdy, D                D

WiLaxA.

здесь I – среднее значение яркости по пятну D. С учетом (5) перепишем (4) в виде:

0(^1 =

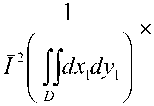
I j j jwu, , у,) • Цх2, y2)] • x, ■ x2dxxdyxdx2dy2 • выражение (10) запишется окончательно как

+X'+CC j J|//^(zAt,^y^dNxd^y =

(H)

Второй интеграл (8), положив, что математическое ожидание яркости равно усредненной яр-

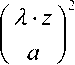
кости пятна, то есть w^,^)]^/,и переходя к полярной системе координат, можно получить в виде

J Jw(x,,^i ^x^dxyly.

D

2л-г0

J Jr3 cos2 (

f ^Гд x 2

4 Я"

V о о у

В итоге дисперсию в случае когерентного источника можно представить как

Az \ a 1

В случае одиночной линзы:

. a sint/ ® —, z

где sin и – апертура наблюдения. Минимально достижимая погрешность измерения расстояния до объекта для когерентного источника излуче- ния равна

Axmin

2 л sinw

.

При частично когерентном источнике излучения, что наиболее часто бывает на практике, ве- личина погрешности есть m,n 2 л sinu’

где C – безразмерная величина, определяющ а я контрастность спеклов, при этом Се(0,1), X – средняя длина волны излучения. Параметр C сильно зависит от типа облучаемой поверхности и может быть определен как

C²= , ¹ =, (17)

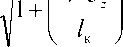
здесь 5_Z – величина шероховатости поверхности, I – длина когерентности, под которой понимается расстояние между двумя точками пространства, которое проходит свет лазера за время t_k , в течение которого пространственная разность фаз колебаний в этих точках остается постоянной.

Важную роль на практике параметр С начинает играть при облучении поверхности, структура которой неоднородна, в результате чего имеет место флуктуация С в широких пределах. При этом погрешность измерений резко возрастает из-за появления шумов спеклов. Физической природой данных шумов служит явление интерференции. При облучении объекта когерентным излучением каждая облученная точка объекта становится источником вторичных волн (принцип Гюйгенса), интерференцию которых мы видим в виде шумов на матрице. По своему виду шумы спеклов относятся к импульсным помехам.

Если подставить в (15)-(16) реальные значения, которые встречаются в реальных лазерных триангуляционных измерителях, то можно получить, что минимально теоретически достижимая погрешность может достигать значений порядка (100-200) X . Из-за наличия шумов спеклов реальные показатели куда хуже и составляют 0,05…0,1% от диапазона измерения. Основной проблемой является не столько погрешность, сколько повторяемость результатов измерений одной и той же поверхности при различных значениях, мощности излучения лазера и времени выдержки матрицы. Полученные на опыте данные показывают, что при изменении выдержки матрицы со 100 мкс до 800 мкс при неизменной мощности лазера положение профиля объекта (изображен на рис. 4) смещается на 1,2…2,5 пикселя. При рабочем диапазоне сканера в 250 мм с разрешением 512 пикселей по вертикали получается погрешность в 0,6…1,2 мм, что является для большинства приложений недопустимым. Основным источником, мешающим получить одинаковые результаты при различных выдержках матрицы, являются шумы спеклов.

2 Борьба с шумами спеклов методом слепой обработки изображения

В общем случае изображение g^,yy подвергшееся линейным искажениям, можно представить в виде свертки исходного изображения f(x,y) с функцией рассеяния точек (PSF – point spread function) [2] Kx,y^ и добавлением аддитивного шума n(x,y) :

g(x,y) = f(x,y) * Kx^ + n(x,y) . (18)

Шумы спеклов, которые вносят основную погрешность в системах лазерной триангуляции, по своей природе являются мультипликативными (т.е. имеют место только при наличии сигнала) и в данной модели содержатся в функции PSF. При этом мы не можем оценить функцию PSF в любой момент времени для применения классических подходов фильтрации. Следует отметить, что применение нелинейных алгоритмов фильтрации (медианный фильтр, усредняющий фильтр и т.п.), нашедших широкое применение в задачах обработки изображений, в случае лазерной триангуляции не всегда могут быть применены, так как их использование ведет к смещению оценки положения профиля объекта и как результат – к возрастанию погрешности измерения. В данном случае наиболее эффективным является методы слепого разделения сигналов (blind signal separation) на фоне шума, так как они не требуют знания функции PSF и при этом являются линейными.

На рис. 5 показана схема возникновения искажений на исходном изображения f(x,y). На выходе данной схемы мы имеем восстановленное изображение Rx,yY В идеальном случае Rx,y^ = j\x,yy но на практике это трудно достижимо из-за наличия аддитивного шума.

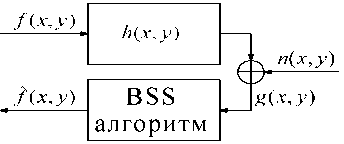
Рис. 5. Схема восстановления изображения

Приведем пример восстановления изображения, базирующийся на широко известном методе ZSS(Zero Sheet Separation), где в качестве критерия используется наибольший общий делитель (НОД). Перед началом обработки исходное изображение подвергается двумерному z -преобразованию:

height width

С(21,2₂)- £ ^g^H^n^-z;"¹ -zf², (19)

здесь height и width являются, соответственно, высотой и шириной изображения. Фактически выражение (19) определяет полиномиальную форму представления изображения.

С учетом линейности z -преобразования выражение (19) можно записать в виде

G(z,, z,) = F{z_} , z₂) • H(z_x , z₂) + N(z,, z₂ ) . (20)

Рассмотрим идеальный случай, при котором аддитивный шум отсутствует, то есть n^x, j?) = 0 ^> N(z_x , z₂) = 0. Тогда выражение (20) можно переписать в виде:

G(z_vz₂) = F(z₁,z₂)-H(z₁,z₂\   (21)

Исходя из выражения (21) можно сказать, что задача получения исходного изображения f(x,y) из g(x,y) сводится к задаче факторизации полинома Gvz,y Основной проблемой при этом является выбор критерия разделения полинома. В качестве критерия можно использовать критерий наибольшего общего делителя. Для этого возьмем два изображения одного и того же объекта так, чтобы выполнялось условие №,yv №,y") , но при этом hyx,yVhAx,y^ . Выполнения этих условий можно достичь съемкой объекта с малым интервалом времени, таким, что за этот интервал параметры освещенности и светопроницаемости среды не меняются. При этом мы получим систему уравнений с двумя уравнениями и тремя неизвестными:

Gi(zi,z2) = 77(z1,z2)-H1(z1,z2);

\С2(21,22) = ^(21,22).Я2(21,22). (22)

Из системы (22) интересующая нас функция Fx,zy> находится как НОД от G^z^z^ и G₂(z_pz₂) . В качестве алгоритма, применяемого для получения НОД, наиболее часто используется алгоритм Евклида. На рис. 6 представлен пример работы данного алгоритма, где в качестве исходных взяты два соседних изображения, полученных с триангуляционного сканера.

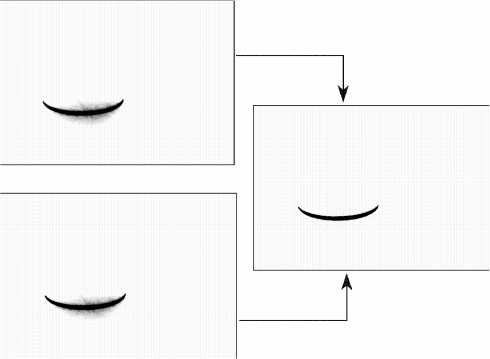
Рис. 6. Результат восстановления изображения

Как видно из рис. 6, шумы спеклов, видимые как ореол вокруг изображения, удалось подавить практически полностью. При этом при изменении выдержки матрицы со 100 мкС на 800 мкС профиль объекта смещается на величину не более чем 0,7 пикселя, что при диапазоне измерения в 250 мм и разрешении 512 пикселей по вертикали дает погрешность в 0,34 мм. Тем самым применение метода слепого разделения сигналов дает уменьшение погрешности измерения более чем в 7 раз.

Заключение

Задача определения геометрических параметров объекта, решаемая с помощью лазерной триангуляции, находит все большее применение в промышленности и на транспорте. Основной проблемой, мешающей внедрению, является разнородность оцениваемых поверхностей и как результат – неоптимальные условия работы сенсора, приводящие к возникновению шумов спеклов, что в конечном итоге приводит к увеличению погрешности. Применение слепой обработки позволяет уменьшить величину погрешности.