Применение спектральных методов обработки данных к результатам численного моделирования аттракторов внутренних волн

В отличие от атмосферы Земли, мировой океан не является классической тепловой машиной, и тепловые процессы вертикального обмена энергией, наряду с ветровыми воздействиями, играют существенную роль лишь у поверхности Океана. В тоже время существенное влияние на глобальную динамику Океана оказывают глубоководные процессы перемешивания, которые в настоящее время изучены в гораздо меньшей степени, как экспериментально так и фундаментально. Существенное влияние на глобальную динамику Океана оказывают глубоководные процессы перемешивания, которые в настоящее время как экспериментально так и фундаментально изучены в гораздо меньшей степени, чем приповерхностные явления, связанные с ветровым воздействием и теплообменом. В глубинах океана внутренние волны, возникающие из-за приливных течений и обтекания донного рельефа, могут сильно влиять на процессы вертикального перемешивания.

Открытые в 1995 году Лео Маасом [1, 2] аттракторы внутренних волн показали, что в определенных геометрических конфигурациях (которые как оказалось могут быть достаточно простыми) энергия внутренних волн может эффективно аккумулироваться вдоль определенных путей. После работ Лео Мааса аттракторам внутренних волн было посвящено большое количество исследований, в результате в настоящее время имеется достаточно развитая теория формирования аттракторов внутренних волн небольшой амплитуды.

Поэтому сейчас основной интерес исследователей вызывает поведение аттракторов внутренних волн большой амплитуды. При этом линеаризованные уравнения уже не описают поведение аттракторов, которые могут становится неустойчивыми, турбулентными, менять свою структуру с течением времени, оказывать существенное влияние на фоновую стратификацию и проявлять другие нелинейные свойства.

В Высшей нормальной школе Лиона в последние годы развиваются методики анализа данных экспериментов, связанных с внутренними волнами. Они позволили качественно и количественно описать ряд важных закономерностей при распространении внутренних волн, образовании и разрушении аттракторов [3].

Несмотря на успехи в экспериментальном изучении волновых аттракторах, в методиках определения параметров течений и гидродинамических полей имеется ряд существенных ограничений. Эти ограничения снимаются прямым численным моделированием. Но рассматриваемые явления обладают очень большим интервалом пространственных масштабов из-за большого числа Прандтля-Шмидта, поэтому такие исследования вплоть до последнего времени не были возможны и численное моделирование ограничивалось лишь линейными режимами, которые лишь подтвердили уже существующую теорию [4, 5]. Лишь недавно были проведено трехмерное прямое численное моделирование, полностью соответствующие экспериментам, и впервые гидродинамические поля экспериментов и расчетов соответствовали в пределах десяти процентов как для линейных, так и для нелинейных режимов [6, 7]. В настоящей работе мы применяем спектральные и статистические методы анализа гидродинамических полей к результатам численного моделирования к слабонелинейным режимам. В дальнейшем они позволят исследовать более сложные конфигурации и сильно нелинейные (турбулентные) режимы с перемешиванием.

2.    Математическая модель и прямое численное моделирование

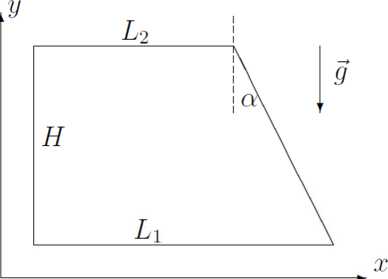
Рис. 1: 2D проекция расчетной области.

Fig. 1. 2D projection of the computational domain

Схема экспериментальной установки в двумерной проекции показана на рисунке 1.

В контейнере трапецеидальной формы находится раствор соли с постоянной по высоте частотой плавучести /V(z) =

-д йр№ „

——---. Соответственно соленость

PVZ) dz

распределена экспоненциально по высоте, но в условиях эксперимента она практически не отличается от линейного распределения. Можно показать, что условия эксперимента соответствуют предпосылкам использования приближения Буссинеска даже лучше, чем традиционные задачи конвекции. Поэтому полную систему уравнений можно записать в виде:

+ -i^VkU = -V— + z/Av + psg at              рт

+ vk Vkps = X^Ps, div(v) = 0

Граничные условия для скорости на боковых и нижней границах соответствуют условиям прилипания. На верхней границе ставится условие отсутствия вязких касательных напряжений. Для солености на всех границах ставится условие изоляции.

Левая граница совершает колебания следующего вида:

жь(0, у, t) = a cos(ny/H) cos(wot).

Прямое численное моделирование проводилось с помощью спектральноэлементного метода [8] и кода nek5000.

На рисунке 2 показаны примеры устойчивого аттрактора (слева) и неустойчивого (справа). Динамика горизонтальной компоненты скорости показана на рисунках 3,4.

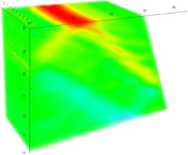
Рис. 2: Устойчивый и неустойчивый аттракторы. Цветом показана горизонтальная составляющая поля скорости.

Fig. 2. Stability and instability attractors. The colors show the horizontal component of the velocity field

N = 1.059, w₀ = 0.623, U_x in a point on the first ray 0.5

0.4 0.3 0.2 0.1

0 -0.1 -0.2 -0.3 -0.4 -0.5

10   20   30   40   50   60   70   80   90

Time in periods of the wall oscillation t/To,To = 10.0854.

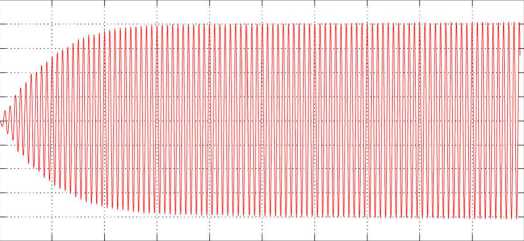
Рис. 3: Зависимость су от времени в точке на первом луче аттрактора.

Fig. 3. Dependence Vr on time at a point on the first ray of the attractor

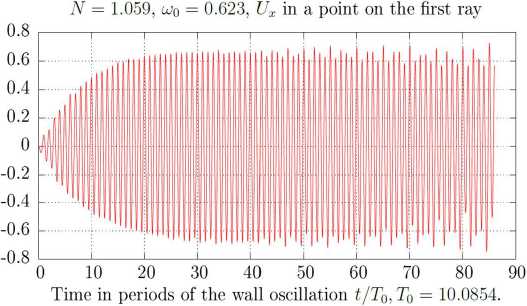
Рис. 4: Зависимость v_x от времени в точке на первом луче аттрактора. Слабая неустойчивость аттрактора.

Fig. 4. Dependence Vx on time at a point on the first ray of the attractor. Weak attractor instability’.

3.    Применение спектральных методов дляописание неустойчивости и процессов перемешивания

Для выявления имеющихся частот в системе построим частотно-временную диаграмму, а для проверки выполнения условий триадного резонанса на дочерние волны построим так называемый биспектр, отложив по горизонтальной и вертикальной осям частоты, при этом цвет на диаграмме пропорционален произведению соответствующих амплитуд.

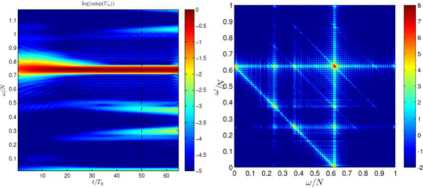
Рис. 5: Частотно-временная диаграмма и биспектр для слабонеустойчивого аттрактора

Fig. 5.Time-frequency diagram and bispectrum for weakly unstable attractor

Частотно-временная диаграмма позволяет увидеть появление вторичных частот й)!, <у₂, а биспектр доказывает выполнение соотношений ш₀ = а>₁ + <у₂, поскольку дочерние частоты лежат на антидиагонали квадрата, с основанием, равным родительской частоте. Применение подобной техники к результатам DNS также позволит исследовать каскады триадных резонансов процессы перемешивания и динамику спектра на длительных временах.