Применение средств вычислительной газодинамики для математического моделирования

Современное инженерное проектирование трудно представить без инструментов для решения задач моделирования течения жидкости и газа. В подобных программных продуктах лидирующее положение занимает метод конечных объемов (МКО), который заключается в том, что расчетная область разбивается на элементарные объемы, и дифференциальное уравнение в краевой задаче заменяется интегральными балансными соотношениями для каждого из этих объемов. После этого интегралы в соотношениях аппроксимируются с использованием значений искомой функции в узлах сетки или значений производных искомой функции, взятых из краевых условий. В результате получается система линейных алгебраических уравнений, решением которой является вектор значений искомой функции в узлах сетки. Данный метод отличается точностью и устойчивостью решения.

По сравнению с реальным экспериментом математическое моделирование можно выполнить в гораздо сжатые сроки , а получаемые результаты дают полную картину физического процесса в любой точке исследуемого объекта.

Далее будут рассмотрены программы подготовки сетки конечных элементов как часть автоматизации процесса проведения математического моделирования приемников воздушных давлений (ПВД) и других зондовых средств восприятия воздушных давлений [1], а также приведены результаты экспериментальных исследований и математического моделирования с применением как коммерческих, так и opensource программ.

ЭТАПЫ ПРОВЕДЕНИЯМАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Для получения результатов математического моделирования с приемлемой точностью требуется соблюдать определенный порядок действий с учетом проведенных ранее исследований. Проведение математического моделирования чаще всего можно свести к следующим этапам:

• -    подготовка геометрической модели;

• -    подготовка сетки конечных элементов;

• -    подготовка расчетной модели;

• -    проведение расчета;

• -    анализ результатов.

Безусловно, на каждом этапе свои требования и критерии получаемого результата, но в данной работе наибольший интерес представляет этап подготовки сетки конечных элементов. Для вычислительной газодинамики одним из наиболее важных критериев является разрешение вязкого подслоя для правильного моделирования пограничного слоя у стенок обтекаемого объекта (так называемый параметр y+ является показателем качества сетки в пограничном слое, значения которого приблизительного соответствуют вязкому подслою y+ < 3, логарифмическому слою 30 < y+ <300.). При создании тетраэдральной сетки наибольшее распространение получил способ создания призматического слоя для моделирования пограничного слоя.

ОБЗОР СРЕДСТВ ПОДГОТОВКИ СЕТКИ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Как правило, коммерческие проекты (например, Ansys [2]) интегрируют в своем составе всё больше средств моделирования, и становятся универсальными, хотя еще встречаются узкоспециализированные, которые имеют возможность сопряжения с аналогичными программами, например, FlowVision [3]. Для open-source проектов характерна также узкая специализация, даже мощный инструмент OpenFOAM [4] нацелен только на выполнение расчетов.

Рассмотрим по очереди наиболее распространенных представителей из классов коммерческих и открытых программ.

Пример реализации сетки в программе FlowVision с адаптацией по поверхности исследуемого тела представлен на рис 1.

Отличительной особенностью этой программы является уникальная технология «подсеточного» разрешения, где каждый элемент сетки, пересекающийся с моделируемым объектом, представляет собой сложный геометрический объект. Кроме того, есть возможность адаптации сетки (т.е. деление на более мелкие элементы) в зависимости от требуемых параметров.

Аналогично работает инструмент snappyHexMesh из состава OpenFoam, который также создает прямоугольную сетку конечных элементов, которую затем адаптирует под моделируемый объект. Пример сетки конечных элементов с призматическими слоями, созданной при помощи утилиты snappyHexMesh, приведен на рис. 2.

Следует отметить, что чаще всего open-source проекты нацелены на опытных пользователей, которые практически не замечают отсутствия графического, интуитивно-понятного интерфейса. Все настройки для создания сетки с помощью snappyHexMesh записаны в текстовом файле, созданную сетку можно посмотреть лишь с помощью сторонней программы, например, Paraview.

Ниже на рис. 3 и 4 приведены тетраэдраль-

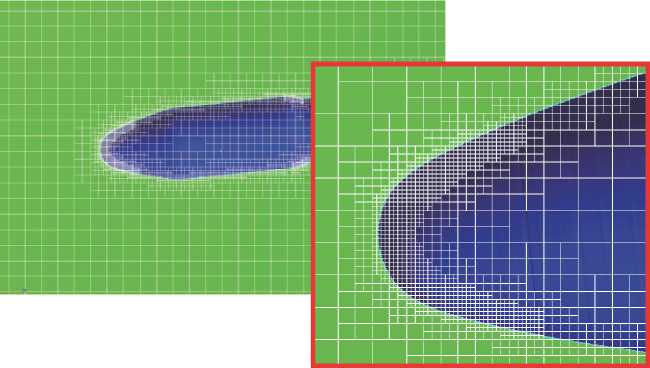
Рис. 1. Реализация сетки в FlowVision с адаптацией по поверхности

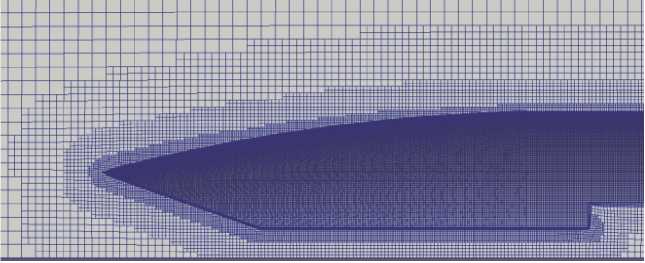
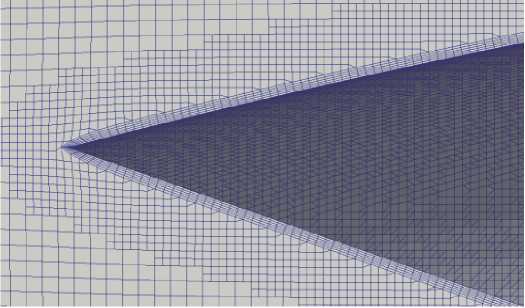
Рис. 2. Реализация сетки конечных элементов с призматическим слоем, подготовленная с помощью snappyHexMesh

Рис. 3. Реализация сетки конечных элементов с призматическим слоем в Ansys

File Geometry Mesh View Refinement Special Help Solve DemoApp

Quit | Generate Mesh | Stop |                                                                                      Visual | Solve | Recent | Mesh       —i | Zoom All | Center |

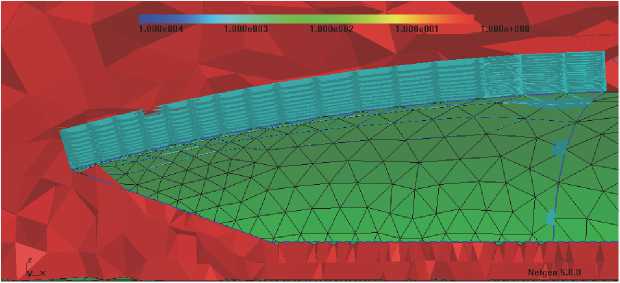
Points: 20846 Elements: 83824 Surf Elements 9152

Рис. 4. Реализация сетки конечных элементов с призматическим слоем в NetGen

ные сетки с призматическими слоями (высота призматических слоев увеличена для наглядности), подготовленные Ansys [2] и NetGen [5] соответственно.

Таким образом, предлагаемые подходы построения сетки конечных элементов одинаковы как в свободно-распространяемых программах (NetGen, EnGrid, Salome, gmsh и т. д.), так и в коммерческих программах (Ansys, Abaqus, Cosmos и т. д.).

Безусловно, при проведении математического моделирования обязательным является исследование на сеточную сходимость, т.е. чем меньше размер конечных элементов, тем точнее результат. Но на практике уменьшение размеров конечных элементов ведет к увеличению размерности сетки, и возникают вопросы потребления оперативной памяти и вычислительных ресурсов. Кроме того, на точность получаемых результатов влияет и выбор модели турбулентности [6-8].

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИЕМНИКА ВОЗДУШНЫХ ДАВЛЕНИЙ

Применение программ FlowVision и OpenFoam и оценку результатов математического моделирования рассмотрим на примере исследований приемника воздушных давлений с компенсационным контуром в виде гофриро- ванной поверхности. Исследуемый приемник приведен на рис. 5.

В аэродинамической лаборатории АО «УКБП» проведены экспериментальные исследования ПВД с компенсационным контуром в виде гофрированной поверхности. В одном случае отбор давления производился с помощью 8 отверстий диаметром 1.5 мм, в другом случае отбор производился щелью шириной 0.5 мм, имеющей вид кругового сектора. В обоих случаях использовались сменные насадки профилированного участка. Эксперименты проводились в диапазоне скоростей от 50 до 200 км/ч.

Математическое моделирование спектра обтекания рассматриваемого приемника проводилось на базе технологической платформы UniHUB [9]. При моделировании использовались модели турбулентности Shear Stress Transport (SST) и Spalart-Allmaras (SA). Параметры набегающего потока воздуха были следующими: давление невозмущенного потока – 101325 Па, температура равна +15°С, степень турбулентности потока – 1%. Можно отметить, что в силу отсутствия достоверных данных по величине турбулентности потока аэродинамической трубы при математическом моделировании принята низкая турбулентность набегающего потока.

Проведено математическое моделирование

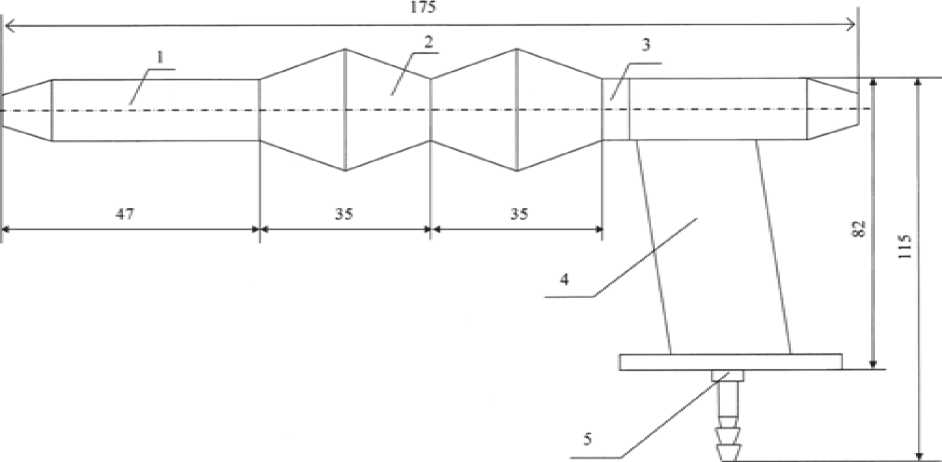
Рис. 5. Общий вид исследуемого макета непроточного ПВД:

1 – входной цилиндрический участок; 2 – профилированный участок; 3 – контровочная гайка; 4 – крепежный кронштейн; 5 – штуцер отбора статического давления

спектра обтекания рассматриваемого приемника с использованием программы Flow Vision версии 2.х [3]. В программе Flow Vision версии 2.x реализован метод конечных объемов, используется прямоугольная сетка с локальной адаптацией и подсеточным разрешением геометрии, что позволяет точно описывать области сложной геометрической формы. Кроме того, для повышения точности расчетов возможна адаптация сетки по форме границы расчетной области и динамическая адаптация к решению. Таким образом, получается расчетная сетка, достаточная для точного описания пограничного слоя вблизи стенок и в областях резкого изменения гидродинамических параметров. Для аппроксимации уравнений применяется конечно-объемный подход, позволяющий точно аппроксимировать законы сохранения на уровне отдельных ячеек. Итоговый метод решения уравнений Навье-Сток-са имеет второй порядок аппроксимации, что позволяет получать точные решения даже на грубой расчетной сетке. Сам метод решения уравнений Навье-Стокса широко известен, поэтому здесь он не рассматривается. Настройки модуля решения уравнений установлены по умолчанию. Расчетная сетка одинаковая для указанных моделей турбулентности.

Также проведено математическое моделирование с помощью программы Open FOAM, которая применяется для моделирования течения жидкости и газа. В основе кода лежит набор библиотек, предоставляющих инструменты для решения систем дифференциальных уравнений в частных производных как в пространстве, так и во времени. Рабочим языком кода является язык C++ [4]. В терминах данного языка большинство математических дифференциальных и тензорных операторов в программном коде (до трансляции в исполняемый файл) уравнений может быть представлено в удобочитаемой форме, а метод дискретизации и решения для каждого оператора может быть выбран уже пользователем в процессе расчёта. Таким образом в коде полностью инкапсулируются и разделяются понятия расчетной сетки (метод дискретизации), дискретизации основных уравнений и методов решения алгебраических уравнений. В процессе моделирования использовался решатель SimpleFoam – стационарная программа решения для турбулентного течения неньютоновой жидкости. При вычислении не учитывались шероховатость поверхности и крепление приёмников к поверхности летательного аппарата. Исходными данными для математического моделирования являлись скорость потока, угол между направлением потока и осью макета ПВД, а также плотность воздуха в соответствии с проведенными экспериментами. Использовалась тетраэдральная сетка с призматическим слоем вблизи поверхности приемника для учета пограничного слоя. В целом параметр y+ не превышал 1, что является показателем правильного описания процессов в пограничном слое. Проводилось сравнение результатов моделирования с данными, полученными после эксперимента.

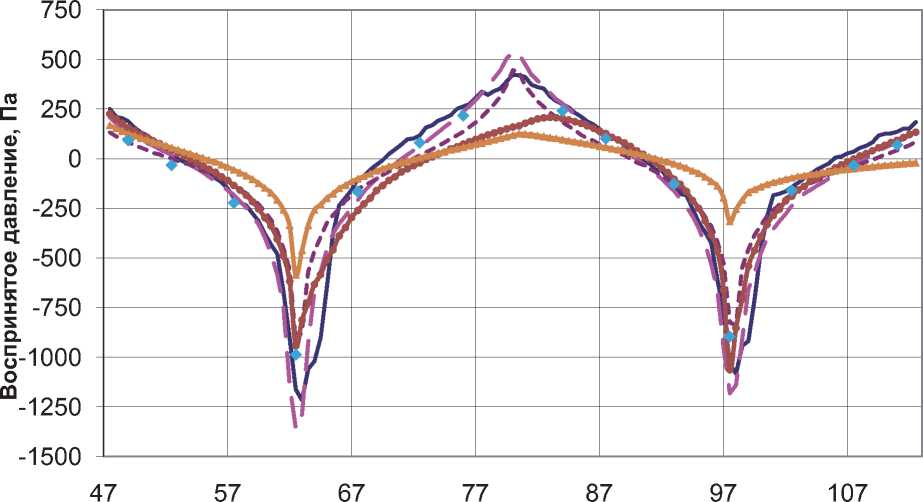
На рис. 6 показано распределение давления по длине профилированного участка приемника (приведены результаты эксперимента и математического моделирования: «щель» – соответствует случаю отбора давления щелью, «отв.» – соответствует случаю отбора давления отверстиями, «FV SST» – математическое моделирование с

Длина приемника, мм

-----щель                     ♦ отверстие              --FlowVision (SST)

FlowVision (SA)              Open Foam (SST)            Open FOAM (SA)

Рис. 6. Распределение давления по длине профилированного участка при скорости набегающего потока 200 км/ч

использованием SST-модели турбулентности программе Flow Vision, «FV SA» – математическое моделирование с использованием SA-модели турбулентности программе Flow Vision, «OF SST» и «OP SA» соответственно в программе Open FOAM ). Длина приемника отсчитывается от носовой части, все воспринятые давления приведены в Паскалях относительно давления невозмущенного потока.

Как видно из приведенных выше результатов есть расхождение как между двумя проведенными экспериментами, так и между математическими моделями.

При анализе сходимости результатов исследования обращают на себя внимание следующие моменты:

• -    значительное расхождение наблюдается на задних гофрах, где возможно образование вихрей;

• -    ввиду того, что диаметр отверстий для отбора давления составляет 1.5 мм, происходит некоторое усреднение давления на этом участке;

• -    отсутствует достоверная информация о величине турбулентности потока в аэродинамической трубе.

ЗАКЛЮЧЕНИЕ

В данной работе кратко рассмотрены вопросы создания сетки конечных элементов с использованием коммерческих и open-source программ. Отмечено, что коммерческие программы наце- лены на обычного инженера, который в сжатые сроки должен проводить большой объем исследований, поэтому важно предоставить инструмент с интуитивно-понятным графическим интерфейсом. Open-source программы, изначально ориентированные на энтузиастов и академических исследователей, уже практически не уступают по имеющемуся функционалу и развитие технологических платформ [9] свидетельствует об увеличении интереса к open-source проектам.

Результаты сравнения показали, что часть экспериментальных исследований при проектировании приемников воздушных давлений может быть заменена математическим моделированием с использованием либо коммерческих программ типа FlowVision, либо программ с открытым исходным кодом типа OpenFoam.