Применение статистических методов в прогнозировании урожайности зерновых культур на примере Волгоградской области

В Российской Федерации зерновое производство считается основой агропромышленного комплекса. На территории Волгоградской области аграрное производство также является одним из основных направлений хозяйственной деятельности. АПК региона создает более 10% валового регионального продукта [2,4].

Несмотря на предпринятые меры правительством и органами управления АПК, агропромышленное производство страны все еще не преодолело затяжного кризисного состояния, вызванного социальноэкономическими преобразованиями1990-х годов. Формирование многоукладной аграрной экономики само по себе не позволило решить проблемы сельского хозяйства [3,6]. В связи с этим обеспечение продовольственной безопасности требует построения достоверных прогнозов развития аграрного производства, основанных на экономикостатистических моделях, описывающих статистические зависимости исследуемого экономического показателя от основных факторов, оказывающих на него существенное влияние [5].

Прогнозирование-это предсказание будущего на основании накопленного опыта и текущих предположений относительно него. В настоящее время следует отметить непрерывно растущую потребность в прогнозах.

Прогнозирование представляет собой сложный процесс, по ходу которого необходимо решать большое количество различных вопросов. Для его производства следует применять в сочетании различные методы прогнозирования, которых на сегодняшний день существует огромное множество, но на практике используется значительно меньше.

Методы, получившие наиболее широкое распространение в мировой практике, это метод экспертных оценок, моделирование и прогнозирование (рисунок 1).

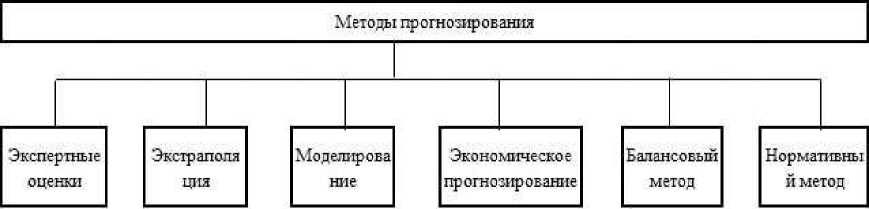
Рисунок 1 Методы прогнозирования

Метод экспертных оценок используется, как в нашей стране, так и за рубежом для получения прогнозных оценок развития производства, научнотехнического прогресса, эффективности использования ресурсов и т.п.

Нормативный метод является наиболее трудоемким, так как на практике установление идеальных норм и нормативов достаточно сложный процесс.

Необходимым условием регулирования рыночных отношений является составление надежных прогнозов развития социально-экономических явлений.

Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, т.е. для определения ориентировочных размеров явлений в будущем. Для этого используется метод экстраполяции. Метод прогнозной экстраполяции с точки зрения возможности применения на различных уровнях хозяйствования обладают большей универсальностью.

Дополнительным преимуществом является отсутствие необходимости в расчете большого количества входных параметров для построения прогноза. Информационной базой для построения прогноза являются наблюдения значений изучаемого показателя в длительной динамике. Выбор типа модели зависит от цели исследования и основывается на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики. Простейшими моделями, выражающими ~ тенденцию развития, являются: линейная функция:   yt а +  вt;

~ показательная функция: ^{y t}  а*вt ;

~ степенная функция: yt   а + вt + сt2 .

В данном случае, для прогнозирования урожайности зерновых культур методом экстраполяции, на примере Волгоградской области, воспользуемся линейной моделью. Расчет параметров функции выполним методом наименьших квадратов, в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими ~                      ~ уровнями: Σ ( yt - yi)2 стремится к min, где yt - выровненные уровни, yi – фактические уровни. Параметры «а» и «в» согласно методу наименьших квадратов находятся решением система нормальных уравнений: т.к. в обоих случаях Σt = 0, система нормальных уравнений примет вид:

£ У = na

^{£ y}t = в ^£ t   вычислив параметры а = 7,76; в = 0,029 можем

~ представить трендовую модель искомой функции в форме yt 17,76 + 0,029 t.

~

Так на основе исчисленного уравнения ^{y t} 17,76  +  0,029t.

экстраполяцией при t = 16 можно определить ожидаемую урожайность

~ зерновых культур в 2016 году ц/га: yt   17,76 + 0,029*16 = 18,221 ц/га. Так как на практике результат экстраполяции прогнозируемых явлений обычно получают не дискретными, а интервальными оценками, для определения ~      ~  ~      ~ границ интервалов воспользуемся формулами: y t  + taS yt ; y - taS y

.где: tα – коэффициент доверия по распределению Стьюдента;

Таблица 1 - Выравнивание по прямой ряда динамики урожайности зерновых культур

Годы	Урожайность, ц/га	t	t2	yt	~ y t	yi - ~ y t	~ (yi - y t )2
2001	17,9	-13	169	-2321,7	17,38	0,52	0,2704
2002	17,5	-11	121	-192,5	17,44	0,06	0,0038
2003	15,0	-9	81	-135	17,50	-2,50	6,2302
2004	17,7	-7	49	-123,9	17,55	0,15	0,0213
2005	18,3	-5	25	91,5	17,61	0,69	0,4732
2006	16,9	- 3	9	-50,7	17,67	-0,77	0,5931
2007	17,8	- 1	1	-17,8	17,73	0,07	0,0052
2008	24,6	+ 1	1	24,6	17,79	6,81	46,4285
2009	19,2	+ 3	9	57,6	17,84	1,36	1,8383
2010	12,0	+ 5	25	60	17,90	-5,90	34,8359
2011	17,2	+ 7	49	120,4	17,96	-0,76	0,5779
2012	16,4	+ 9	81	147,6	18,02	-1,62	2,6187
2013	17,5	+ 11	121	192,5	18,08	-0,58	0,3321
2014	20,6	+ 13	169	267,8	18,13	2,47	6,0797
Итого	Σy =248,6	Σt = 0	Σt2=91 0	Σyt=26,4	~ y t = 248,6	~ yi - y t = 0	(yi - ~ y t )2 = 100

Источник: авторский по [1]

~~

S yt =  √Σ(yi -  yt )2/(n-m) – остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели ~ тренда. Вероятностные границы интервала прогнозируемого явления: ( yt -~~ tαS yt ) ≤ упр ≤ ( yt + tα S yt )

Рассчитаем прогнозируемые доверительные интервалы урожайности зерновых культур на 2016 г. При n = 2 и m = 14, число степеней свободы равно 12. Тогда при доверительной вероятности, равной 0,95, коэффициент ~ доверия tα = 2,1718 (по таблице Стьюдента), (yi - yt )2 = 100

Тогда S ~yt = √ 100,00 / 12 = + 2,89; - 2,89. Зная точечную оценку ~ прогнозируемого значения урожайности:  yt  18,221 ц/га определяем вероятностные границы интервала по формуле:

18,221 ц/га.– 2,1718*2,89 ≤ упр ≤ 18,221 ц/га.+ 2,1718*2,89

11,94 ≤ упр ≤ 24,50.

Следовательно, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в 2016 году не менее чем11,94 ц/га, но и не более чем 24,50 ц /га.

Нужно иметь ввиду, что экстраполяция в рядах динамики носит не только приближенный, но и условный характер. Поэтому ее следует рассматривать как предварительный этап в разработке прогнозов. Для составления прогноза должна быть привлечена дополнительная информация, не содержащаяся в самом динамическом ряду.