Применение степенных рядов к решению практических задач

Ряды – одно из основных понятий математического анализа. С помощью рядов можно решать огромный спектр математических задач: вычислять интегралы, находить приближенные значения, применять к решению дифференциальных уравнений, а так же решать другие прикладные задачи.

Чаще всего при решении задач точное выполнение указанных математических операций оказывается весьма затруднительным или невозможным. В этих случаях приближенное значение можно получить при помощи рядов с любой точностью, достаточной для практического использования. Ряды – это простой и совершенный вычислительный инструмент, который не уступает любому механизированному средству вычисления. Также на теории рядов основываются дифференци-

альное и интегральное исчисления, так как ее алгоритмы и положения абсолютно необходимы при работе с физическими явлениями и физическим миром. Поэтому знание теории рядов и умение прилагать их к решению практических задач просто необходимо для студентов.

Рассмотрим применение степенных рядов к решению практических задач. А именно: применение рядов к приближенным вычислениям, к решению дифференциальных уравнений и применение рядов к приближенным вычислениям определенных интегралов.

Степенные ряды используются из-за их несложности применения в абсолютно всех разделах математики, физики, а также иных наук.

Степенным рядом называется ряд вида:

а₀ + а 1 (х-х₀) + а₂(х-х₀)² + ••• + а _п(х-х ₀)ⁿ = S n=о ^а п (х — х о )^п,  (1)

где а0, а-^ а2,..., ап,... —постоянные числа, называемые коэффициентами ряда, х0 —фиксированное число.

В     частности,     если     х0 = 0,     то     получаем     степенной     ряд:

а₀ + а ₁х + а₂х² + а₃ х³ + —+ а_пх^п = £ П= ₀ а_пх^п, который всегда сходится при х = 0.

Об области сходимости степенного ряда можно судить, основываясь на следующей теореме.

Теорема Абеля.

Если степенной ряд:

Z" оап(х-х0)п (2)

сходится в некоторой точке х=х ≠х , то он сходится абсолютно для всех х, таких, что |х-х |<|х -х |. Если степенной ряд расходится в точке х=х ≠х,то он расходится при любом х, для которого |х — х₀| > |х 2 -х₀| [1].

Приближенное вычисление корней

Вычислить приближенно с точностью до 0,0001 значение корня: Ve.

Решение:

Для приближенного вычисления Ve используем разложение функции ех = 1 + — + — + хп                                          1

—+ — + — (—то <  х < то), полагая х = -:

е =1+ ⁴ + 1!

3!

5!

111  1   1

1+4+32+384+6144+122880+⋯

Шестой член разложения      < 0,0001, значит, для заданной точности достаточно найти сумму пяти первых членов разложения сходящегося ряда:

4Г √е

1+4+32+384+

1,2840․

Приближенное вычисление логарифмов

Вычислить приближенно с точностью 0,001: ln3,5.

Решение:

Воспользуемся формулой ln =2 х+ +⋯+    +⋯ разложения ln , вычислим предварительно значе ние х.

1+х

1-х

=3,5

3,5(1-х)=1+х

-4,5х = -2,5 5

х=9․

Подставим найденное значение х в разложение.

ln3,5 = ln

1+ ⁵ ₉

=2∗

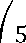
55  5

9+3∗9 +5∗9 +

9+

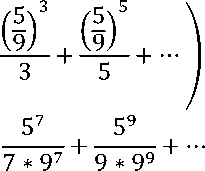
Так как пятый член разложения ∗  ≈ 0,0006 < 0,001, для удовлетворения заданной точности достаточно вычислить сумму первых четырех слагаемых разложения:

ln3,5 ≈ 2 ∗ (0,5556 + 0,0572 + 0,0106 + 0,0023) ≈ 1,251 [2].

Применение рядов к приближенным вычислениям определенных интегралов

Разлагая подынтегральную функцию в ряд Маклорена и интегрируя его почленно, найти разложения в ряд следующего интеграла: ∫sinх2 dх․

Решение:

гт „ Г

Для разложения ∫ sinх dх воспользуемся рядом Маклорена для sinх=х- +  -

⋯+(-1)       +⋯(-∞<  <∞), заменив в нем х на х :

х⁶ х 10                    х 4п—2

sinх 2 =х2-х3!+х5! -⋯+(-1)   (2n-1)!+⋯․

Почленно интегрируя, получим искомое разложение:

∫ sinх2dх=  -    +

X11

X15

-

5!∗11    7!∗15

+⋯+С [3].

Применение рядов к решению дифференциальных уравнений

Найти частное решение y(x) дифференциального уравнения, удовлетворяющее начальным условиям: у ' =3ех -у2cosх, у(0) =1․

Решение:

Найдем несколько первых членов разложения в ряд частного решения дифференциального уравнения первого порядка :у' =3ех -у2 cosх. Так как по условию хQ =0, искомое частное решение y(x) можно записать, используя разложениеу(х) = у(хQ)+  ( )(х- х о )++у" (S)(х-х о )2+⋯+у- (- )( 52)(х-х о )п+ ⋯,так: у(х) =у(0) ++у' (- )х+ у". (! - )х 2+ ⋯+1(- )( 2 )х п + ⋯(*) !

Найдем у(0), у ' (0)․

По условию y(0)=1. Значение у ' (0) найдем, подставив в данное уравнение начальные условия: у ' (0) =3е0-12 соs0 = 2․Последовательно дифференцируя данное уравнение и подставляя х==хо =0, найдем у " (0), у (0):

у " =3ех-2уу 'cosх+у2 sinх; у"(0) =3е0-2∗1∗2соs0+12sin0 = -1․ у  =3ех-2(у ')2 cosх - 2уу " cosх + 2уу' sinх + 2уу'sinх+у2 cosх; у (0) =3е0-2∗22∗cos0-2∗1(-1)соs0+4∗1∗2sin0+ +12соs=-2․

Подставим найденные коэффициенты в разложение (*).

Получим искомое частное решение:

у(х)=1+I_-i_- ²-i ; +⋯ или у(х)=1+2х- - +⋯. [4]

Таким образом, были рассмотрены примеры, которые чаще всего встречаются

при изучении математических дисциплин. Это лишь малая часть тех задач, которые

можно решать с помощью степенных ря-   теория рядов служит надежным инстру- дов. Таких задач огромное количество и    ментом для их решения.