Применение стробоскопического отображения Пуанкаре для диагностирования дефектов узлов сопряжения роторной системы

Введение. Большинство механических систем в своем составе имеют узлы, совершающие вращательные движения. При стационарном режиме функционирования (неизменные угловые частоты) данных узлов такой вид движения характерен тем, что координаты состояния таких систем являются периодическими функциями времени или пространственных перемещений. Факторы, вызывающие периодические вариации координат состояния, разнообразны. При обработке на металлорежущих станках – это разнообрабатываемость, вызывающая погрешности формы поперечного сечения. При рассмотрении качества роторных фрикционных систем – это развитие неравномерности износа по периоду вращения. К таким же эффектам приводит дисбаланс роторных систем. Эта особенность позволяет сделать вывод о том, что проявления возможных дефектов данных узлов также будет носить характер, близкий к периодическому. Таким образом, задача диагностики работоспособности системы может быть сведена к восстановлению периодических состав- ляющих в выходном сигнале и анализе причастности тех или иных механизмов к их формированию.

Рис.1. Модель рассматриваемой системы

Математическая модель роторной системы. Рассмотрим модель ротора, взаимодействующего со статором через трибосреду. Вращение данного ротора осуществляется посредством двигателя постоянного тока (рис.1).

Математическая модель данной системы в форме Коши может быть представлена в следующем виде:

.= ( UC.-. IR a )

L a

= ( ^ICm - ^M ( x 1 , x 2 , « ) )

Ш        J a = to

( F x ( x 1 , x 2 , ^a)^{- V} 1 h )

m

.    ( ^Fy ( x 1 , x 2 , ^a)^{- V} 2 h )

V2 =------------------- m x1 = V1

x 2 = V 2

где C_e , C_m , R_a , L_a – параметры двигателя постоянного тока; h – коэффициент диссипации;

g - ускорение свободного падения; a - угол поворота ротора относительно статора;

x 1 ,x 2 - координаты ротора относительно центра статора; F_x ( x 1 , x 2 , а ) , F y ( x 1 , x 2 , а ) , M ( x 1 , x 2 , а ) - силы и момент, формируемые трибосредой при взаимодействии ротора со статором (см. ниже).

Силы и момент F_x ( x 1 ,x 2 , а ) , F y ( x 1 ,x 2 , а ) , M ( x 1 , x 2 , а ) возникают в результате взаимодействия отдельных элементов поверхности ротора и статора. Причем степень взаимодействия зависит от взаимной удаленности этих поверхностей и скорости их движения друг относительно друга. Удельная сила взаимодействия может быть разложена на две составляющие: тангенциальную и нормальную. Функция, характеризующая зависимость удельной силы взаимодействия от взаимной удаленности, называется функцией сближения (рис.2).

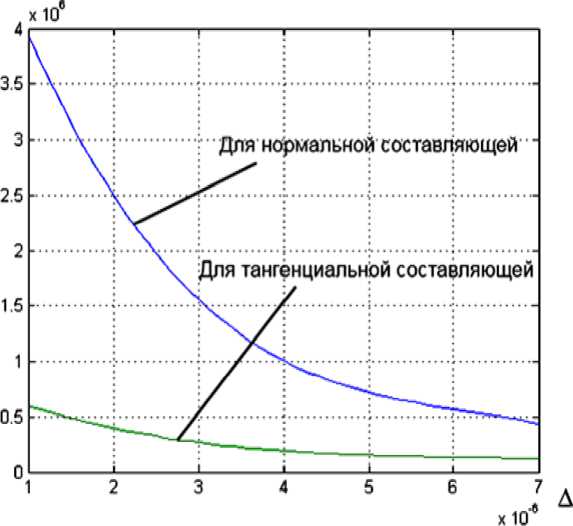
Рис.2. Пример функций сближения

Если аппроксимировать функцию сближения полиномом третьего порядка, то зависимость тангенциальной и нормальной составляющей удельных сил от взаимной удаленности А можно будет записать в следующем виде:

33 P n ( А ) = ^ П А ;     P ( А ) = £ х t A .

= 0                              г = 0

После интегрирования по взаимодействующей поверхности могут быть получены значения: F _x ( x 1 ,x 2 , а ) ; F y ( x 1 ,x 2 , а ) , M ( x 1 , x 2 , а ) . Для этого необходимо задать функцию А ( ^ ) .

Дефекты статора и ротора могут быть представлены как периодические функции f 1 ( v ) и f , ( v ) соответственно (рис.3, а ). Сдвиг ротора относительно центра обозначим как г 1 . Совокупность f , ( v ) , f ₂ ( v ) и г 1 определяют функцию A ( v ) .

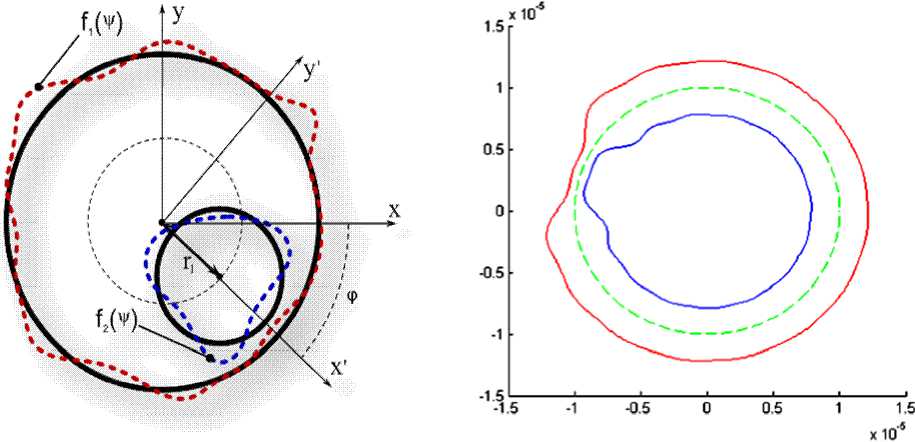
а )                                                           б )

Рис. 3. Ротор и статор: а – общий случай; б – пример ротора и статора с дефектом в форме импульса

Функции f . ( v ) и f 2 ( v ) могут быть представлены в виде ряда Фурье в тригонометриче-

ской форме с коэффициентами разложения C '' _k и C ' _k соответственно. Тогда с учетом вышесказанного силы будут:

F x ( x 1 , x 2 , а ) = F x cos Ф — F y sin Ф ,

F y ( x₁ , x ₂, a ) = F x sin ф + F y cos ф , где ф определяется по формуле:

x ф = arctan—, x2

а силы имеют вид:

ю

( х с , +х, с — 1 ) + £ с , 1х 2 с _н+х , с —

^Fx = ^П r o

-1- i

^{+ х} 3 C — 1 —, , + к _| ⁾ 1 ;

ю

+ У ск х3с к 3 1—( i + к) к=—ю

V

Г

i =—ю

>7

з х3с—1—(,+к))| , >7

ю

F у = — j п г 0 ( х , с , — х , с — 1 ) + £ с , I х 2 с , — i

ˆ

V

i =—ю

— х ^, ₂ с _—

1 - i

ю

+ У Ск ^3 C к 3 1—( i + к) к=—ю

—

где r ₀ – радиус ротора.

Причем коэффициенты, входящие в формулы сил, образом:

могут быть найдены следующим

х, =х n + j х t, х, = х n — j х t, с'ке<(а—ф)+ с''ке-jф,     к ^±1;

с - _e^{j (а—ф)} + с« _е -^{j ф} + ZL ,   к = ± 1.

k              k 2

С учетом выше определенных коэффициентов момент сопротивления будет:

M ( x ₁, x ₂, а ) = 2 j п r ₀ ²

юю х' +хtq + У с I х2с, + У скх;с

0      10            i 2 — ,            к 3 — ( , + к )

V              i =—ю    V          к =—ю

Пример функционирования математической модели. Рассмотрим динамику системы для случая, когда дефект ротора и статора имеет форму импульса (рис.3, б ). Результаты моделирования с учетом шумов, возникающих при измерении, приведены на рис.4, а и 4, б .

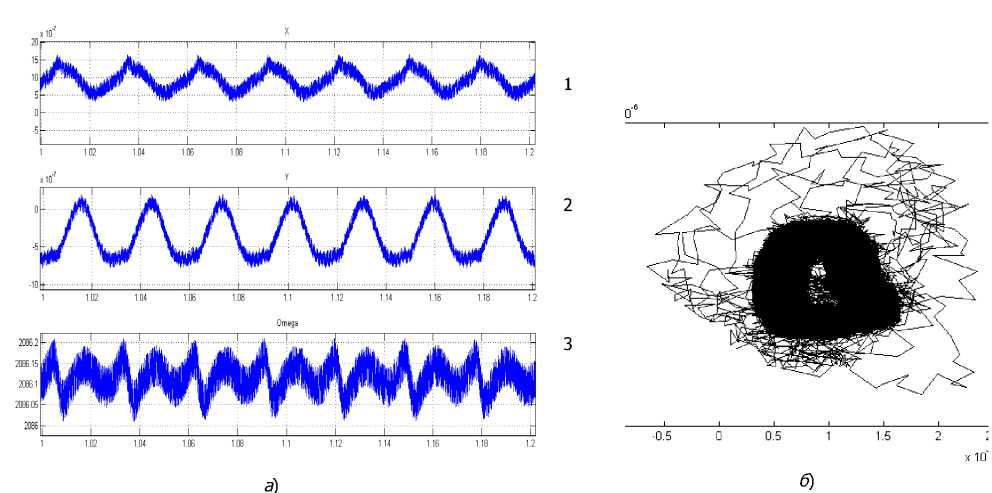
Рис.4. Результаты моделирования: a – 1 – колебания x ₁ , 2 – колебания x ₂ ,

3 – колебания угловой частоты вращения; б – движение ротора в плоскости x ₁ x ₂

Из рис.4, б видно, что анализ зашумленных результатов моделирования с целью диагностирования системы затруднителен. Поэтому необходима предварительная обработка данных. Стробоскопическое отображение Пуанкаре. Стробоскопическое отображение Пуанкаре [1] для динамических систем, имеющих периодическое решение, определяется как:

xn+1 = F ( xn , T ) , где T - период.

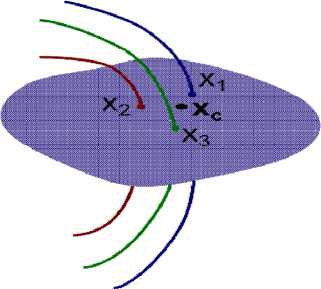
Рис.5. Стробоскопическое отображение Пуанкаре

Иначе говоря, формируется секущая плоскость в фазовом пространстве (рис. 5). Точки пересечения траектории движения с данной плоскостью (с некоторой ее локальной областью) образуют множество X = {x1,x2,^,xn}. Очевидно, что периодическое дви- жение образует множество из одинаковых точек.

Воздействие внешних помех приводит к варьированию точек множества в окрестности точки невозмущенного движения. Для широкого класса случайных возмущений справедливо следующее утверждение:

1n xc =  Z x , n i=1

где x_c – центральная точка этого множества, причем с ростом n центральная точка стремится к точке невозмущенного движения.

Таким образом, операция восстановления траектории невозмущенного движения может быть сведена к нахождению центральных точек при различных смещениях секущей плоскости вдоль траектории движения динамической системы. Назовем это операцией усреднения. Определим операцию усреднения функции F(t) с периодом т следующим образом:

- , х      ^Ц Fit + кт)F (t ) = lim У—(    )

n k = 0 n + 1

Для определения периода усреднения т воспользуемся теоремой [2].

Теорема. Среди множества функций F (t), почти наверное, наибольшими и равными ме- жду собой значениями средней за период T мощности

T

Р ( ^т ) = J F ( t ) ^dt

T ₀

обладают те и только те функции, для которых выполняется следующее равенство: т = Tn , где n е N .

Так как T неизвестно, можно использовать T ' >>  T . На рис.6 представлена зависимость средней мощности от периода усреднения.

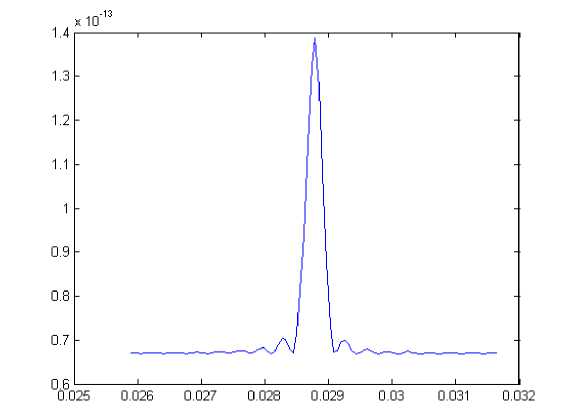
Рис.6. Зависимость средней мощности от периода усреднения

Применим операцию усреднения к ранее полученным результатам моделирования. На рис.7, а и б показаны восстановленные таким образом функции.

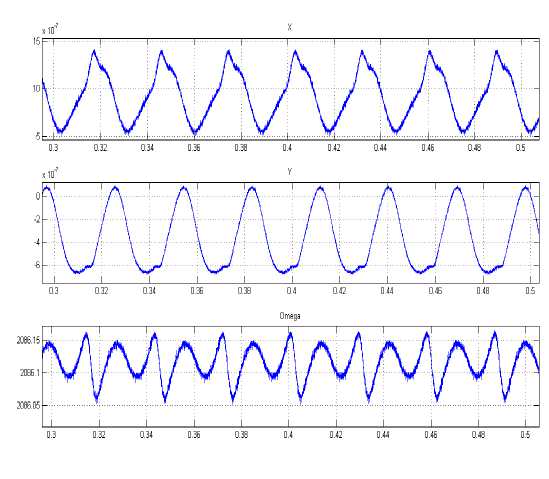
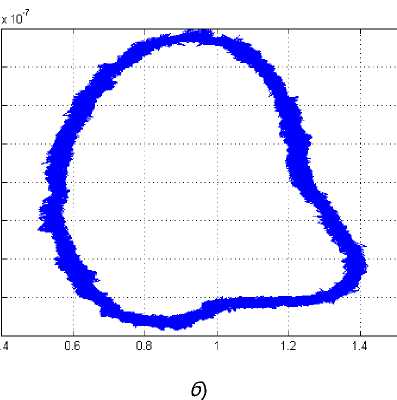
Рис. 7. Результаты усреднения: a – 1 – колебания x ₁ , 2 – колебания x ₂ , 3 – колебания угловой частоты вращения; б – усредненная траектория движения ротора в плоскости x ₁ x ₂

Выводы. Построенная модель роторной системы позволяет анализировать влияние пространственных неоднородностей узлов сопряжения на траекторию движения системы в фазовом пространстве, что в свою очередь, в также оценить отображение пространственной анизотропии на наблюдаемые (посредством датчиков виброакустической эмиссии или датчиков угла поворота) параметры движения, такие как, например, угловую частоту. Кроме того, предложенный алгоритм восстановления, основанный на стробоскопическом отображении Пуанкаре, позволяет выделять периодические составляющие в наблюдаемых параметрах, несущие информацию о дефектах узлов сопряжения. Это имеет важные значения: для обеспечения качества обработки деталей на металлорежущих станках и для виброакустической диагностики развивающихся по пространству дефектов в роторных системах (например турбинах).