Применение структурного подхода к распознаванию скелетов бинарных изображений

Несмотря на активное создание электронных коллекций графических документов (баз данных для хранения изображений), задача организации поиска в них является достаточно сложной и на сегодняшний день не решена до конца. На практике удается решить эту проблему только для определенных типов изображений [7].

При организации поиска требуется решить задачу распознавания изображений. В данной статье рассматривается применение структурного подхода к распознаванию с использованием скелетов. Структурные методы основаны на получении структурно-грамматических признаков, когда в изображении выделяются элементы – признаки и вводятся правила соединения этих элементов [8]. Анализ и сравнение получаемых последовательностей элементов разных изображений способствуют принятию решения. Такой подход обеспечивает высокое быстродействие, так как задача распознавания сводится к сравнению символьных структур, а не исходных изображений, что дает неоспоримое преимущество при решении задачи поиска в больших коллекциях графических документов.

ПОСТАНОВКА ЗАДАЧИ

Под бинарным изображением будем понимать черно-белую картинку в растровой решетке, на которой точки объекта черные (значение цвета равно 1), а точки фона – белые (значение цвета равно 0). В растровой решетке каждая точка имеет целочисленные координаты. Для оценки связности будем использовать 8-смежную структуру соседства [3], где соседними считаются точки, евклидовое расстояние между которыми 1 или √2. Множество точек называется связным, если любые две точки множества могут быть соединены последовательностью соседних точек, принадлежащих данному мно- жеству. Под дискретной фигурой (далее «фигура») будем понимать максимальное связное множество черных точек в растровой решетке, то есть такое множество, которое не содержится ни в каком другом связном множестве черных точек. Под «дырой» в фигуре будем понимать связное множество белых точек, окруженное точками фигуры. В описываемом алгоритме рассматриваются только бинарные изображения, содержащие одну фигуру без «дыр» (рис. 1а).

Точка фигуры называется граничной, если она имеет соседнюю точку, не принадлежащую фигуре [3]. Границей фигуры называется множество всех ее граничных точек (рис. 1б).

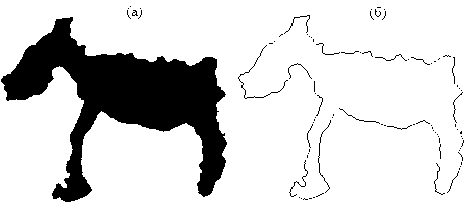
Рис. 1. Бинарное изображение (а) и его граничное представление (б)

Под скелетом фигуры в общем случае подразумевается множество центров окружностей, лежащих внутри фигуры и касающихся границы фигуры не менее чем в двух точках. Скелет можно рассматривать как граф [2] (рис. 2): его ребра – линии, состоящие из центров окружностей, касающихся границ в двух и более точках; вершины – центры окружностей, касающиеся границ в трех и более точках, а также крайние точки ребер. Вершина, имеющая одно инцидентное ребро, называется терминальной, более одного – узлом скелета. Ребро, инцидентное терминальной вершине, называется терминальным, остальные ребра – внутренними.

Однако с определением скелета фигуры на растровой решетке возникают трудности, связанные с тем, что здесь «не работает» понятие окружности. Поэтому строгого определения скелета растровой фигуры не существует. Однако существуют различные методы, позволяющие получить скелет растровой фигуры, близкий по своим свойствам скелету в общем случае. Поэтому под скелетом на растровой решетке в каждом конкретном случае подразумевают используемый для его получения метод. В данной работе используется алгоритм Зонга – Суня, о котором пойдет речь в следующем разделе.

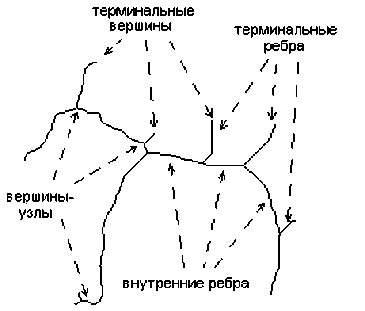
Рис. 2. Скелет бинарного изображения: сплошными линиями обозначен скелет, пунктирными со стрелками – указатели на элементы скелета

ПОЛУЧЕНИЕ СКЕЛЕТА ИЗОБРАЖЕНИЯ

Один из наиболее распространенных подходов к построению скелета растровой фигуры – класс методов топологического утончения фигуры [3]. Известно большое число реализаций этого подхода, отличающихся техническими нюансами. Идея данных алгоритмов состоит в последовательном утончении фигуры от границы к ее середине путем перекрашивания черных граничных точек в белые.

В разработанной системе реализован алгоритм Зонга – Суня [9], который является одним из наиболее быстрых алгоритмов топологического утончения фигуры. Он заключается в следующем: начиная с верхней левой точки в последовательности слева направо, сверху вниз просматриваются все точки изображения. Значения цветов исследуемых точек и их соседей обозначаются в соответствии с табл. 1.

Вводятся следующие переменные: А – число конфигураций 01 в последовательности P1, P2,

Таблица 1

Последовательность обозначения цветов исследуемой точки (P0) и ее соседей в алгоритме Зонга – Суня

P1	P2	P3
P8	P0	P4
P7	P6	P5

P3, P4, P5, P6, P7, P8, P1, то есть вокруг P0 существует только один переход от 0 к 1; B – количество 1 в последовательности P1, P2, P3, P4, P5, P6, P7, P8. Если выполняется: ((P0 = 1) И (2 <= B <= 6) И (A = 1) И (P2*P4*P6 = 0) И (P4*P6*P8 = 0)) или ((P0 = 1) И (2 <= B <= 6) И (A = 1) И (P2*P4*P8 = 0) И (P2*P6*P8 = 0)), то исследуемая точка перекрашивается в 0.

После достижения последней точки изображения просмотр начинается снова. Алгоритм заканчивается, когда за время очередного обхода не будет перекрашена ни одна точка. Непере-крашенные точки впоследствии образуют скелет.

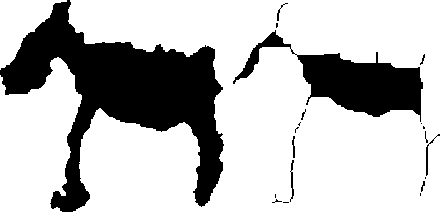
Пример работы данного алгоритма представлен на рис. 3.

(а)                                         (б)

(в)                                         (г)

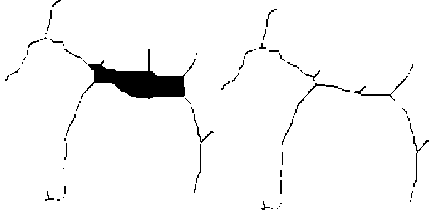
Рис. 3. Построение скелета фигуры с помощью алгоритма Зонга – Суня: (a) – исходная фигура;

(б) – 20-я итерация алгоритма, (в) – 40-я итерация алгоритма;

(г) – скелет фигуры, 62-я итерация алгоритма

РЕГУЛЯРИЗАЦИЯ СКЕЛЕТА

Обычно скелет фигуры содержит множество шумовых ребер, которые не являются существенными при описании общей формы фигуры (критерий несущественности будет определен ниже). Требуется их удаление, так называемая регуляризация скелета [2]. Появление подобных ребер связано с неровностями границы фигуры – в процессе топологического утончения в каждой выпуклости границы возникает новое терминальное ребро скелета, часто шумовое. Процесс регуляризации сводится к последовательному удалению шумовых терминальных ребер.

Предлагается алгоритм регуляризации, основанный на утверждении о том, что по скелету можно восстановить исходную фигуру, если для каждой точки скелета нарисовать круг с центром в этой точке и радиусом, равным расстоянию от нее до ближайшей точки границы фигуры. Данное утверждение вытекает из определения скелета в общем случае [3]. В связи с особенностями получения скелета на растровой решетке в нашем случае фигура восстанавливается приближенно.

Пусть F₀ – восстановленная по скелету фигура, а ее площадь – S 0 . Под площадью фигуры на растровой решетке понимается количество точек, из которых она состоит. Удалим какое-либо терминальное ребро i из скелета и снова восстановим фигуру, используя оставшиеся ребра и старые радиусы – расстояния до границ исходной фигуры (фигура F i ), обозначим ее площадь S i . Форма и площадь фигуры F i будет отличаться от фигуры F 0 . При этом если S i отличается от S 0 незначительно, то удаленное терминальное ребро является шумовым, так как не сильно повлияло (или вообще не повлияло) на площадь. Стоит отметить, что критерий сравнения площадей является достаточным, так как F i всегда будет лежать внутри F 0 .

Основываясь на данной идеи, предлагается следующий алгоритм регуляризации скелета:

• 1.    По скелету восстанавливается исходная фи

• 2.    Выбирается i-е терминальное ребро скелета.

• 3.    По скелету без ребра i восстанавливается фигура и считается ее площадь S i .

• 4.    Если S 0 - S i < P, где P – пороговая величина, то ребро i удаляется из скелета.

• 5.    Если остались нерассмотренные терминальные ребра – переход к п. 2, иначе конец алгоритма.

гура и вычисляется ее площадь S 0 .

Отметим, что в данном алгоритме в качестве терминальных рассматриваются только те ребра, которые были таковыми изначально, а не новые, появляющиеся при удалении ребер.

Пример работы данного алгоритма представлен на рис. 4.

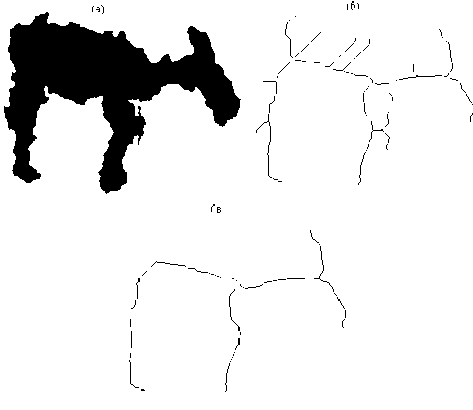
Рис. 4. Работа алгоритма регуляризации скелета:

(а) – исходное изображение; (б) – скелет; (в) – скелет после регуляризации

АППРОКСИМАЦИЯ СКЕЛЕТА

На данном этапе происходит аппроксимация ребер скелета прямыми линиями. Аппроксимация происходит с использованием метода последовательных приближений [1]. При этом в случае слабой кривизны ребра оно преобразовывается в одно ребро-отрезок с теми же вершинами, иначе ребро преобразовывается в набор отрезков. Кривизна ребра C измеряется максимальным евклидовым расстоянием от точек ребра скелета до аппроксимирующей его прямой. Если C > 0,2*D, где D – диаметр минимальной окружности, описанной вокруг скелета, то ребро заканчивается в точке максимума кривизны и далее скелет аппро-симируется от этой точки (рис. 5). Пороговое значение меры кривизны подобрано экспериментальным путем. Возможно, для некоторых классов изображений значение порога будет другим, поэтому при необходимости его можно изменить во время работы системы.

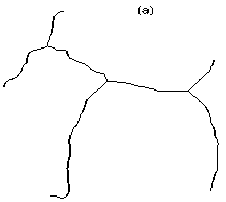
Рис. 5. Пример аппроксимации скелета: (а) – исходный скелет; (б) – аппроксимация скелета прямыми линиями

ПОЛУЧЕНИЕ ЦЕПОЧЕК ПРИМИТИВОВ

В качестве структурного описания скелета предлагается использовать цепочку примитивов, состоящую из прямых ребер аппроксимированного скелета и углов между ребрами. Предлагается следующий алгоритм получения цепочки для скелета, состоящего из n ребер:

• 1.    Произвольно выбирается терминальная вершина скелета и инцидентное ей терминальное ребро i = 1. Вторая, нетерминальная вершина, инцидентная ребру i, объявляется текущей.

• 2.    Вычисляется длина i-го ребра l i и записывается в цепочку.

• 3.    Среди ребер, инцидентных текущей вершине, выбирается то, которое составляет наименьший угол относительно i-го ребра против часовой стрелки (ребро i + 1). Рассматривается также само i-е ребро с углом, равным 360°.

• 4.    Угол α i между ребрами i и i + 1 записывается в цепочку.

• 5.    Если i + 1 = 2n + 1, то конец алгоритма. Иначе вершина, инцидентная ребру i + 1, не являющаяся текущей, объявляется текущей, i увеличивается на 1, переход на п. 2.

Примечание. Длина ребра является относительной величиной в процентах. За 100 % берется диаметр минимальной окружности, описанной вокруг скелета. Для поиска такой окружности используется алгоритм, предложенный в [4].

Получаемую таким образом цепочку можно записать в виде {l i , α i }, i = 1, . . . , 2n, где n – количество ребер скелета.

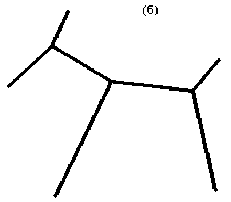
На рис. 6 представлен пример получения цепочки примитивов простейшего скелета. Здесь стрелками обозначено направление обхода скелета, 0 – точка, в которой начинается обход. Полученная цепочка имеет вид:

{70 ; 95} {50 ; 360} {50 ; 90} {40 ; 360} {40 ; 175} {70 ; 360}.

СРАВНЕНИЕ ЦЕПОЧЕК

Конечным этапом алгоритма распознавания является сравнение цепочек примитивов скелетов различных фигур между собой. Если цепочки похожи, то и скелеты, и фигуры, из которых они получены, также похожи.

Пусть имеются две цепочки длины 2n, описывающие разные фигуры:{l i , α i }, i = 1, . . . , 2n, {k i , β i }, i = 1, . . . , 2n.

Тогда введем следующее условие равенства: цепочки равны, если для всех i = 1, . . . , 2n выполняются условия:|l i - k i | ≤ P 1 , |α i - β i | ≤ P 2 , где P₁ и P₂ – пороговые величины.

В описываемой системе пороги устанавливаются пользователем.

УСТОЙЧИВОСТЬ К ВЫБОРУ НАЧАЛА ОБХОДА

Начало обхода при построении цепочек у двух одинаковых скелетов может быть различным. Всего для каждой из них существует 2n циклических сдвигов. Тогда для сравнения двух цепочек достаточно зафиксировать одну из них и сравнить с 2n циклическими сдвигами второй. Если хотя бы одна пара сравниваемых цепочек будет равна, то и исходные цепочки равны между собой, то есть если найдется такое γ = 1, . . . , 2n, что выполняются условия:

|li - kj | ≤ P1, |αi – βj | ≤ P2, i = 1, . . . , 2n,

• i+γ, если i+γ≤2n

где j= 1

• i+γ-2n, если i+γ>2n .

НАХОЖДЕНИЕ ОБЩЕЙ ЧАСТИ У ДВУХ ЦЕПОЧЕК

Рассмотренный алгоритм сравнения двух цепочек требует равенства длин цепочек и, соответственно, совпадения форм фигур, из которых они получены, целиком. Однако на практике зачастую существует необходимость поиска общей одинаковой части у двух фигур. Тогда возникает задача нахождения общей части у двух цепочек.

Рассмотрим простейший скелет и пронумеруем его ребра (рис. 6).

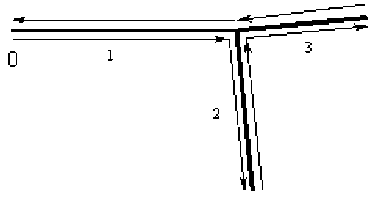
Рис. 6. Простейший скелет

Цепочка, описывающая данный скелет в случае начала обхода в ребре 1, имеет вид:

• {70 ; 95} {50 ; 360} {50 ; 90} {40 ; 360} {40 ; 175} {70 ; 360}.

Пусть необходимо получить цепочку скелета, состоящего только из ребер 1 и 3. Для того этого нужно удалить из строки элементы, соответствующие ребру 2 – l 2 и l 3 , а также угол, связывающий их между собой α 2 . Заметим, что угол между ребрами 1 и 3 (снизу) равняется сумме углов между ребрами 1 и 2 и ребрами 2 и 3, а это углы α 1 и α 3 соответственно. Сложив и объединив эти два угла между собой, получим искомую цепочку: {70 ; 185} {40 ; 360} {40 ; 175} {70 ; 360}.

В общем случае процесс удаления терминального ребра из цепочки можно описать в виде следующих утверждений:

• 1.    Ребро k в цепочке {l i ,α i },i = 1, . . . , 2n является терминальным, если выполняется условие l k = l k+1 и α k = 360.

• 2.    Для того чтобы удалить терминальное ребро k, необходимо из цепочки исключить l k , l k+1 и α k , а α k-1 и α k+1 сложить между собой.

Рассмотренная операция удаления терминального ребра позволяет для цепочки длины 2n получить множество всех подцепочек длины 2r (r ≤ n), описывающих подграфы исходного скелета. Тогда задача поиска общей части длины 2r у цепочек длин 2n и 2m сводится к процессу сравнения всевозможных их подцепочек длины 2r.

АПРОБАЦИЯ АЛГОРИТМА

Описанный метод структурного распознавания бинарных изображений был реализован в виде приложения и протестирован на электронной коллекции изображений петроглифов Северной Фенноскандии [6]. Для тестирования были отобраны 200 черно-белых изображений петроглифов. Результаты работы программы оценивались субъективно автором статьи. Точность работы алгоритма была оценена в 70 % при порогах P1 = 20 и P2 = 30, которые были установлены экспериментальным путем. Для других коллекций изображений, возможно, максимальная точность будет достигнута при других значениях порогов. В табл. 2 представлена информация о средней скорости работы алгоритма для изображения 250 × 250 пикселей (для среднестатистического монитора это приблизительно 8 × 8 см):

Таблица 2

Скорость работы алгоритма

Этап	Время (мcек)
Получение скелета	60
Регуляризация скелета	110
Аппроксимация скелета	1
Получение цепочки	1
Сравнение двух цепочек	6 (для 1000 сравнений)

Как видно из табл. 2, основное время занимают операции получения и регуляризации скелета. Однако для каждой коллекции изображений можно построить цепочки только один раз и в дальнейшем пользоваться ими при поиске. Поэтому в целом можно утверждать, что алгоритм работает достаточно быстро.

ВЫВОДЫ

Рассмотренный способ построения и сравнения структурных описаний скелетов бинарных изображений в виде цепочек примитивов обладает рядом преимуществ:

• 1.    Цепочки устойчивы к повороту фигуры;

• 2.    Цепочка, записанная в обратном порядке, соответствует зеркальному отображению исходной фигуры;

• 3.    Существует возможность сравнивать фигуры как целиком, так и отдельными частями;

• 4.    Выбор ребра – начала обхода скелета не влияет на результат.

Система прошла апробацию на коллекции изображений петроглифов Северной Фенно-скандии [6].

Описанный алгоритм позволяет производить быстрый поиск в электронной коллекции, однако является недостаточно точным. Решением данной проблемы может быть использование двухуров-него поиска – после применения рассмотренного метода поиска, сужающего набор изображений, применяется точный, но медленный метод для окончательного отбора [5]. В дальнейшем планируется усовершенствование алгоритма путем подключения точного алгоритма поиска.