Применение технологий параллельного программирования для систем с общей памятью при решении гиперболических систем уравнений

За последние годы все чаще используются технологии параллельного программирования для решения разного рода задач. Один из классов ресурсоемких задач – это задачи вычислительной геофизики, сейсмики. Задачи такого рода требуют для своего решения большого количества вычислительных ресурсов, поэтому немаловажен вопрос о написании высокопроизводительных алгоритмов для их решения.

С ростом возможностей современных вычислительных систем возникает вопрос об их эффективном использовании. Так как большое количество алгоритмов было написано довольно давно, не все из них могут использовать параллельные системы с достаточной эффективностью и требуют доработки. Так, в работе [1] последовательный код для моделирования эффектов, происходящих в грунте при землетрясении, преобразуется в параллельный. Для этого используются технологии OpenMP и HPF. Авторы сравнивают ускорение и эффективность при выполнении на нескольких процессорах.

• В работе [2] решается задача сейсморазведки. Программная реализация задействует инструкции SIMD. При этом используется несколько ядер для ускорения вычислений с

2.    Математическая модель

помощью технологии OpenMP. В некоторых работах [3] задачи сейсмики решаются с помощью технологий параллельного программирования на системах с распределенной памятью. Авторы [4] рассматривают распараллеливание метода конечных разностей применительно к задачам сейсмики. В работе [5] сравниваются различные технологии написания параллельных программ. Рассматривается решение гиперболических уравнений для моделирования физических процессов.

Иногда при решении такого рода задач возникает дисбаланс между потоками вычислений. Это происходит из-за граничных условий, вычисление которых может требовать большего (или меньшего) количества вычислений, чем вся остальная сетка. Для решения этой задачи может использоваться динамическая балансировка нагрузки. В работе [6] рассматривается такой подход при решении задач распространения сейсмических волн.

Помимо задач сейсмики, техники написания параллельных программ активно применяются для решения задач, где требуется решение других уравнений в частных производных. Например, еще одна работа [7] посвящена совместному использованию OpenMP и векторных инструкций AVX процессора. За счет них авторам удалось добиться ускорения в 57 раз на 10 ядрах по сравнению с одним ядром при решении уравнений мелкой воды и уравнений Эйлера. Авторами другой работы [8] был разработан гибридный метод решения задач гидродинамики с использованием различных технологий распараллеливания как для систем с общей памятью, так и для систем с распределенной памятью.

В NUMA-системах обращение к различным областям памяти может занимать разное время. Работа [9] посвящена этому вопросу. Авторы используют технику, которая заключается в размещении в локальной памяти процесса данных, к которым процесс выполняет наибольшее количество обращений. В результате было получено уменьшения времени выполнения, так как время обращения к локальной памяти быстрее.

В данной работе рассматриваются технологии OpenMP [10] и POSIX Threads. Они предназначены для написания параллельных программ в системах с общей памятью. Это значит, что обмен данными между процессами осуществляется за счет чтения и записи в память, общую для всех процессов. Сравнение этих технологий производилось на задаче решения уравнения линейной динамической теории упругости, которая описывается гиперболической системой уравнений. Эффективность распараллеливания измерялась в отношении времени выполнения последовательной программы к времени выполнения распараллеленной. Для повышения производительности были задействованы векторные инструкции процессора. Они позволяют выполнять несколько арифметических операций над данными за время, требующееся для выполнения только одной операции. Также потокам было запрещено перемещаться между ядрами процессора, чтобы повысить производительность в NUMA-системах.

Для описания поведения среды использовалась модель идеального изотропного линейно-упругого материала. Приведённая ниже система дифференциальных уравнений в частных производных описывает состояние элементарного объёма упругого материала в приближении малых деформаций для двумерного случая:

dv _x _ дс XX . ^дс ху Р dt Эх Әу

д- у _ д« ху . д<Г уу Р dt дх Әу ’

Ә« хх    ,, , _п х dv x , . dv. y Ә« уу _xdv_x             д-у дс у (d- x , Э- у

ПТ _(А .ад^х + х-^У’^ _Х^х + (Х + 2'-> дУ’^Т _Ңах + -у где р — плотность среды; Х, р — параметры Ламе; vx и Vy — горизонтальная и вертикальная составляющие скорости частиц среды; сХХ’ Суу, «Ху — компоненты тензора напряжения.

Данную систему можно переписать в матричной форме:

9гі _{Р    д} du _q        du _q_

~У + АР” д- + ВР« -у _ 0’ где u — вектор из 5 независимых переменных u = (ахх,ауу,сгху,vx,vy)T. Явный вид матриц Ард, Врд представлен в [11]. Здесь и далее подразумевается суммирование по повторяющимся индексам. Собственные значения матриц Ард и Врд таковы: si = —ср, 82 = —cs, 83 = 0, 84 = cs, 85 = ср, где ср и cs — скорости распространения продольных и поперечных волн в среде.

3.    Численный метод

Применяя покоординатное расщепление, можно свести задачу построения разностной схемы для системы уравнений (1) к задаче построения разностной схемы для системы вида

^Р + А рд =0. (2) ot ох

Для гиперболической системы уравнений (2) матрицу A можно представить в виде A = RЛR ^-1 , где Л — диагональная матрица, элементы которой — собственные значения матрицы A , а R — матрица, состоящая из правых собственных векторов матрицы A . Введём новые переменные: w = R ^-1 u (так называемые инварианты Римана). Тогда система уравнений (2) сведётся к системе из 5 независимых скалярных уравнений переноса.

Приведем схему третьего порядка точности для численного решения одномерного линейного уравнения переноса u _t + аи _х = 0, а > 0, и = ат/һ, т — шаг по времени, Һ — шаг по координате:

um+1 = um + ^(△о + △2)/2 + ^(△о — △ )/2 +"—7---"(^1 — 2^0 + ^2),

• △о = <-1 — um,(4)

△ 1 = u”-2 — <-1,(5)

• △2 = u” — u”+1.(6)

4.    Постановка задачи 5.    Измерения

Схема (3) устойчива для чисел Куранта, не превышающих единицу. Используется сеточно-характеристический критерий монотонности, опирающийся на характеристическое свойство точного решения:

”    -»”     -»”+1      я^('ііп”

шш^(и _т —1 ,^u _m⁾ — ^um — шах^(и _т - 1 , ^u _m ).

В местах выполнения данного критерия порядок схемы падает до второго.

После того как значения инвариантов Римана на следующем шаге по времени найдены, востанавливается решение: u ”⁺¹ = Rw ”⁺¹ .

Тестовая модель изображена на рис. 1. Размеры области даны в километрах. На нижней и боковых границах устанавливалось неотражающее граничное условие, на верхней – свободная граница. В качестве источника возмущения использовалась вертикальная сила, приложенная к площадке с 925.7 м по 974.1 м на дневной поверхности, амплитуда которой описывалась импульсом Рикера частоты 40 Гц. Результаты расчета представлены на рис. 2.

Все тесты производились на одной и той же тестовой задаче. При этом использовалась двумерная сетка размерами 4000 х 4000 узлов. Выполнялось 100 шагов по времени. Отдельно были измерены результаты для вычислений с одинарной и с двойной точностью. Каждый узел содержал по 5 переменных, поэтому в случае вычислений с одинарной точностью вся сетка занимала в памяти 305 Мбайт, а в случае двойной точности – 610 Мбайт.

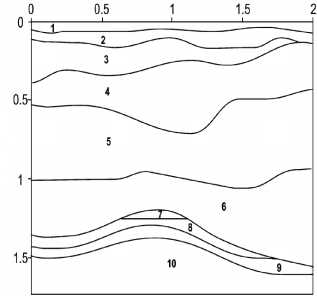
Рис. 1. Геологическая модель антиклинальной ловушки [12]

Рис. 2. Результат расчета – волновая картина в момент времени t = 0 . 38 с

Таблица1

Процессоры, на которых производились измерения

Название (обозначение на графиках)	Частота, ГГц	Кеш, Кбайт	Процессоры и ядра	Компиляторы	Производительность ядра/общая, Гфлопс
AMD Opteron 6272 (a64)	2.1	2048	8 процессоров по 8 ядер	gcc-4.4.6	16.8/1075.2
Intel Xeon E5-2697 (i24)	2.7	30720	2 процессора по 12 ядер	gcc-4.4.7, icc-15.0.0	21.6/518.4
AMD Opteron 8431 (a48)	2.4	512	8 процессоров по 6 ядер	gcc-4.4.7	19.2/921.6

Использовались следующие флаги компиляции: -fno-tree-vectorize, чтобы запретить векторизацию там, где мы ее не хотим использовать, -fopenmp и -pthread для задействования той или иной техологии, -O2 для использования стандартных оптимизаций, -msse, -mavx, чтобы явно указать, какой набор инструкций мы хотим использовать при автовекторизации.

Измерения были произведены на процессорах, указанных в табл. 1. В дальнейшем обозначения используемых компиляторов на графиках – gcc и icc. Обозначения для используемого набора векторных инструкций процессора – sse или avx.

6.    Процесс оптимизации

В первую очередь была написана последовательная версия алгоритма. Пересчет узлов производился в два шага: по оси X (обход сетки в начале по столбцам, потом по строкам) и по оси У (обход сетки в начале по строкам, потом по столбцам). Было измерено количество арифметических операций в коде программы и из этого было получено теоретическое значение флопс – 262, требуемое для пересчета одного узла. На графиках эта версия обозначается simple.

Далее была предпринята попытка оптимизировать шаг по У . На этом шаге был изменен порядок обращения к узлам так, что он совпал с обращением в шаге по X. Таким образом обращение к памяти стало последовательным, что привело к более эффективному использованию кеш-памяти. Кроме того, путем замены арифметических операций на эквивалентные было уменьшено требуемое количество флопс для пересчета узла до 190. Обозначение этой версии на графиках – cache-friendly.

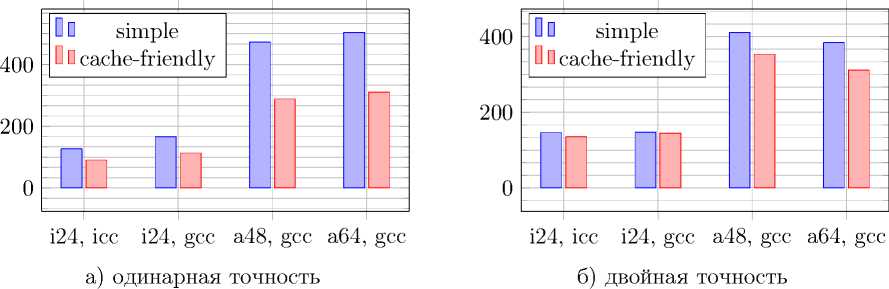
Рис. 3. Время работы в секундах с оптимизацией кеш-памяти и без нее

Время работы первоначальной и оптимизированной версии алгоритма на различных процессорах представлено на рис. 3.

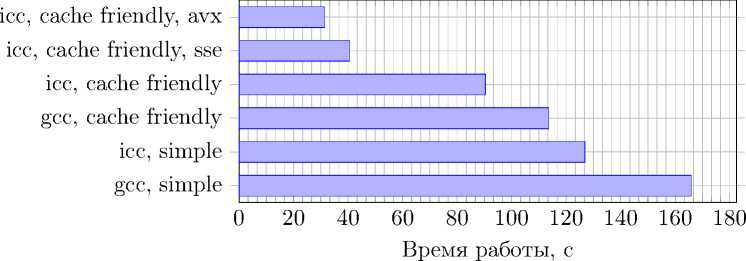
Рис. 4. Время работы при использовании векторизации на Intel Xeon E5-2697, одинарная точность

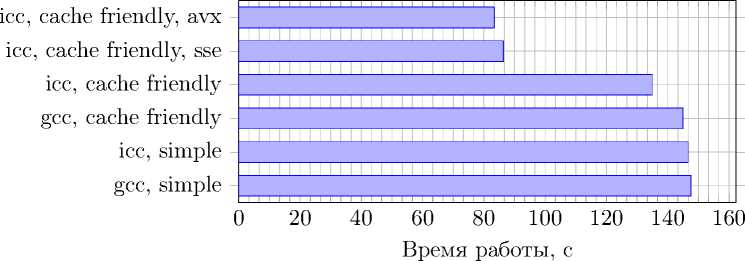
Рис. 5. Время работы при использовании векторизации на Intel Xeon E5-2697, двойная точность

После этого были векторизованы циклы, в которых обрабатывались узлы сетки. Это было сделано с помощью директив (#pragma omp simd) технологии OpenMP, появившихся в стандарте 4.0. Явно было указано, какой набор инструкций должен использоваться: SSE или AVX. Измерения производились только на процессоре Intel Xeon E5-2697. Результаты представлены на рис. 4 и 5.

Исходя из частоты ядра каждого конкретного процессора, была определена его пиковая производительность. Таким образом, был вычислен процент от пиковой производительности для каждого теста (рис. 6, 7).

a48, gcc, cache friendly a48, gcc, simple a64, gcc, cache friendly a64, gcc, simple i24, gcc, cache friendly i24, icc, cache friendly i24, gcc, simple i24, icc, simple i24, icc, cache friendly, sse i24, icc, cache friendly, avx

Рис. 6. Процент от пиковой

a48, gcc, cache friendly a48, gcc, simple a64, gcc, cache friendly a64, gcc, simple i24, gcc, cache friendly i24, icc, cache friendly i24, gcc, simple i24, icc, simple i24, icc, cache friendly, sse i24, icc, cache friendly, avx

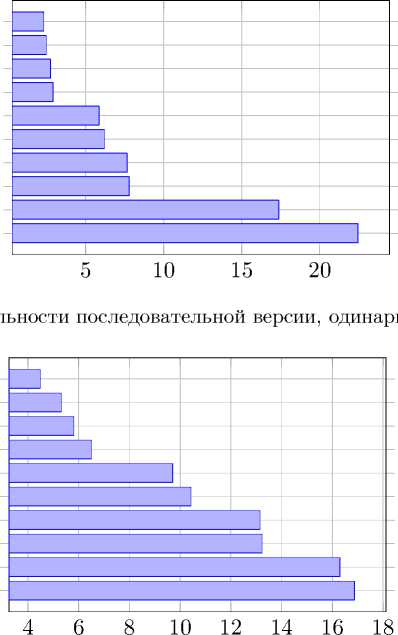
точность

Рис. 7. Процент от пиковой производительности последовательной версии, двойная точность

7.    Параллельная версия

Алгоритм распараллелен с использованием технологий OpenMP и POSIX Threads. При этом отдельно распараллелена каждая из версий, чтобы была возможность пронаблюдать последствия оптимизации последовательного кода на эффективность его распараллеливания.

7.1.    OpenMP

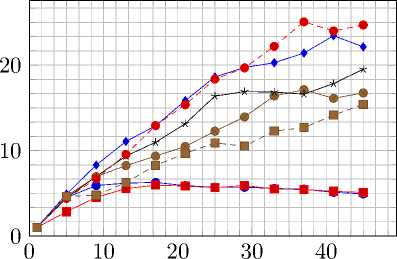
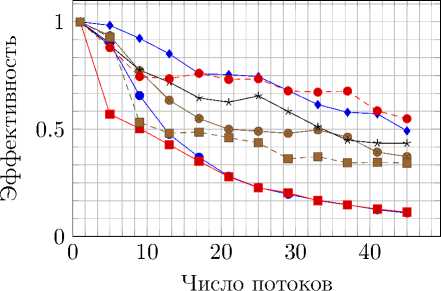
—е— simple,gcc,aff —■   simple,gcc • cf,gcc,aff cf,gcc

—♦— spl-gr,gcc • spl-gr,gcc,aff-е-- pthread,gcc

Рис. 8. Ускорение и эффективность распараллеливания на AMD Opteron 8431 при вычислениях с одинарной точностью

Число потоков

—е— simple,gcc,aff —■— simple,gcc • cf,gcc,aff cf,gcc

—♦— spl-gr,gcc • spl-gr,gcc,aff- гн- pthread,gcc

Рис. 9. Ускорение и эффективность распараллеливания на AMD Opteron 8431 при вычислениях с двойной точностью

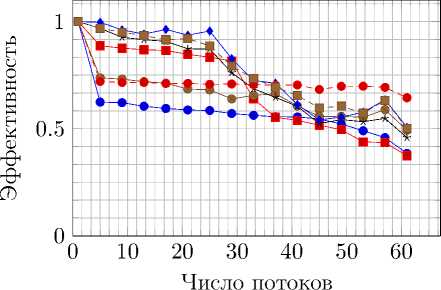
—е— simple,gcc,aff —■— simple,gcc • cf,gcc,aff cf,gcc

—♦— spl-gr,gcc е spl-gr,gcc,aff ■ pthread,gcc с одинарной точностью

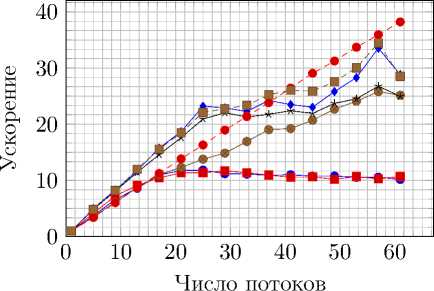
Рис. 10. Ускорение и эффективность распараллеливания на AMD Opteron 6272 при вычислениях

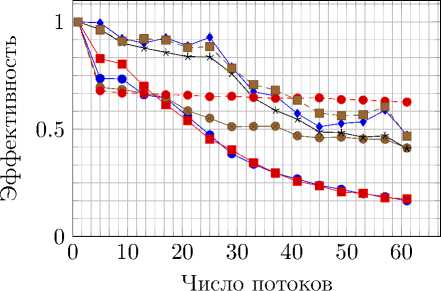
—е— simple,gcc,aff —■— simple,gcc • cf,gcc,aff cf,gcc

—♦— spl-gr,gcc --•-- spl-gr,gcc,aff- -ЕН- pthread,gcc

Рис. 11. Ускорение и эффективность распараллеливания на AMD Opteron 6272 при вычислениях с двойной точностью

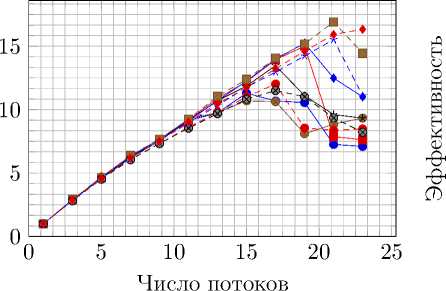
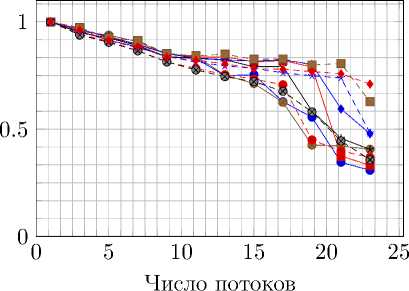
—• simple,gcc —■—  cf,gcc • simple,icc        cf,icc    —♦— spl-gr,icc

• cf,icc,sse -е-- spl-gr,gcc cf,icc,avx spl-gr,icc,avx--♦-- spl-gr,icc,sse

Рис. 12. Ускорение и эффективность распараллеливания на Intel Xeon E5-2697 при вычислениях с двойной точностью без использования привязки потоков к определенным ядрам

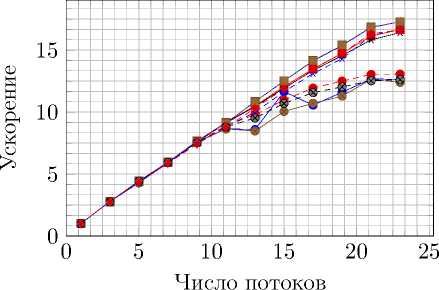
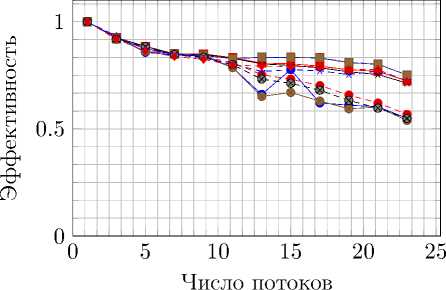
—е— simple,gcc —■   cf,gcc —е— simple,icc        cf,icc    —♦— spl-gr,icc

• cf,icc,sse -е-- spl-gr,gcc cf,icc,avx spl-gr,icc,avx--♦-- spl-gr,icc,sse

Рис. 13. Ускорение и эффективность распараллеливания на Intel Xeon E5-2697 при вычислениях с двойной точностью с использованием привязки потоков к определенным ядрам

Была сделана оптимизация уже параллельного кода. В ней каждый поток выделяет память, необходимую только для пересчета узлов, отданных в распоряжение именно этого потока. Теоретически это должно привести к росту производительности в NUMA-системах, так как память, выделенная конкретным потоком, согласно стандарту OpenMP, выделяется в локальной памяти потока, обращение к которой занимает наименьшее количество времени. Обозначение этой версии на графиках – spl-gr.

Отдельно были произведены измерения, в которых потокам было запрещено перемещаться между ядрами процессора. Это сделано для уменьшения временных затрат. Без этого оптимизация, связанная с разделением сетки на отдельные части для различных процессов, перестает иметь смысл. Обозначение на графиках – aff. Результаты тестов представлены на рис. 8–13.

7.2.    POSIX Threads

Далее OpenMP-версия кода с разделением сетки между потоками была изменена таким образом, чтобы использовать POSIX Threads в качестве технологии распараллеливания (рис. 14).

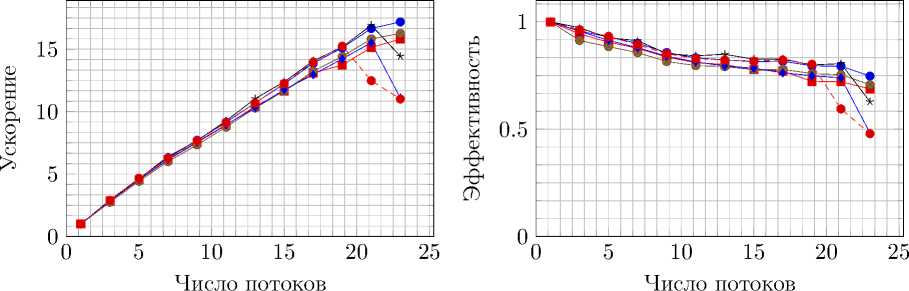
—е— pthread,gcc —■— pthread,icc,avx • pthread,icc spl-gr,gcc —♦— spl-gr,icc,avx • spl-gr,icc

Рис. 14. Сравнение ускорения и эффективности распараллеливания технологий OpenMP и POSIX

Threads на Intel Xeon E5-2697

8.    Заключение

Наибольшая производительность от пиковой для данного процессора была получена в последовательной версии 22% для вычислений с одинарной точностью и 17% для вычислений с двойной точностью с оптимизацией доступа к кеш-памяти и использованием векторных инструкций avx.

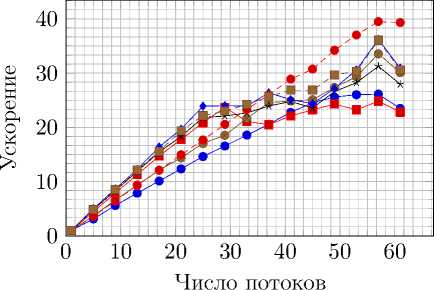
Максимальные полученные ускорения: на AMD Opteron 6272 – в 37 раз на 64 ядрах, на AMD Opteron 8431 – в 25 раз на 48 ядрах и на Intel Xeon E5-2697 – в 17 раз на 24 ядрах.

Таким образом, удалось продемонстрировать, что в системах с общей памятью основным ограничением для ускорения с ростом числа потоков является максимальная скорость взаимодействия с памятью. Разделение памяти между потоками позволяет не обращаться ядрам процессора к нелокальной памяти, а значит, доступ к памяти осуществляется быстрее. Привязка потоков к определенным ядрам уменьшает количество обращений в память, используемых для поддержания когерентности кешей ядер, и также ведет к увеличению производительности. Следует заметить, что реализация параллельной версии с использованием POSIX Threads оказывается сложнее, чем при использовании OpenMP, но при этом не дает значительного прироста производительности или эффективности распараллеливания.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 15-37-20673.