Применение теорем Котельникова в условиях компьютерно-интегрированных технологических систем производства

При отработке методологии технического мониторинга компьютерно-интегрированных технологических систем производства (КИТСП) для механообработки перед автором возникла проблема отсчетов и синхронизации электрических сигналов при циркуляции информации по внешним и внутренним каналам компьютерной управляющей системы (рис. 1.2). [1; 2].

Рис. 1. Функциональная схема управляющей диагностической системы «пресс-штамп-датчик-компьютер» для чистовой вырубки, ее архитектура и аппаратное обеспечение: А1 - блок тензодатчиков; А2 - блок пьезодатчиков;

АЗ - аналого-цифровой преобразователь (АЦП);

А4 - компьютер; А5, Аб, А7 - периферийные устройства (клавиатура, монитор и принтер); ПУ - пульт управления прессом

Работа информационной составляющей КИТСП характеризуется аналоговыми, дискретными и цифровыми сигналами, на которые накладываются наводимые от механики, электрики и электроники технологической системы помехи и шумы (рис. 3), [2; 3].

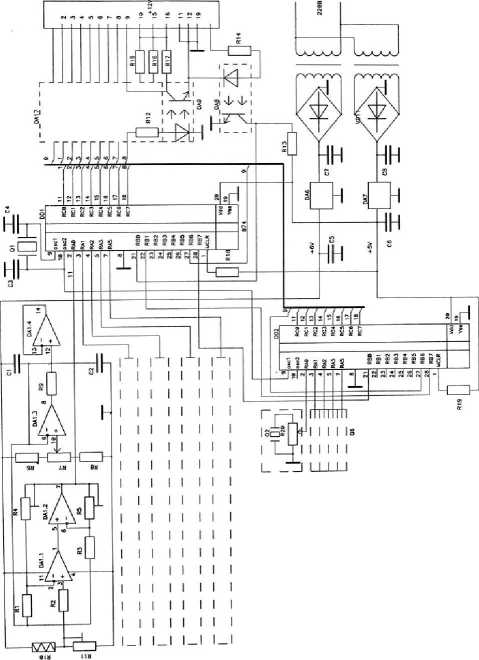
Рис. 2. Принципиальная схема многоканальной управляющей диагностической системы «пресс-штамп-датчик-компьютер» для чистовой вырубки, разработанная автором

Для теоретического решения возникшей проблемы можно использовать семейство теорем В. А. Котельникова, причем теоремы отсчета представляются аналоговым сигналом s^ в виде выражения [4]:

#) -^АСОМО^О.

значения s (/) = 0, а непрерывный спектр 5 (z) представляется в виде ряда (рис. 6) [4]:

где {ф^}, & = 1, 2,... - множество сигналов (функций времени), выбранных заранее независимо от вида s (/); {Т} - множество моментов времени, на котором определены +) и{(рЩ)}, £ = 1,2,_

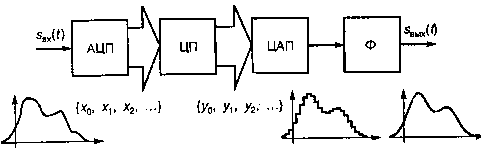
Рис. 3. Обобщенная структурная схема системы цифровой обработки сигналов

sin2jiT /--

Г 2F

2лТ /--

Г 2F

ЕД/w)

= 5+(/Аю)

sin2717(/-/А/) _

2лГ(/-/А/) "

sin[Г(со -/Асо)] Г(©-/Асо)  ’

Основная теорема Котельникова. Справедлива для аналоговых сигналов s^ с ограниченной полосой s (о), когда сигнал s^ задан на бесконечной оси времени, -оо <  t < +оо, когда (VZ е (-oo;oo))(V_T > 0) (рис. 4) [4]:

где Af -шаг отсчета частоты.

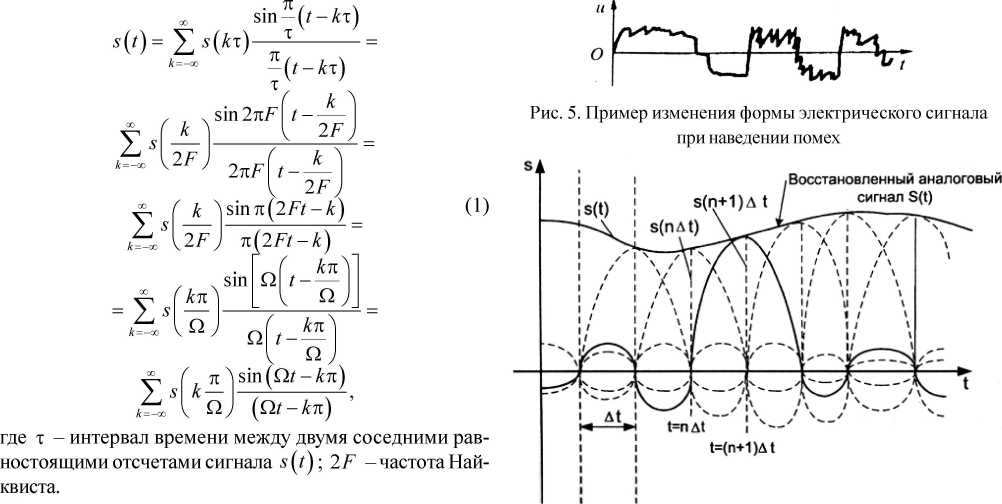
Рис. 6. Графическое представление сигнала s^ согласно основной теореме Котельникова в виде ряда

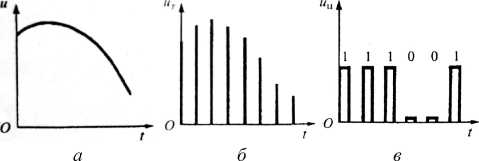
Рис. 4. Характерная форма основных электрических сигналов: а - аналоговый; б - дискретный; в - цифровой

Теорема (2) является теоремой отсчетов в частотной области, когда спектр сигнала s (о) представлен дискретными отсчетами. Теорема (2) дуальна теореме (1).

Теорема 3. Справедлива для сигнала S (/), строго ограниченного на полосе частот Q_o ± tiF, который можно восстановить по формулам [4]:

Теорема 1. Физический смысл которой состоит в том, что она справедлива, когда операции дискретизации, т. е. цифрового преобразования и восстановления сигнала, взаимно обратные, при условии

_ 1 71

2F” Q'

Теорема (1) относится к гипотетической ситуации и характеризует лишь предельные возможности каналов информации, т. е. их пропускную способность (рис. 5).

Теорема 2. Справедлива для сигнала s (/), ограниченного на (/) <  Т и принимающего вне этого интервала

S^ = SS (/) sin Q0Z + SC(z) cos Q^,(3')

где SSQ^, SC (/) - функции, имеющие отличные от нуля спектры АА(со) и АС (со) только для диапазона |о| < tiF, о е [Qo -tiF;Q + tiF],(3")

/х ” sinnFC-Ai)

SS(A = У SSUtA----2

/x ”       sinnFC-Ai)

SC(t\ = У SC(b\ -----2----2, ^{V 7} ^ ^{V 7} uF^t-kx^

(3"')

(3"")

где SS^kx), SC^kx), к=0, ±1, ±2, ...-амплитудные отсчеты, осуществляемые через равностоящие проме-

1 лутки времени с шагом т =    .

Теорема (3')...(3''”) является обобщением основной теоремы Котельникова для случая произвольной полосы частот ширины F.

Теорема 4. Справедлива для функций S^ с конеч-1

ным спектром ±2kF и т < —— согласно интерполяци-1F онной формуле [4]:

ОО ДМ lAtHWN (4)

к=-со 1=0

n";*sin где Ф„ (С т) = —---------------------------.

• 4i )    CL/ •^sin v К -^т™)

Nt             Nt

Функция ф„ (с т) = 1 при t = t_kl , а при t = t_mr (здесь т*к и rd) обращается в нуль, так что s (?_н) равняется правой части (4). Следовательно, ряд (4) равномерно сходится для любого / из ограниченной области.

Таким образом, теорема (4) представляет основную теорему Котельникова для неравномерных отсчетов распределенных по периодически повторяющимся группами из N отсчетов в каждой при выполнении условий:

tkl = Nkx + т7, где к = 0, ±1, ±2,...; 7 = 0,1, 2,..,А-1; т0 =0; т, <.У: 1 т =---

2F '

При каждом фиксированном 7, выборе определенной точки т, внутри группы отсчеты представляют собой последовательность равностоящих значений: ...,f f__lz, t_(ll^t_Yl^t_2l^....

Теорема 5. Справедлива для сигнала S' (?) с ограниченным спектром |со| < 2 л/*' = — [4]:

к —1        j^

где ф(0= п sin3-0-z/).

,=~” кт

В теореме (5) последовательность DL моментов отсчетов удовлетворяет условиям:

• 1)    t_k+x -t_k > с > 0 для всех к = 0, ± 1, ± 2,...;

• 2)    среднее значение интервала между отсчетами

(4 к_к)

■” 2к

Теорема (5) является обобщением теоремы (4) для неравномерных отсчетов, на которые наложены достаточно общие необременительные условия. К тому же если отсчеты разбросаны по оси времени достаточно регулярно и не образуют скоплений и сгущений, то теорема (5) становится весьма полезной при дискретизации аналоговых сигналов в каналах информации.

Теорема 6. Справедлива для сигнала S (?), если спектр §Q^ сигнала S(?) ограничен полосой |/|-^ и характерная средняя длительность интервала между отсчета-1

ми составляет т < —, где при достаточно малых 2F т —> 0 получается предельное равенство [4]:

= ^ [£(2Ь) + (7-2.Кт)£'(2Ь)] к=-ад

Таким образом, хотя версии основной теоремы Котельникова (1) уже были известны в работах Найквиста, Уиттеккера, Ватсона, Гончарова и др., но лишь В. А. Котельников смог увидеть в ней физический смысл и указал ее инженерное применение в современных условиях цифровых систем, включая КИТСП, с точки зрения теории сигналов и теории информации. Теорема (1) и ее версии (2)...(6) определяют условия, при которых аналоговый сигнал s(?) точно восстанавливается по дискретным отсчетам, заданных на конечных подмножествах временной оси t с требуемой точностью при наличии стационарных случайных помех. Они позволяют обеспечить большую информационную емкость каналов, а также организовать многоканальный режим их работы с временным делением каналов.

С математической точки зрения, основная теорема Котельникова и ее версии считаются частным случаем теоремы интерполяции в теории целых функций.