Применение теории катастроф к анализу технологических систем

Большинство исследований в трикотажной отрасли посвящено системам, возможные изменения состояния которых рассматриваются как непрерывные. Кажется вполне естественным, что непрерывные изменения входных воздействий X 1 , X 2 ,..., X k должно вызывать непрерывное изменение реакции системы Y. Но, так бывает не всегда. Это обусловлено тем, что непрерывность изменений состояния системы связана с ее устойчивостью: при потере системой устойчивости, непрерывным изменениям X 1 , X 2 ,..., X k могут соответствовать скачкообразные изменения реакции Y [1].

Один из выдающихся математиков ХХ-го века Том Р. разработал глубокую теорию скачкообразных изменений, названных им катастрофами [2]. С точки зрения физики или техники, катастрофа – это скачкообразное изменение реакции системы Y при плавном, непрерывном изменении параметров состояния X i . В этой теории поведение системы описывается переменными X 1 , X 2 ,..., X k , рассматривающимися как внутренние или переменные состояния. Переменные q 1 , q 2 ..,q k составляют группу внешних переменных и вводятся в качестве переменных управления. Поведение системы задается потенциалом V. В общем случае V=V(X 1 , X 2 ,..., X k ,..., q 1 , q 2 ..,q k ). Состояниям равновесия системы соответствуют стационарные (независящие от времени) значения потенциала. В них первые производные от потенциала по переменным состояния обращаются в ноль.

Один из важнейших методов теории катастроф связан с применением ряда Тейлора. Применение его позволяет изучение свойств n-ое число раз дифференцируемой функции свести к более простой задаче изучения свойств соответствующего многочлена, каким является приближающая ее определенная часть ряда Тейлора. Общая схема процедуры анализа систем на устойчивость в рамках теории катастроф состоит в следующем.

На первом этапе по отношению к системе выбираются две группы величин. Из них первая содержит переменные состояния системы, вторая – переменные управления. На следующем этапе вводится функция, для которой эти переменные являются ее аргументами. Изучение устойчивости системы в большинстве случаев сводится к выявлению особенностей связи переменных состояния с переменными управления. Поэтому на третьем этапе исследования, факт обращения в ноль первых производных от потенциала по переменным состояния в точках экстремумов и перегибов используется для построения уравнений связи между переменными состояния и переменными управления или уравнений равновесия. Решениями этих уравнений оказываются траектории или поверхности равновесия в пространстве переменных состояния и управления. Устойчивость равновесных состояний может быть оценена по вторым производным от потенциала по переменным состояния.

Применение теории катастроф к анализу конкретной системы становится возможным, если удается отыскать величину, которую можно принять в качестве потенциала и построить функцию, описывающую зависимость ее от переменных, принимаемых в качестве переменных состояния и переменных управления. Исследования с применением теории катастроф в других областях показывают, что в такими величинами чаще всего оказываются величины энергетического типа, к которым, в частности, относятся показатели интенсивности функционирования системы. Примем во внимание это соображение и будем использовать его как принципиальную рекомендацию.

С наиболее общих позиций технологическую систему в трикотажном производстве можно описать минимум тремя независимыми переменными X, Y, g. Здесь X – численность работающего оборудования; Y – численность работниц, занятых производительным трудом; g – теоретическая производительность оборудования. Введем теперь некоторую функцию:

F = f (X, Y, g) (2)

и попытаемся сконструировать конкретную форму, в которой ее можно использовать в качестве потенциала технологической системы. Условимся, что f (X, Y, g) дифференцируема k раз. В теории катастроф функция, описывающая потенциал системы, представляется в виде разложения в ряд по степеням тех ее аргументов, которые рассматриваются в качестве переменных состояния системы. По отношению к функции (2) естественным в технологическом плане представляется выбор из трех ее аргументов в качестве переменной состояния величины g. Остальные два аргумента X и Y целесообразно рассматривать как переменные управления. Тогда (2) можно записать в форме разложения в ряд по степеням разности (g-g 0 ) в окрестности точки g 0 :

F=F 0 +A(X,Y, g 0 )(g-g 0 )+B(X,Y, g 0 )(g-g 0 )² + С(X,Y, g 0 )(g-g 0 )³ +... (3)

Если коэффициенты данного разложения A, B, C,..., являющиеся функциями переменных X и Y в точке g0, определять по формуле (1), отыскивая частные производные последовательно возрастающих порядков от F по g, то (3) окажется разложением в ряд Тейлора, чаще всего используемого в теории катастроф. В форме (3) технологический смысл функции f(X,Y, g) начинает проступать сразу. Действительно, выделим линейную часть ряда (3), обозначив ее через Fл. При g0=0 Fл=A(X,Y)g. И аналогия данного выражения с соотношением, определяющим норму производительности единицы технологического оборудования Hм = КПВ·g, где КПВ – коэффициент полезного времени, очевидна. Эта аналогия указывает на возможность трактовки функции F через производительность технологической системы. Конкретизируем ее вид применительно к технологической системе – цеху, например, в производстве чулочно-носочных изделий.

Используем методику расчета показателей и параметров технологической системы в названной области, известную из [3]. Введем величины:

Т – общее время работы оборудования (в частности, рабочая смена);

Т м – машинное время вязания единицы продукции;

Т б – затраты времени на подготовительно-заключительные операции;

Т вн – время, необходимое для проведения вспомогательных технологических операций, производимых во время останова машины;

Т ср – потери времени из-за срывов изделий;

Н м – норма производительности единицы оборудования;

Н о – норма обслуживания работницы;

Н в – норма выработки работницы (за время работы);

X – численность работающего оборудования;

Y – число работниц, обслуживающих X единиц оборудования;

К а – коэффициент, учитывающий удельный вес машинного и вспомогательного времени в общем времени работы Т;

К с – коэффициент, учитывающий потери времени из-за совпадений остановов машин рабочей зоны при обслуживании ее одной работницей.

Опираясь на методику [3], легко показать, что:

H=(Т – Т б )/(T/g+T вн + T ср )/(T/g+T ср (X/Y – 1)(1 – K а ))(T/g)X       (4)

Соотношение (4) определяет сменную выработку цеха, содержащего X единиц работающего оборудования с производительностью g и Y работниц. Величину Н назовем производительностью системы.

Проведем несложные преобразования соотношения (4), выделив в знаменателе квадратичную форму относительно g:

H=A 1 A 2 XYg / [A 2 ² Y+(A 2 A 4 X+(A 2 A 3 – A 2 A 4 )Y)g+A 3 A 4 (X – Y)g²],      (5)

где A 1 =T - T б ; A 2 =T; A 3 =T вн + T ср ; A 4 =T вн (1- K а ). В итоге получаем выражение для Н как функции трех переменных: Н = Н(X,Y, g).

Таким образом, функция типа (2), т.е. функция переменных X,Y, g, описывающая технологические системы по меньшей мере в круглочулочном производстве, существует.

Поверхность, описываемая функцией Н = Н(X, g) при Y=Const изображена на рис. 1а и в повернутом положении – на рис. 1б. Сложная форма ее содержит особенность, состоящую в том, что в определенной ее области одно и то же значение Н достигается при различных значениях X. Например, значение H=14000 изд./смену достигается при двух совершенно разных уровнях производительности технологического оборудования: при g=150 и g=1000. При малом числе работниц Y, занятых производительным трудом и фиксированном значении X, такой эффект обязательно возникает. Вначале рост производительности g технологического оборудования повышает производительность системы, т.к., несмотря на невысокую численность работниц, рост их загруженности и снижение коэффициента потерь времени из-за совпадений нейтрализуется ростом производительности машин. В дальнейшем производительность системы, достигнув максимума, начинает неуклонно снижаться. Это объясняется эффектом быстрого снижением значения коэффициента К с , определяющего потери времени в работе машин, обслуживаемых одной работницей из-за совпадений остановок двух и более машин одновременно.

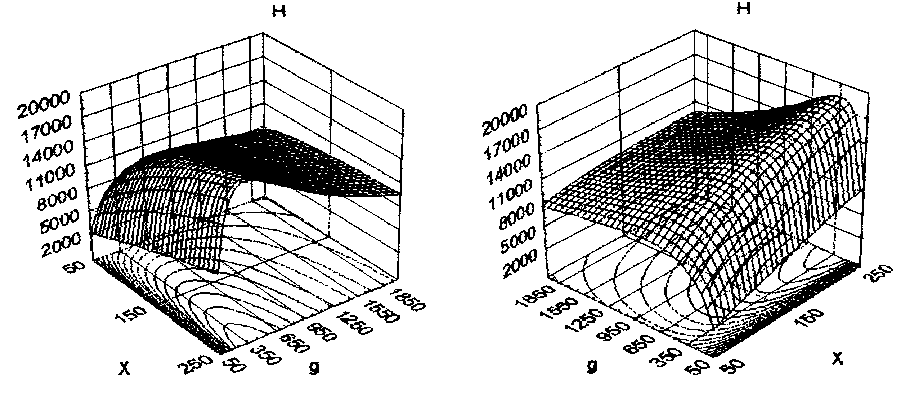
а)                                                б)

Рисунок 1 – Вид поверхности значений функции H=H(X, g) при Y=5

Технологические характеристики для расчета параметров функции (5): T=29520 с., T б =1800 с., T вн =16 с., T ср =31 с., K а =0,8.

Выясним теперь, какие состояния технологической системы являются равновесными. Выше было отмечено, что равновесное состояние системы достигается в тех точках, в которых первая производная от потенциала по переменной состояния оказывается равной нулю. Используем это определение для поиска состояний равновесия системы. Отыщем первую производную от потенциала системы в по переменной состояния g. Преобразуем (5), применив такую замену переменных: H=F; A 1 A 2 XY=q 0 ; A 2 ²Y=q 1 ; A 1 A 4 X+(A 2 A 3 –A 2 A 4 )Y=q 2 ; A 3 A 4 (X–Y)=q 3 . Тогда выражение для потенциала системы примет вид:

F=q0g/(q1 + q2+ q3g2)(6)

После дифференцирования по переменной g получим:

∂F/∂g = (q0q1 – q0q3 g2)/( q1+ q2g + q3g2) 2(7)

Из последнего выражения следует, что ∂F/∂g = 0 при g = (q 1 /q 3 )^0.5. Возвращаясь к более удобным для последующего анализа величинам X и Y, имеем:

g = (bY/(X–Y))0,5,(8)

где b=A 2 ²/(A 3 A 4 ). На рис. 2 представлено геометрическое отображение функции (8) в пространстве параметров X,Y, g при реальных диапазонах возможных значений переменных управления X и Y. На этом рисунке видно, что фазовые точки, соответствующие состояниям равновесия рассматриваемой системы, образуют в фазовом пространстве X,Y, g поверхность. Следовательно, система обладает большой свободой совершать движения по поверхности равновесия в пространстве переменных X,Y, g. Это означает, что равновесные ее состояния достижимы при многих сочетаниях уровней переменной состояния g и переменных управления X, Y.

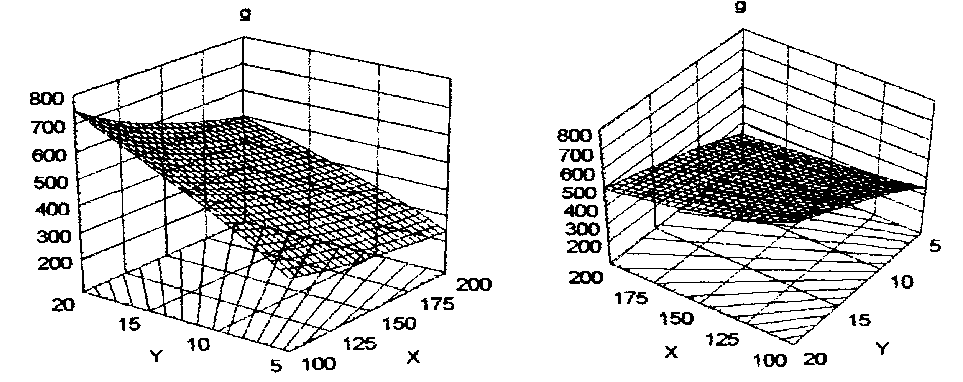
а)                                                                      б)

Рисунок 2 – Поверхность равновесия технологической системы, описываемая функцией (8) в фазовом пространстве XYg

Значения характеристик технологической системы приведены под рис. 1.

Однако равновесным состояние системы будет до тех пор, пока отображающая его фазовая точка будет оставаться на поверхности равновесия. Переход системы в неравновесное состояние интерпретируется как отрыв фазовой точки от этой поверхности. Интегральной ее характеристикой является максимум производительности системы в каждой ее точке, что отличает эту поверхность от всех других в этом пространстве.

Поставим теперь вопрос об устойчивости состояния равновесия. Известен ряд критериев устойчивости. Одним из наиболее простых, но позволяющих однозначным образом решить данный вопрос, является критерий знака первой производной от потенциала системы по переменной состояния. Применительно к рассматриваемой системе он будет состоять в следующем: если при переходе через точку равновесия функция в правой части (6) меняет знак с плюса на минус, то состояние равновесия устойчиво. Во всех остальных случаях оно неустойчиво. Чтобы применить этот критерий, перепишем выражение (7) в виде разности двух дробей:

∂F/∂g = (q 0 q 1 - q 0 q 3 g²)/(q 1 + q 2 g + q 3 g²) ²= (q 1 /q 0 )/g²[q 0 g)/ (q 1 + q 2 g + q 3 g²) ²] –

– (q 1 /q 0 )[q 0 g)/ (q 1 + q 2 g + q 3 g²) ²].

Учитывая соотношения (6) и (8), получаем:

∂F/∂g = F²/q 0 [q 1 /(kg)² - q 3 ]                                  (9)

где k – некоторый безразмерный коэффициент. При k=1 и значении g, определяемом соотношением (6), dF/dg = 0, и фазовые точки в пространстве gXY лежат на поверхности равновесия (рис. 2). При значениях g, меньших определяемых (8), фазовые точки будут лежать ниже поверхности равновесия, при больших – выше этой поверхности. Проследим за знаком правой части (9) по мере прохождения фазовой точки через поверхность равновесия. Из (9) следует, что знак этой части определяется знаком разности в прямых скобках. При k<1 kg1. После такого перехода имеем kg>g, что приводит к изменению знака правой части (9) на отрицательный. По принятому критерию заключаем, что состояния равновесия на поверхности (8) устойчивы.

Для подтверждения полученного вывода оценим знак второй производной при g =(q 1 /q 3 )^0.5. Получим ее, дифференцируя (7):

∂²F/∂g² = 2(q 0 q 3 ²g³-3q 0 q 1 q 3 g-q 0 q 1 q 2 )/(q 1 + q 2 g + q 3 g²) ²                 (10)

Знак этой производной определяется знаком числителя. После подстановки в числитель значения g =(q 1 /q 3 )^0.5 и сокращения на q 0 q 1 получим:

- 2(q 1 /q 3 )^0.5 - q 2 < 0

Введенные выше соотношения показывают, что величины q 1 ,q 2 , q 3 могут быть только положительными. Следовательно, фазовые точки на поверхности (8) соответствуют состояниям устойчивого равновесия технологической системы.

Подводя итог анализу рассмотренной технологической системы, отметим, что в пространстве параметров X,Y, g существует поверхность, образованная такими их значениями, при которых состояние этой системы равновесно и устойчиво. При других их значениях состояние системы неустойчиво. Это объясняет факт неуклонного стремления технологической системы в направлении падения ее производительности, который наблюдается на практике в условиях, когда управляющие воздействия отсутствуют или недостаточно интенсивны. Как следует из полученных результатов, приблизить технологическую систему к состоянию устойчивого равновесия можно путем использования высокопроизводительного оборудования. Этот вывод делает понятной и оправданной мировую тенденцию роста производительности вязального оборудования для трикотажного производства, в частности, круглочулочных автоматов.