Применение теории конечных автоматов при моделировании сложных систем с использованием программы Stateflow

В ходе проектирования сложных реактивных систем, возникает проблема реализации программной части для описания их алгоритма поведения. Такие программы отличаются большой громоздкостью, по ним сложно проследить всю логику работы, кроме того на данный момент нет четкой структуры, которую можно было бы применить для нескольких систем.

В 1991 г. А.А. Шалыто было предложено решение данной проблемы: Switch-технологии - технология разработки систем логического управления на базе конечных автоматов, охватывающая процесс спецификации, проектирования, реализации, отладки, верификации, документирования и сопровождения была предложена.

В данной технологии автоматы применяются не как одну из моделей дискретной математики, а как универсальный подход, который целесообразно использовать практически всегда, когда программа должна обладать достаточно сложным поведением. Данный подход соединяет разработку приложений с методами построения управляющих систем.

Автоматное программирование используется для проектирования реактивных систем управлений, взаимодействующих с окружающей средой путем обмена сообщениями в темпе, задаваемом средой. К этому классу можно отнести большинство телекоммуникационных систем, а также системы контроля и управления физическими устройствами.

Рассмотрим подробнее управляющие автоматы, которые используются при построении модели автоматизированного объекта управления. Предпосылкой для создания такого типа автоматов была необходимость проектирования и реализации систем со сложным поведением.

Автомат, в данном случае, не только имеет конечное число состояний, но, кроме того, реализуемые им функции переходов и выходов оперируют исключительно конечными множествами. Именно это свойство позволяет описывать логику поведения машины явно: в виде таблицы или графа переходов. Поэтому свойство конечности устройства управления необходимо сохранить при построении модели автоматизированного объекта. Более того, это свойство целесообразно усилить следующим неформальным требованием: число управляющих состояний, входных и выходных воздействий должно быть небольшим.

При рассмотрении всевозможных деталей использования автоматных моделей в программировании становится ясно, что выбрать одну конкретную модель, подходящую для всех задач, невозможно. При программной реализации сущностей со сложным поведением применение могут найти активные и пассивные, разомкнутые и замкнутые модели, различные формы представления и интерпретации входных и выходных воздействий. Модель автоматизированного объекта управления должна быть применима для любой сущности со сложным поведением, и поэтому целесообразно сформулировать ее довольно абстрактно.

Приведем формальное определение автоматизированного объекта управления.

Пара A,O , состоящая из управляющего автомата и объекта управления, называется автоматизированным объектом управления.

Управляющий автомат представляет собой шестерку (X, Y, Z, y , δ, φ ), где:

X X X – конечное множество входных воздействий, причем каждое входное воздействие x состоит из компоненты x , порождаемой внешней средой, и компоненты x , порождаемой объектом управления;

Y – конечное множество управляющих состояний;

Z – конечное множество выходных воздействий;

y Y – начальное состояние;

• •    ф=(ф»чн – функция выходов (выходных воздействий), состоящая, в общем случае, из двух компонент: функции выходных воздействий в состояниях qY Y ^Z и функции выходных воздействий на переходах Ф" : XxY^Z ;

• •  5 : XxY ^Y - функция переходов.

Объект управления – это тройка (V, f_q , fc ), где:

V – потенциально бесконечное множество вычислительных состояний (или значений),

• •  f_q : V^X о   – функция, сопоставляющая входное воздействие

вычислительному состоянию,

• •  f_c : ZxV ^>V - функция, изменяющая вычислительное состояние в

зависимости от выходного воздействия.

Функции f и f являются математическими эквивалентами набора запросов и набора команд соответственно.

Графическое представление описанной модели приведено на рис. 1.

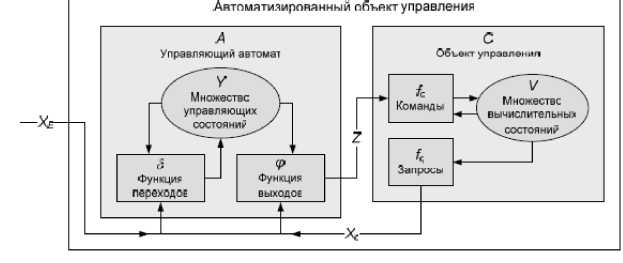
Рис. 1.

Основные этапы проектирования системы:

• •    Исходными данными задачи считается не только словесное описание целевого поведения системы, но и (более или менее) точная спецификация набора событий, поступающих в систему из внешней среды, и множеств запросов и команд всех объектов управления.

• •    Строится набор управляющих состояний.

• •    Каждому запросу объектов управления ставится в соответствие входная переменная автомата, каждой команде – выходная. На основе управляющих состояний, событий, входных и выходных переменных строится автомат, обеспечивающий заданное поведение системы.

• •    Построение визуального интерфейса системы:   «Система

управления» - «Оператор».

В качестве примера рассматривается модель «Частотнорегулируемый привод – Задвижка».

Введем обозначения входов и выходов, которые затем будут использоваться в моделировании:

• 1.    Входные (управляющие) воздействия:

• 2.    Выходные данные:

х1 – «Открыть», х2 – «Закрыть».

z1  – «Задвижка открыта», z2 – «Задвижка закрыта», z3  –

«Переходное состояние».

Для моделирования системы используется программа MatLab с подпрограммным пакетом Simulink, а так же графическое приложение Stateflow.

Модель системы в программе Similink (рис. 2):

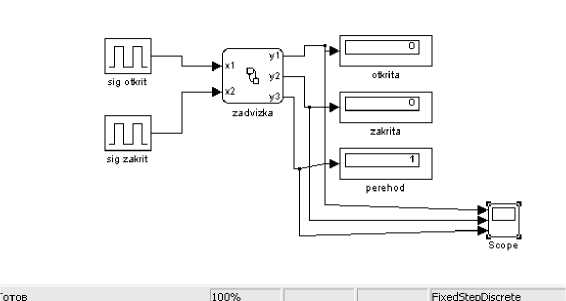
Рис. 2.

Блок “zadvizka” на диаграмме – элемент программы StateFlow, при помощи которой реализован конечный автомат управления задвижкой с 2-мя управляющими сигналами и переходным состоянием (рис. 3):

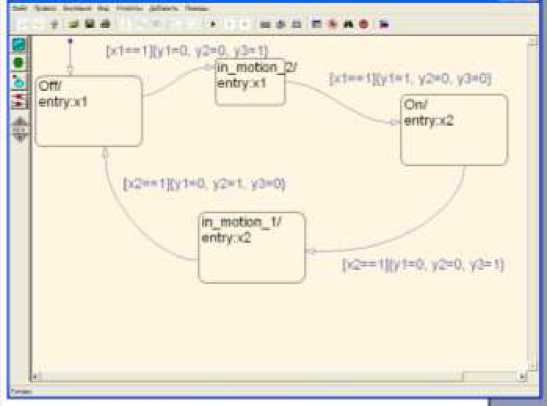
Рис. 3.

Итоговый график переходных процессов представлен на рис. 4.

Рис. 4.

Выводы

Автоматный подход обеспечивает создание управляющего автомата в строго соответствии с техническим заданием, точное документирование разработки, существенно облегчает отладку и сопровождение проекта.

Использование конечного автомата при реализации визуальной части проекта упрощает моделирование сложных систем, не требует вычисления математических моделей. Сложность данного подхода состоит только в корректной передаче значений автомата и реализации выходных воздействий из автомата.