Применение теории нечетких множеств к построению моделей риска электроустановок

Анализ сложных человеко-машинных систем показывает, что ее компоненты, в частности «человек», «электроустановка» и «внешняя среда», функционируют в условиях объективной неопределенности, из чего возникает необходимость многокритериальной оценки таких систем [1]. С одной стороны, система безопасности электроустановок (СБЭ) должна обеспечивать по возможности наибольший уровень безопасности (или наименьший уровень техногенного риска), а с другой ‒ необходимо при этом стремиться к минимизации различного рода ресурсов (материальных, финансовых, трудовых). Поэтому очевидной представляется многокритериальная постановка задачи оптимизации СБЭ. Эти критерии можно условно разделить на технические, экономические и социальные.

В качестве технических критериев могут быть использованы вероятностные характеристики уровня безопасности, математическое ожидание числа электропоражений, максимальное значение вероятности электробезопасности или минимальное значение вероятности электропоражения, надежность (безотказность) работы оптимальной СБЭ. Также к техническим критериям можно отнести математическое ожидание числа предотвращенных случаев электротравм или пожаров [2]. К экономическим критериям можно отнести капитальные вложения в СБЭ, величину предотвращенного ущерба, затраты на обслуживание СБЭ и т.д. В качестве социальных критериев можно принять ухудшение условий жизни, людские потери от пожаров и электропоражений, ущерб окружающей среде от техногенных катастроф и т.д. Как правило, эти критерии взаимосвязаны. Так, надежность, являясь техническим показателем, влияет на экономический: повышение надежности СБЭ может привести к увеличению затрат на ее создание, а снижение затрат ухудшает уровень надежности, что, в свою очередь, приводит к увеличению ущербов.

Многокритериальная постановка задачи оптимизации СБЭ приводит к необходимости нормирования частных критериев, к единому масштабу, так как природа этих критериев различна, что затрудняет операции с ними. Нормирование ‒ это, по существу, выражение численных значений всех частных критериев в относительных единицах и в одном масштабе (как правило, от 0 до 1).

Существует две формы свертки частных критериев ‒ аддитивная и мультипликативная.

Согласно аддитивной форме свертки оценочный функционал F определяется как:

F A =T. V=i frA i ,                                    (1)

где f - нормированный i -й частный критерий; A i - весовой коэффициент, оценивающий значимость i -го критерия.

Мультипликативный способ свертки частных критериев позволяет определить оценочный функционал:

F_M = О)^                   (2)

где « - показатель значимости i -го частного критерия. Если оценочный функционал должен стремиться к минимуму, а частный критерий к максимуму или наоборот, то значение этого критерия необходимо брать в степени (-1).

Мультипликативная форма свертки более предпочтительна, так как выбор оптимального решения не зависит от способа нормирования и числа рассматриваемых вариантов. Исключение составляют случаи, когда частные критерии принимают значение ноль, тогда следует переходить к аддитивной форме свертки, используя естественное нормирование или нормирование по Сэвиджу [3].

Многокритериальный подход к оптимизации СБЭ приводит к рассмотрению явлений (процессов) недетерминированного (неопределенного, нечеткого) характера. Отметим, что информация в соответствии с теорией принятия решения [4] подразделяется на детермирован-ную, стохастическую и неопределенную:

• ‒    детермированными являются те факторы, которые имеют фиксированные заданные значения (физические константы, технические характеристики и т.д.), физические процессы описываются дифференциальными уравнениями с частными производными;

• ‒    стохастические факторы обладают случайной природой с известными законами распределения;

• ‒    неопределенные факторы задаются лишь областью, внутри которой они могут находиться, учитываются в сложных человеко-машинных системах. К неопределенным факторам можно отнести также риски опасности электропоражений или возникновения пожаров, величину ущербов и потерь. В качестве неопределенных могут рассматриваться факторы, получение информации о которых возможно ценой затрат заведомо больших, чем эффект от ожидаемого результата решения. В этих случаях возникает задача принятия решений в условиях неопределенности «природы» или «среды». В многокритериальных задачах с неопределенными величинами для принятия решений требуется из множества известных математических методов выбрать наиболее эффективные и дающие наилучшее решение. К таким методам следует отнести экспертные системы и нечеткую логику.

Остановимся на этих вопросах более подробно.

Сбор и обработка данных, характеризующих техническое состояние электроустановок, сопряжены с анализом значительных объемов информации. Для решения задач моделирования, как уже отмечалось, применяются детерминистические и вероятностные методы. Однако при рассмотрении задач в области теории принятия решения, где рассматриваются многокритериальные модели и конфликтная внешняя среда, приходится сталкиваться с неопределенностью. Эта неопределенность вызвана либо неоднозначностью исходных данных, либо разнородностью и нечеткостью, где наряду с количественными оценками параметров присутствуют качественные – лингвистические ‒ виды («хорошее – плохое»). Здесь «не работают» вероятностно-статистические или другие аналитические методы, поэтому возникает проблема снятия этой неопределенности. Преодолеть эту проблему позволяет использование эвристических подходов, в частности экспертных систем и нечеткой логики (НЛ). Аппарат НЛ представляет собой алгоритм построения многоуровневого автоматического классификатора, позволяющего на основе имеющегося множества разнородных рискообразующих факторов компонентов человеко-машинной системы построить инфологическую кластерную модель с использованием символьного, а не числового способа представления знаний*.

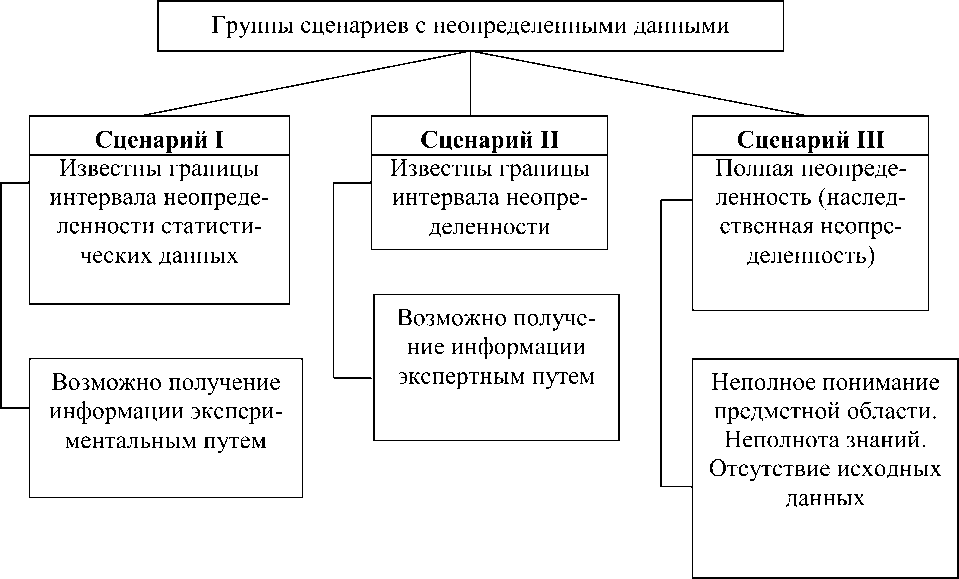
Рис. Сценарии неопределенностей системы (Ч ‒ ЭУ ‒ С)

В качестве методов обработки информации применяется процедура логического вывода и эвристического поиска принятия решения.

Применение аппарата НЛ представляется перспективным, поскольку не требуется априорного знания статистических распределений и их числовых параметров, вместе с тем позволяет оценить техническое состояние объекта (электроустановки (ЭУ)) с использованием определенного набора признаков и соответствующей базы знаний и отнести его к некоторому классу состояний вида (допустимое, опасное, критическое). Рассмотренный подход позволяет не только определить интегральный риск ЭУ и его составляющие, но и прогнозировать его значение путем оценки остаточного ресурса ЭУ. Это, в свою очередь, дает возможность принять соответствующие меры по предотвращению отказов, аварии, пожара. Необходимость определения остаточного ресурса ЭУ, как правило, возникает для прогнозирования срока службы за пределами нормативного значения с целью вывода в ремонт или демонтажа при возникновении риска опасности дальнейшей эксплуатации.

Будем полагать, что точечная оценка является предельным случаем интервальной. Выбор метода оптимизации в условиях неопределенности исходных данных, как уже отмечалось, зависит от полноты и характера информации. Ниже приведен перечень возможных сценариев, каждому из которых соответствует свой уровень неопределенности при анализе человеко-машинных систем (Ч – ЭУ – С).

Первый сценарий реализуется с помощью вероятностно-статистических методов, предполагая сбор и анализ исходных данных.

Второй ‒ предполагает получение информации экспертным путем с использованием теории нечетных множеств.

Третий ‒ реализуется с помощью критерия Байеса по предварительно полученным точечным значениям вероятностей состояния компонентов рассматриваемой системы.

Критерий Байеса предполагает выбор решения по минимуму математического ожидания оценочного функционала:

В(р, Фк) = тт^В^р, фк) = тт^Ф [^=1 Pj • fjk],             (3)

где ф к - оптимальная стратегия; р - распределение вероятностей среды, причем 2 =1 P j = 1; B(p, ф к ) - математическое ожидание оценочного функционала решения.

Байесовские сети доверия [5] применяются при моделировании сценариев, содержащих полную неопределенность (или причинно-следственную сеть). Другими словами, любые события можно объяснить причинно-следственными связями. Соединение методом причин и следствий с помощью вербальных средств позволяет проще оценить (на качественном уровне) вероятности событий.

Рассмотрим основные положения теории нечетких множеств, используемой для анализа сценария II, когда информация о компонентах человеко-машинной системы носит нечеткий характер и может быть представлена функцией принадлежности [6].

Обработка данных о техническом состоянии электроустановок связана со статистическим анализом значительного массива данных о рискообразующих факторах человеко-машинной системы. Причем эти факторы могут иметь качественный и количественный характер. Поэтому перспективно применение метода кластеризации, не требующего априорного знания законов распределения, на базе теории нечетких множеств и аппарата лингвистической переменной. Нечеткое множество представляет класс ЭУ, в котором отсутствует резкая граница между теми ЭУ, которые входят в этот класс, и теми, которые в него не входят.

Сформулируем более точное определение. Пусть Q = (q) - совокупность ЭУ. Тогда нечеткое множество D в Q есть совокупность упорядоченных пар D = (q, p n (q), q £ Q), где p D (q) представляет собой степень принадлежности q к D, u d : Q >M - функция, отражающая Q в пространстве М , называемое пространством принадлежности. Когда М содержит только две точки 0 и 1, D является четким и его функция принадлежности совпадает с характеристической функцией обычного множества [6]. Далее будем полагать, что М есть интервал [0,1], причем 0 и 1 представляют соответственно низшую и высшую степени принадлежности. Таким образом, основное предположение состоит в том, что расплывчатое множество D , несмотря на нечеткость его границы, может быть достаточно точно определено путем сопоставления каждому объекту х числа, лежащего между 0 и 1, которое представляет степень его принадлежности к D [7].

Появление аппарата лингвистической переменной стало логическим продолжением развития теории нечетких множеств. Лингвистическая переменная отличается от числовой переменной тем, что ее значениями являются не числа, а слова или предложения в естественном или формальном языке. Учитывая, что слова всегда менее точны, чем числа, понятие лингвистической переменной дает возможность приближенно описывать явления, которые настолько сложны, что не поддаются описанию в общепринятых количественных терминах. В частности, нечеткое множество, представляющее собой ограничение, связанное со значением лингвистической переменной, можно рассматривать как совокупную характеристику различных подклассов элементов универсального множества. В этом смысле роль нечетких множеств анало- гична той роли, которую играют слова и предложения в естественном языке. Например, понятие «риск электроустановки» отражает техногенную опасность объекта. Тогда термины «высокий», «низкий» и т.д. – названия нечетких множеств, образованных путем действия модификаторов «высокий», «низкий» и т.п. на нечеткое множество «риск». Отметим, что понятие «лингвистическая переменная» представляется более высокого порядка, чем нечетная переменная, в том смысле, что значениями лингвистической переменной являются нечеткие переменные. Поэтому лингвистическая переменная характеризуется набором [X, T(x), Q, G, M], в котором Х – название переменной; T(x) – обозначает терм – множество переменной Х, т.е. множество названий лингвистических значений переменной Х со значениями из универсального множества Qс базовой переменной q; G – cинтаксическое правило, порождающее название Х переменной х; М – семантическое правило, которое ставит в соответствие каждой переменной Х ее смысл М(Х), т.е. нечеткое подмножество М(Х) универсального множества Q.

Выводы

• 1.    СБЭ, являющаяся компонентом сложной человеко-машинной системы (человек ‒ электроустановка ‒ среда), обладает свойствами многовариантности и многокритериальности и функционирует в условиях недостаточности статистической информации. Наличие неопределенности (устранимой и неустранимой) в исходных данных приводит к тому, что выбор оптимального варианта СБЭ также сводится к неопределенности.

• 2.    Для оценки эффективности СБЭ (выбора критериев оптимизации в условиях неопределенности исходной информации) представляется перспективным использование нового похода, в основе которого лежит математическая теория нечетных множеств.

• 3.    Снятие неопределенностей возможно с помощью интеллектуальной системы, направленной на построение имитационных моделей процесса возникновения отказов и опасных техногенных событий и создание алгоритмов извлечения знаний из экспертных систем. Использование такого подхода менее чувствительно к нечеткости и неточности исходных данных и позволяет снизить квалификационный уровень пользователя.