Применение теории перколяции для моделирования различных процессов в системе MATLAB

В 1957 году математики Броадбент и Хаммерсли опубликовали статью, в которой поделились с читателями идеей вероятностной формализации процесса просачивания воды в перколяторе электрической кофеварки. [1] Их построение было      альтернативой      классическому

диффузионному описанию распространения одной физической субстанции, условно называемой жидкостью в другой, условно называемой средой. Так возникла новая теория, названная впоследствии теорией перколяции, или протекания (от английского глагола to percolate -просачиваться, протекать).

Перколяция характеризует широкий класс явлений      в

двухфазных

(многофазных)  системах с  контрастными физическими    свойствами    компонент:

протекание жидкостей через пористые среды, прохождение электрического тока в композитах              металл-диэлектрик, распространение фронта возбуждения в сильно неоднородных активных средах (эпидемий, лесных пожаров), передачу информации через случайные каналы связи и т.п.

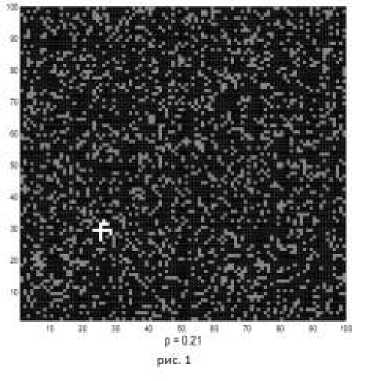
Рассмотрим классическую постановку

задачи статической перколяции. Простейшие решеточные задачи теории протекания формулируются следующим образом. Рассмотрим квадратную решетку, каждый узел которой занят с вероятностью p или пуст с вероятностью 1 - p . Вероятность p можно интерпретировать как долю

(концентрацию) занятых узлов при случайно-однородном заполнении решетки. [2] Пустые и занятые узлы могут отвечать самым разнообразным физическим свойствам, например, являться проводниками и изоляторами. Очевидно, что при малых концентрациях р<<1 проводящие квадратики либо изолированы друг от друга либо формируют небольшие группы - кластеры ближайших соседей. Два проводящих узла принадлежат одному кластеру в том и только том случае, когда они связаны проводящей цепочкой ближайших соседей.

При р<<1 система в целом демонстрирует диэлектрические свойства, поскольку не существует длинных проводящих цепей соединяющих противоположные стороны решетки. Наоборот, при p < 1 проводящей оказывается подавляющая доля пространства решетки. Существует некоторое критическое значение    p = pc, при котором происходит переход от диэлектрического состояния (при p < pc ) к проводящему при (p > pc). Критическое значение p = pc называется порогом протекания (перколяции).

Как отмечает Шредер, несмотря на простое определение, установление точного значения порога перколяции для узлов на квадратной решетке является нетривиальной задачей. Массированные расчеты по методу Монте-Карло дали значение p *0,59275, при этом количество десятичных знаков возрастет с использованием все более мощных компьютеров.

В противоположность обычным фазовым превращениям , где смена фаз происходит при некоторой критической температуре, описанный

выше перколяционн ый переход является геометрическим Перколяционный геометрическими фазовым превращением. переход характеризуется свойствами проводящих

кластеров вблизи p = p . При р<<1 существуют только кластеры небольших размеров. По мере роста концентрации p средний размер кластеров увеличивается. При концентрации близкой к критической появляется кластер, связывающий противоположные стороны решетки. Такой кластер называют перколяционным. В термодинамическом пределе бесконечно протяженной решетки перколяционный кластер называют бесконечным кластером (БК). С дальнейшим ростом концентрации доля принадлежащих перколяционному кластеру узлов (плотность перколяционного кластера) возрастает. Соответственно, средний размер конечных кластеров, не принадлежащих перколяционному кластеру, уменьшается и при p = 1 все узлы принадлежат, очевидно, только одному кластеру.

Такие задачи являются простейшими для перколяционной модели. Таким образом описание более сложных систем и структур может быть сведено к перколяционной модели с наличием большего количества различных параметров.

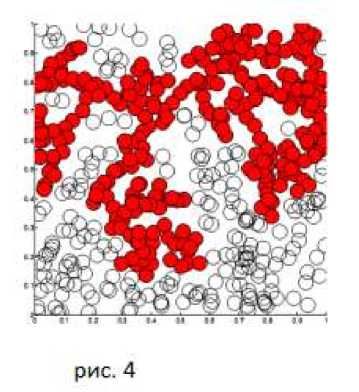
В экологии и биологии также широко применима теория протекания. Например, данная модель могла служить для нахождения времени озеленения района после пожара. В основу легла задача окружностей. Ее краткое описание выглядит так: допустим, что, на плоскости расположены окружности с одинаковым радиусом, равным R , центры которых случайно-однородно (т.е. совершенно хаотически и в среднем равномерно) распределены по плоскости. Другими словами, обе координаты центров окружностей задаются случайными числами, равномерно распределенными в интервале от нуля до L где L очень большая (по сравнению с R ) длина, характеризующая размер рассматриваемой системы. Важная отличительная черта этой задачи состоит в том, что окружности могут сколь угодно перекрываться друг с другом. В противоположность решеточным задачам дискретной перколяции, представленная постановка является типичным примером, так называемой континуальной перколяции. Будем считать, что среднее число центров окружностей, приходящееся на единицу площади (концентрация центров окружностей), равно n . Две окружности считаются связанными друг с другом, если они имеют общие точки, т.е. являются пересекающимися. Если окружность A связана с окружностью B, а B связана с C, то A связана с C. Таким образом, далекие друг от друга окружности могут быть связаны по цепочке охватывающих окружностей. Задача состоит в том, чтобы найти критическое значение концентрации n , при котором возникает протекание по связанным окружностям, т, е. возникают пути, проходящие через всю систему и состоящие из пересекающихся окружностей. Иными словами, возникает бесконечный кластер связанных друг с другом окружностей.

В пакете MATLAB была построена упрощенная динамическая модель распространения возбужденного фронта в неоднородной среде, что по сути является моделью инвазии травянистых растений.

Проблема озеленения территорий после выработки месторождений очень актуальна. Моделирование процесса инвазии лежит на стыке теоретической экологии, и теории сложных нелинейных систем. Важно подчеркнуть, что анализ структурных особенностей подобных систем не укладывается в рамки традиционных подходов и делает актуальным использование средств современной дискретной математики. Вместе с тем, попытки такого рода в биологии не многочисленны. Область эта, особенно ее "экологическая" часть, находится в начале своего становления, поэтому важность и актуальность подобных исследований несомненна. Так, например, серьезную роль в актуализации темы играют проблемы восстановления поврежденных экосистем в условиях увеличенной антропогенной нагрузки. Комплекс задач, состоящий в восстановлении структуры, функции, разнообразия и динамики специфичной экосистемы, решается путем активной реинтродукции и, в частности, путем высаживания и засевания территории растениями исходных видов. Ясно, что выявление факторов воздействующих на успех и скорость реинвазии может быть осуществлено только с применением методов математического моделирования.