Применение теории возможностей и теории вероятностей при оценке результатов моделирования боевых действий

цессов, причём к этим процессам можно смело отнести военные действия. Попытки интерпретации с помощью любого стиля математического моделирования военных действий, происшедших во Франции в мае - июне 1941 года, и особенно боевых действий немцев и бельгийцев в Эбен-Эмаэль, дают результаты, ничего не имеющие общего с реальностью [3].

Но этого мало. Главная проблема для современной практики имитационного моделирования заключается в почти полном отсутствии адекватных оценок эффективности элементарных составляющих боевых действий. Суть имитационного статистического моделирования заключается в получении априорно неизвестных статистических оценок сложных явлений на основе информации об априорно известных вероятностных характеристиках простейших элементов боевых действий [4]. При отсутствии подобной информации, что реально имеет место, статистическое имитационное моделирование становится несостоятельным [5]. Причина столь прискорбного состояния дел кроется в высокой стоимости проведения в настоящее время натурных экспериментов с реальным вооружением. Ранее таких проблем не было.

Так, например, при подготовке к принятию на вооружение зенитной ракетной системы ЗРС С-300 ПТ1 (1978 год) на полигоне было проведено более 800 пусков ЗУР за два года. При устранении замечаний, отмеченных в протоколах Государственной комиссии, было проведено ещё более 300 пусков. Статистический материал, как говорится, богатейший, хотя его всё равно не хватало для адекватного оценивания ТТХ ЗРС. Что уж тут говорить про современную ситуацию, когда массовых пусков вообще не проводится. Отметим также, что крайне убогий парк мишеней-имитаторов и мишеней-аналогов ещё более усугубляет ситуацию.

Следовательно, применение традиционных статистических методов в целом и методов имитационного статистического моделирования в частности не имеет ныне под собой надёжной эмпирической базы.

Но, допустим, что проблема с накоплением эмпирических данных каким-то образом решена. Будет ли в этом случае имитационное статистическое моделирование состоятельным и самодостаточным? Увы, сами принципы стохастического моделирования не позволяют получить те знания, которые нужны военным. Пусть, например, результаты имитационного статистического моделирования по оценке эффективности двух перспективных систем вооружения дают результаты, представленные в таблице.

Если судить об образцах вооружения по оценке математического ожидания эффективности, то первый образец предпочтительнее второго: его усреднённая оценка эффективности выше. Но если разбирать данный пример с точки зрения векторной оптимизации, то ни один из образцов не доминирует, по Парето. Таким образом, статистическое моделирование не позволяет рациональным образом сравнить два образца вооружения даже при наличии полной и достоверной информации об элементарных процессах, характеризующих функционирование этих образцов.

Таблица

Результаты имитационного статистического моделирования

№ образца вооружения	Прогнозируемая оценка эффективности (по результатам моделирования)	Оценка вероятности соответствующего значения эффективности	Оценка математического ожидания эффективности
1	0,8	0,5	0,6 (вариант предпочтительней)
	0,4	0,5

2	0,6	0,5	0,55
	0,5	0,5

По своей сути статистическое моделирование в контексте приведённых в таблице данных свидетельствует лишь о том, что при отражении большого количества совершенно идентичных ударов СВКН противника средняя эффективность для первого образца вооружения составит 0,6, а для второго - 0,55. Какая будет достигнута эффективность при отражении первого и, возможно, единственного удара противника по результатам имитационного статистического моделирования судить нельзя - сама природа статистического моделирования не позволяет этого сделать.

Но есть область научного знания, которая позволяет получить количественный прогноз эффективности при отражении, например, первого и, возможно, единственного удара противника, - это теория возможностей [6].

Теория возможностей позволяет учесть одновременно два вида неопределённости: нечёткость и случайность. В практических приложениях теория нечётких множеств хорошо работает совместно с методами теории вероятностей и математической статистики [7].

Пусть A - нечёткое подмножество множества

X = {xi}, i = 1,2,™ n со степенью принадлежности цд (х), и пусть P - вероятность события х. Тогда математическое ожидание некоторой функции f, определённой на X, для дискретного случая определяется выражением:

C p ( f , A ) = Z ' ./(-* ( x ) P ■ (1)

Предложенное определение (1) обеспечивает органическую связь теории нечётких множеств с традиционными подходами, основанными на теоретико-вероятностной интерпретации неопределённостей и позволяет более детально описывать существующие неопределённости в исходных данных, причём, при необходимости -в сочетании с методами традиционной статистики.

В настоящее время принято выделять четыре базовых вида вероятностей: классическая, частотная, логическая и субъективная [8]. При этом каждый из них удовлетворяет исходным аксиомам теории вероятностей [9]. Что же даст вероятностно-нечёткая интерпретация исходных данных, приведённых в таблице? Для 1-го образца вооружения получается результат, представленный на рис. 1. Упомянутые на рисунке гипотезы А, В, С означают: гипотеза А - результат

ВЕСТНИК 2016

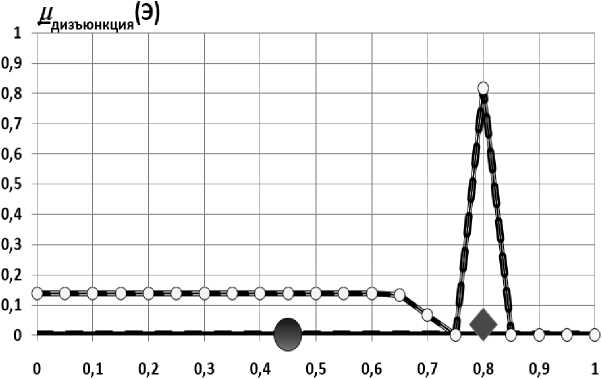
сэ - нечёткая оценка эффективности, согласованная с гипотезой А

• ■    - нечёткая оценка эффективности, согласованная с гипотезой В

^ ■ - нечёткая оценка эффективности, согласованная с гипотезой С

• * са - огибающая, полученная в результате операции дизъюнкции

• ♦    - вероятностно-нечёткая верхняя граница эффективности стрельбы для 1-го образца вооружения

• - ♦ - - оценка эффективности стрельбы для первого образца вооружения

Э - оценка эффективности стрельбы

Рис. 1. Вероятностно-нечёткая оценка эффективности стрельбы 1-го образца вооружения в первом, и, может быть, единственном, противовоздушном бою, равная 0,45

ВЕСТНИК 2016

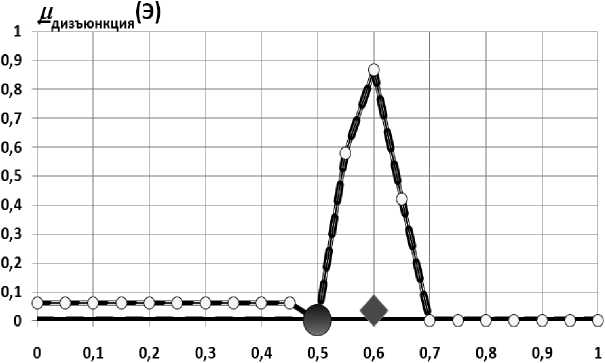
сэ - нечёткая оценка эффективности, согласованная с гипотезой А

• —    - нечёткая оценка эффективности, согласованная с гипотезой В

^■- нечёткая оценка эффективности, согласованная с гипотезой С еЗэ- огибающая, полученная в результате операции дизъюнкции

• •    - вероятностно-нечёткая верхняя граница эффективности стрельбы для 1-го образца вооружения

• - ♦ - верхняя оценка эффективности стрельбы для первого образца вооружения

Э - оценка эффективностистрельбы

Рис. 2. Вероятностно-нечёткая оценка эффективности стрельбы 2-го образца вооружения в первом, и, может быть, единственном, противовоздушном бою, равная 0,5

стрельбы близок к средневзвешенной оценке 0,6 (см. таблицу); гипотеза В означает, что результат стрельбы близок к максимальной оценке 0,8; гипотеза С означает, что результат стрельбы близок к минимальной оценке 0,4.

Для 2-го образца вооружения получается результат, представленный на рис. 2.

Таким образом, вероятностно-нечёткая оценка эффективности отдаёт предпочтение 2-му образцу вооружения, что противоречит результатам, полученным на основе чисто вероятностного подхода. Но необходимо подчеркнуть, что вероятностно-нечёткая оценка в контексте дан- ной задачи полностью согласуется с результатами максиминного и игрового подходов. И это не удивительно, потому что, согласно [6], оба указанных подхода являются частными случаями теории возможностей.

В целом необходимо отметить, что теория и практика применения вероятностно-нечёткого подхода к оценкам исхода уникальных и единичных событий даёт результаты, всегда превосходящие по точности результаты чисто вероятностного подхода. Так как в военном деле каждое ошибочное решение может оказаться для командира последним, использование вероятностно- нечёткого подхода, базирующегося на теории возможностей, имеет большие перспективы внедрения, и особенно эти перспективы хорошо просматриваются в алгоритмах АСУ управления войсками и оружием.