Применение тепловой томографии в решении задач моделирования радиолокационных изображений

объектов и целей. Одним из способов построения таких высокоточных моделей является применение специального программного обеспечения, реализующего пространственную обработку полей и целей для заданных участков местности по изображениям, полученным в видимом диапазоне длин волн с учетом матриц высот и базовых сплошных покрытий высокого разрешения. Для повышения достоверности моделей РЛИ изображения оптического диапазона длин волн должны быть классифицированы по видам материалов. Решение данной задачи в инфракрасном диапазоне длин волн представлено в работе [5].

Теоретические исследования

При прохождении электромагнитной волны через диэлектрик часть ее энергии тратится на поляризацию материала, при этом релаксационная поляризации сопровождается электрострикцией (деформацией) диэлектрика, которая пропорциональна квадрату напряженности электрического поля. В изотропных средах электрострикция описывается законом [6]

AV

Т"пр 2,

где AV/V - относительная объемная деформация; Q - электрострикционный коэффициент, характеризующий деформацию под действием индукционного поля; P – поляризация.

Под действием переменного электрического поля частотой ω диэлектрик в результате электрострикции колеблется с частотой 2и за счет двукратной (за период поля) переориентации доменов, следовательно, происходит преобразование электрических колебаний в звуковые.

Известно, что коэффициент поглощения звука для поперечных волн (возбуждаемых под действием переменного электрического поля электромагнитной волны, когда время релаксации велико по сравнению с периодом колебаний в волне) пропорционален выражению [7]

K

П

~

2 _

To а Р ct

AC

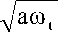
где T_o - значение температуры твердого материала без внешнего воздействия; а - коэффициент термического расширения; ρ – плотность; c – скорость распространения волны; ω – частота колебаний звуковой волны; А – среднее значение межатомных расстояний; С – теплоемкость; K П – коэффициент поглощения.

Скорость распространения электромагнитной волны зависит от показателя преломления n среды и определяется выражением

C t = с /п.

где с – скорость света;

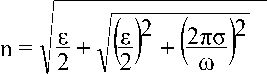
σ – проводимость, ε – диэлектрическая проницаемость [7].

Для

2no диэлектрических сред ---<< 1, и, следовательно, показатель преломления для

ω диэлектрика (4) n ~ д/е^, а выражение (3) имеет вид

ct = с/ t

Согласно определению теплового расширения

V’-V

а =----------г,

V(T2-T1)

где V - объем твердого тела при температуре T i ; V ' - объем твердого тела при температуре T₂, T 2 > T_b Используя (1) и введя подстановку AT = T 2 - T_b получим:

Р 2П

а = ^Г-AT

Тогда, произведя замену С = λ /aρ, расчетное выражение для коэффициента поглощения можно привести к виду

K

П

cQ 2Topa2 = к----2—гAA T Хе2

Р \/2ш,

где κ – параметр пропорциональности [7].

П ГОХ V

Следовательно, выражение (8) устанавливает связь между К П и теплофизическими параметрами (теплопроводность и температуропроводность) диэлектрических материалов. С использованием данной зависимости становится возможным по данным дистанционного измерения распределения теплофизических параметров приповерхностного слоя Земли и расположенных на ней техногенных объектов построить приближенную модель РЛИ.

Теоретические и экспериментальные результаты определения пространственного распределения теплофизических параметров (λ и а), полученные с использованием БЛА на основе решения задачи редукции кубоида ИК-изображений, представлены в работах [8, 9]

Методика обработки изображений

Методика обработки кубоида ИК-изображений исследуемой поверхности заключается в выполнении следующих действий:

• 1.    Получение тепловых томограмм поверхности [10, 11], К П которого является «эталонным». Полученные тепловые томограммы будут «эталонными» Т_а Э , Т ^Э .

• 2.    Получение тепловых томограмм исследуемой поверхности и при тех же режимных параметрах проведение измерений, что и в пункте 1 - Т а , Т_х.

• 3.    Преобразование тепловых томограмм по температуропроводности и теплопроводности в изображение, имеющее размерность коэффициента поглощения электромагнитной волны (ЭМВ). Используя принцип эталонирования, на основании полученных тепловых томограмм пунктов 1 и 2 изображение по K_П получают согласно (8) путем вычисления отношения

λ[i, j]a2[i, j]

Kn[i, j] =---------1-----,

П         λэ[i, j]a2[i, j]

где i, j – номера отсчетов пикселей на изображении.

В свою очередь, диэлектрические немагнитные материалы поглощают не весь объем электромагнитной энергии, часть ее отражается. Характер отражения радиоволн от земной поверхности зависит в первую очередь от электрических свойств и степени неровности (шероховатости) этой поверхности, а также от длины волны, поляризации векторов электромагнитного поля и угла падения облучающих электромагнитных колебаний.

Коэффициент отражения электромагнитных волн приповерхностного слоя Земли и поверхностных объектов определяется диэлектрической проницаемостью. Для случая нормального падения плоской волны на немагнитный диэлектрик без потерь он будет описываться выражением

-2

К_ОТ =    " Г 7-                                            (10)

ОТ (1+ ε)2

Когда плоская электромагнитная волна, распространяясь в среде, падает на границу раздела с диэлектрической средой под некоторым углом падения ф, (фП[0, п/2]), коэффициент отражения будет зависеть от ориентации плоскости поляризации ЭМВ и плоскости падения ЭМВ. При перпендикулярной поляризации, когда плоскость поляризации, содержащая направление вектора напряженности электрического поля E, перпендикулярна плоскости падения волны, коэффициент отражения для немагнитного диэлектрика будет определяться выражением

^K ОТ ⁼

(cosφ - ε -sin2φ)2

(cosφ+ ε-sin2φ)2

а при параллельной поляризации [12] -

^K ОТ ⁼

( ε -sin2φ -cosφ)2

( ε -sin2φ +cosφ)2

Значения теплопроводности λ и диэлектрической проницаемости ε некоторых материалов для длины волны, равной 3 см, представлены в табл. 1.

На основании табличных данных зависимость диэлектрической проницаемости от теплопроводности для соответствующих материалов можно аппроксимировать сплайн-интерполированным полиномом е = ГД) (рис. 1).

Использование зависимости е = f_e(Z) на основании (9) К ОТ для каждой точки (i,j) исследуемой поверхности будет описываться выражениями

K_ОТ [ i, j ] =

(cosφ - fε(λ[i, j]) - sin2φ)

(cosφ+ fε(λ[i, j])-sin2φ)2

K_ОТ [ i, j ] =

( fε(λ[i,j])-sin2φ -cosφ)2

( fε(λ[i, j])-sin2φ +cosφ)2

для соответствующих направлений вектора поляризации E.

Следовательно, используя изображения тепловых томограмм, полученных в результате дистанционного мониторинга земной поверхности с БЛА в ИК-диапазоне длин волн, на основании (13) и (14) строят приближенную модель РЛИ.

Результаты численного эксперимента

Для численной апробации представленной методики построения РЛИ в среде теплового моделирования RadTherm была разработана пространственная тепловая модель местности с известными теплофизическими характеристиками. Внешний вид тепловой модели изображен на рис. 2.

Тепловая модель включает поле, примыкающую к нему реку, дорогу, проходящую через поле, и мост через реку, а также три объекта военной техники. В результате обработки пространственной тепловой модели было получено изображение поля яркости тепловой томограммы, кластеризированное по теплопроводности [4] (рис. 3).

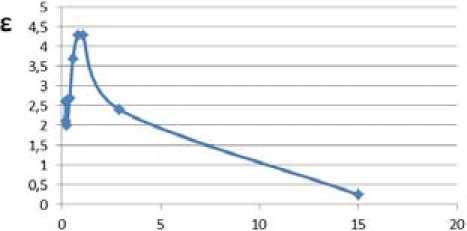
Таблица 1 Значение теплопроводности и диэлектрической проницаемости для некоторых материалов при длине ЭМВ 3 см

Номер	Материал	λ	ε
1	Керамзит	0,18	2,1
2	Гравий	0,2	2,6
3	Древесина (береза)	0,25	2
4	Полиэтилен	0,4	2,7
5	Кирпич красный	0,56	3,7
6	Известняк	0,8	4,3
7	Асфальтобетон	1,05	4,3
8	Мрамор	2,91	2,4
9	Теплопроводник	15	0,25

А, Вт/мК

Рис. 1. График аппроксимированной функциональной зависимости

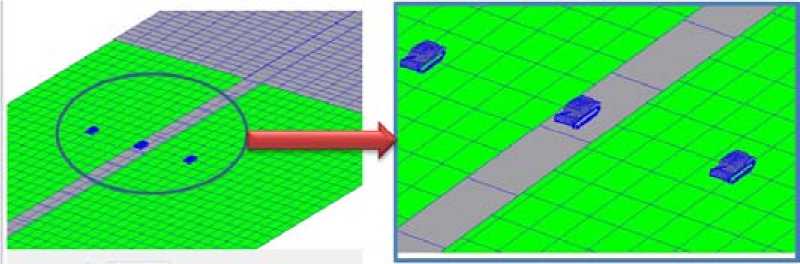
Рис. 2. Пространственная тепловая модель местности

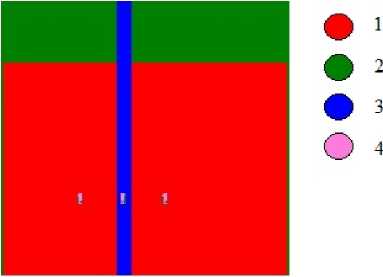
Рис. 3. Изображение поля яркости тепловой томограммы, кластеризированное по теплопроводности: 1 – земля (λ=1 Вт/мК); 2 – вода (λ=0,559 Вт/мК); 3 – асфальтовая дорога ( λ=0,72 Вт/мК); 4 – металлический объект военной техники (λ=15 Вт/мК)

Рис. 4. Модель РЛИ

На рис. 3 классифицированы земля, вода, асфальтовая дорога и три объекта военной техники.

На основании зависимости (13) пространственное распределение теплопроводности, представленное в виде поля яркости тепловой томограммы (рис. 3), получена приближенная модель РЛИ (рис. 4), адекватно отражающая пространственное распределение К ОТ .

Вывод

Таким образом, в статье представлена методика получения РЛИ земной поверхности путем преобразования изображения тепловой томограммы на основании функциональной зависимости ε = f ε (λ) при длине ЭМВ, равной 3 см. Данная методика обеспечивает получение модели РЛИ, приближенной к реальным условиям наблюдения, полученной в результате дистанционного мониторинга земной поверхности и техногенных объектов с помощью тепловизионного приемника, размещенного на БЛА в пассивном режиме.

Работа выполнена при финансовой поддержке РФФИ (грант № 15-08-02611 А).