Применение транспортных задач в электроэнергетике и решение их с помощью программы MathCAD
Автор: Эргашев Б., Дадамирзаев М.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 4 (10), 2016 года.
Бесплатный доступ
В современном мире невозможно представить развитие сферы производства без информационных технологий и современных программных обеспечений. В этой статье решены общие вопросы к выяснению как применение транспортных задач в электроэнергетике и решение их с помощью программы MathCAD
Метод транспортных задач, математическая модель, алгоритм, оптимизация, целевая функция, электрическая сеть, транспортная матрица
Короткий адрес: https://sciup.org/140268719
IDR: 140268719
Текст научной статьи Применение транспортных задач в электроэнергетике и решение их с помощью программы MathCAD
В последние время появились многие пакетные программы, с помощью появились возможность решения математических задач ( в том числе и других задач науки, описывающее такими же математическими моделями) без составления компьютерных программ. В учебном процесс ( иногда и в научных учреждениях) с помощью использованием таких систем как
MathCAD, Maple, Mat lab, Mathematic и.т.д. занятия становятся интереснее, осмысление содержания занятия более быстрое и глубокое а также на укрепление излагаемых пониятий и на решение задач остётся достаточно много времени. Из выше указанных систем, MathCAD-более проще чем остальные и она предназначено для технических вузов, а остальные, можно сказать, для профессиональных математиков. Именно в MathCAD задача формулируется в наиболее естественного математического виде, а в других математических системах шаги алгоритма решения задачи с помощью команд системы.
Как известно в MathCAD задачи решаются следующими способами [2]:
-
- с помощью внутренних функций MathCAD;
-
- с помощью математического алгоритма решения задача;
-
- с помощью алгоритма решения задачи, реализованного, во внутренним языке MathCAD.
Передем теперь общих вопросов к выяснению как применение транспортных задач в электро-энергетике и решение их с помощью программы MathCAD.
Транспортная задача – это задача отыскания таких путей перевозки продукта от пунктов производства к пунктам потребления, при которых общая стоимость перевозок оказывается минимальной.
Математический аппарат транспортной задачи применим и к задачам электроэнергетики. Здесь под продуктом подразумевается электрическая мощность, передаваемая от источников питания к потребителям по линиям электропередачи. Источниками питания являются электрические станции или подстанции, потребителями – промышленные, городские, сельскохозяйственные потребители электроэнергии. Оптимизации подлежат затраты на схему электрической сети, состоящей из линий электропередачи, связывающих узлы источников питания с узлами потребителей.
Пусть в проектируемой системе электроснабжения имеется i = 1, 2 , ... n узлов источников питания и j = 1, 2, ... m узлов потребителей. Мощность каждого из источников составляет Ai, а мощность каждого из потребителей – B j единиц мощности (е. м.). Известно взаимное расположение узлов источников и потребителей. Стоимость передачи единицы мощности от источника i к потребителю j (удельная стоимость) составляет z ij у. е. /е. м.
Общее количество возможных к строительству линий электропередачи, связывающих источники с потребителями, составляет nm . Мощности, передаваемые по этим линиям, являются искомыми переменными x ij , следовательно, количество искомых переменных составляет nm .
Затраты на электрическую сеть равны сумме произведений удельных стоимостей на величины передаваемых мощностей от источников i к потребителям j . Поэтому подлежащая минимизации целевая функция имеет следующий вид: n
Z = E z u* x u ^ min (1)
i = 1
С позиций теоретической электротехники электрическая сеть является электрической цепью и для этой сети применимы все законы, известные из курса электротехники, в частности 1-й закон Кирхгофа. Для каждого i-го источника питания сумма мощностей, оттекающих по линиям ко всем j = 1, 2, ... m узлам потребителей, равна мощности А i этого источника:
E x u ^ A- (2)
i = 1
Для каждого j-го потребителя сумма мощностей, притекающих по линиям от всех i = 1, 2, ... n источников, равна мощности Bj этого потребителя
Z x y ^ B (3)
i = 1
Соотношения (2) и (3), представляющие собой балансы мощности в каждом из узлов, являются ограничениями при решении транспортной задачи. Общее количество ограничений равно количеству узлов источников и потребителей n + m. В рассматриваемой постановке транспортной задачи все искомые мощности xij, передаваемые от источников к потребителям, являются неотрицательными. Следовательно, граничные условия имеют вид:
x ij > 0, I = 1, 2 , ... n; j = l, 2, ... m. (4)
Выражения (1), (2), (3) и (4) представляют собой математическую модель транспортной задачи. Видно, что выражения целевой функции (1) и ограничений (2) и (3) являются линейными.
Особенности транспортной задачи следующие:
-
1) все ограничения имеют форму равенств;
-
2) все коэффициенты при переменных в системе ограничений равны плюс единице;
-
3) каждая переменная дважды входит в систему ограничений: один раз в балансы узлов источников (2), второй раз в балансы узлов потребителей (3).
С учетом этих особенностей для решения транспортных задач разработаны специальные методы решения, более простые, чем другие методы решения оптимизационных задач.
Рассмотрим решение транспортной задачи методом потенциалов на конкретном примере.
Пример 1. В проектируемой системе электроснабжения имеется два узла с источниками питания и три узла потребителей. Мощности источников составляют А 1 и А 2 , а мощности потребителей - В 1 , В 2 и В 3 , е. м. Взаимное расположение узлов и возможные к сооружению линии электрической сети показаны на рис. 1. Удельные затраты на передачу мощностей по линиям между узлами источников и потребителей составляют z 11 , z 12 , z 13 , z 21 , z 22 , z 23 у. е. /е. м.
Составить математическую модель для решения транспортной задачи.
Решение. Целевая функция, представляющая собой суммарные денежные затраты на электрическую сеть, в соответствии выражением (1) будет иметь вид:
Z = z 11 ·x 11 + z 12 ·x 12 + z 13 ·x 13 + z 21 ·x 21 + z 22 ·x 22 + z 23 ·x 23 → min.
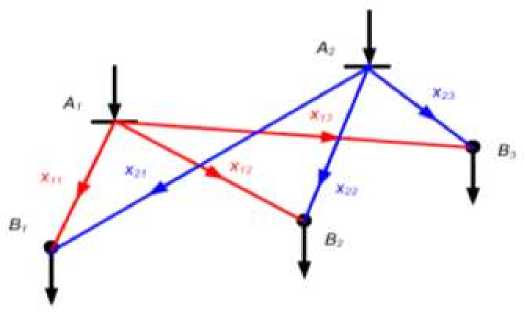
Рис. 1. Взаимное расположение источников питания и потребителей
Ограничения, представляющие собой балансы мощности в узлах электрической сети, в соответствии с выражениями (2) и (3) будут иметь следующий вид:
x11 + x12 + x13 = A1, x21 + x22 + x23 = A2, x11 + x21 = B1, x12 + x22 = B2, x13 + x23 = B3.
Граничные условия в соответствии с соотношением (4) запишутся как x11 > 0, x12 > 0, x13 > 0, x21 > 0, x22 > 0, x23 > 0.
Полученные выражения представляют собой математическую модель транспортной задачи для схемы, приведенной на рис. 1.
При решении транспортных задач удобно пользоваться табличной формой записи. В этом случае ограничения (2) и (3) записывают в виде транспортной матрицы размерностью nm . Для рассмотренного выше примера 1. транспортная матрица представлена в виде табл. 1.
Таблица 1.
Исходное решение
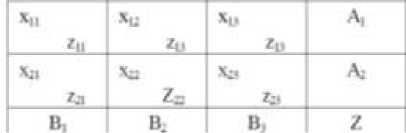
Справа указаны заданные мощности источников А 1 и А 2 , снизу -заданные мощности потребителей В 1 , В 2 и Вз , справа внизу - значение целевой функции Z. Непосредственно в клетках транспортной матрицы записаны подлежащие определению искомые переменные x ij и заданные значения удельных стоимостей передачи мощности z ij .
Каждая i-я строка матрицы соответствует уравнению баланса мощности i-го источника питания, каждый j-й столбец – уравнению баланса мощности j-го потребителя.
Исходное допустимое решение может быть получено по алгоритму минимальной удельной стоимости:
-
1. В транспортной матрице выбирается клетка с минимальным значением z ij . Если имеется несколько таких клеток, то выбирается любая из них.
-
2. В выбранную клетку в качестве базисной переменной заносится наименьшая из двух величин А i или B j , т. е. x i j = min(A i , B j ). При этом выполняется баланс мощности по строке i или столбцу j , в которые входит переменная x ij .
-
3. В остальные клетки строки i или столбца j , для которых выполнен баланс мощности, заносятся нули, соответствующие свободным переменным. Большая из двух величин А i и B j условно заменяется разностью этих двух величин.
-
4. Из оставшихся незаполненных клеток транспортной матрицы вновь выбирается клетка с минимальным значением z ij . Далее пункты 2 и 3 повторяются до полного заполнения всех клеток транспортной матрицы.
Следует напомнить, что общее количество переменных составляет nm . Количество отличных от нуля базисных переменных составляет (n + m – 1). Количество равных нулю свободных переменных составляет (nm – (n + m–1)).
Теперь найдем оптимальное решение для задачи примеры при следующих исходных данных:
A 1 = 50, А 2 = 30, B 1 = 20, В 2 = 25, В: = 35 е. м.
z 11 = 1,2; z 12 = l,8; z 13 = 1,5;
z 21 = 1,6; z 22 = 2,3; z 23 = 1,9.
По выше показанным исходным данным математическая модель выражается следующим образом.
Целевая функция:
Z= 1,2x 11 + l,8x 12 +1,5x 13 +1,6x 21 +2,3x 22 +1,9x 23 →min
Ограничения:
|
x 11 1 |
+ x 12 |
+ x 13 |
= 50 |
|
I x 21 |
+ x |
+ x 13 |
= 30 |
|
' x ii |
+ x 21 |
= 20 |
|
|
1 x 12 |
+ x |
= 25 |
|
|
V ( x 13 |
+ x 23 |
= 35 |
Граничный условия:
x 11 >0, x 12 >0, x 13 >0, x 21 >0, x 12 >0, x 22 >0, x 23 >0
Приведённая транспортная задача математической модели решим с помощью MathCad.
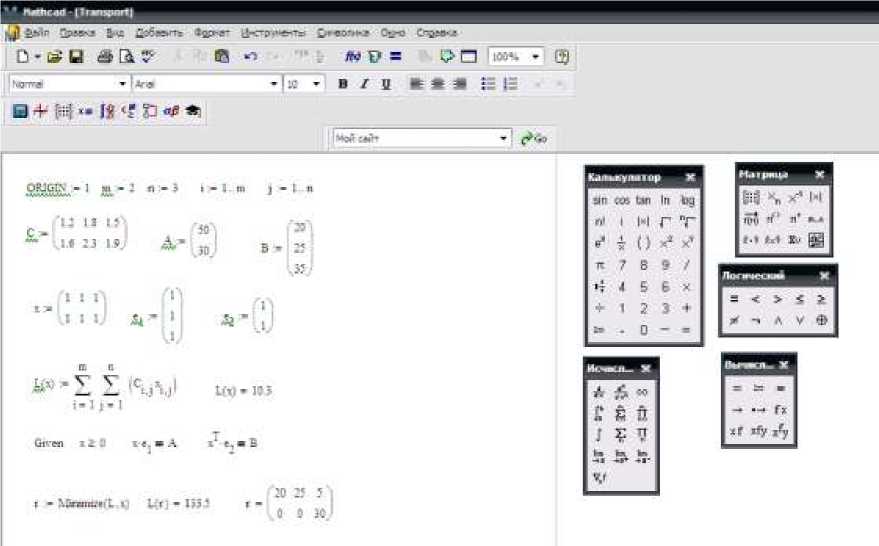
Список литературы Применение транспортных задач в электроэнергетике и решение их с помощью программы MathCAD
- Костин. В.Н Оптимизационный задачи электроэнергетики/ В.Н.Костин.- СПб., 2003.- 120 с.
- Ракитин, В.И. Руководство по ВМ и приложения MathCad. М.:ФМ, 2005.- 264 с.
- А.И.Имамов, Б.С.Эргашев. Реализация схемы Кранка- Николсона для линейного параболического дифференциального уравнения в MathCad. Молодой учёный №14 (73), Сентябрь, 2014 г.-с 1-5.


