Применение уравнений нейтрального равновесия к задаче о цилиндре, сжатом боковым давлением

Введение. Согласно феноменологическому подходу, принятому в механике сплошных сред, базовые соотношения для нелинейно-упругих тел включают конкретное представление удельной потенциальной энергии деформации. Предлагаемое выражение должно допускать описание основных нелинейных эффектов и приводить к доступному математическому рассмотрению простых деформаций. На свойства резиноподобных материалов сильно влияют химический состав и процессы изготовления. Для некоторых сортов резины подходит модель несжимаемого упругого материала, конкретизированная потенциалами Муни, Трелоара, Г.М. Бартенева и Т.Н. Хазановича, К.Ф. Черных и И.М. Шубиной [1]. Однако часто необходим учет сжимаемости материала. Как практический, так и теоретический интерес в этом случае представляет потенциал Блейтца и Ко. Целью данной работы является исследование устойчивости равновесия толстостенного цилиндра из этого материала при гидростатическом сжатии на основе трехмерных уравнений нелинейной теории упругости.

Определяющие соотношения и начальная деформация нелинейно упругого цилиндра. Закон состояния задается выражением плотности потенциальной энергии деформации, предложенным в работах Блейтца и Ко [2, 3]:

Здесь /„ /2, /3 - главные инварианты меры деформации Коши-Грина, коэффициенты а, р, ц — модули упругости. Константа а выражается через постоянные Ламе и коэффициент Пуассона:

X _ v 2ц 1 - 2v

Трехконстантный закон состояния (1) удачно подходит для описания упругих свойств некоторых сортов резины, требующих учета сжимаемости.

Далее будет использован закон состояния для напряжений в форме Фингера [1]:

aw^ aw т awA aw

--Е +  + Л \F F ai; 1 ai^

ai^

где T - тензор напряжений Коши; E - единичный тензор; F - мера деформации Фингера Выражение тензора Т, найденное с учетом потенциала (1), принимает вид:

Обобщенные модули задаются равенствами:

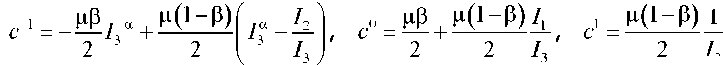
Рассматривается осесимметричная деформация кругового полого цилиндра

Материальные координаты - цилиндрические координаты точки недеформированного цилиндра -г, ф, z. Координаты точки после деформации, возникающей за счет поверхностного нагружения равномерно распределенным давлением по наружной боковой поверхностям цилиндра, обозначены соответственно R. Ф, Z. Место точки в актуальной конфигурации определяется выражениями:

R = R(f)e_r + dzi₃, Ф = ф.                               (3)

Здесь er, e z3 - базисные векторы цилиндрических координат; г, ф, z-радиус, азимуталь- ный угол и высота соответственно. Введем обозначения:

a = R, о = —.

г

Тогда градиент деформации, определяемой соотношениями (3), принимает вид

о

VR =

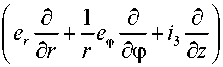
R = ае_ге_г + 6е_фе_ф + di₃i₃.

О где V - набла-оператор в отсчетной конфигурации. Отсюда находим меру Фингера и главные инварианты:

1₃=сг№.  (5)

F = a1erer+b2elfelf+d\i3, I; = I^F^ a2+b2+d2, I2=a2

Тензор напряжений является соосным мере Фингера и с помощью физических компонент [1] выражается в виде:

Т = <зее_г + <5ее +о LL, г г г (р ф (р z 3 3 ' где, учитывая формулы (2) и (3), для физических компонент можно получить следующие выражения:

Q

а

₌ ц(1-Р) 7 3/2 ⁷3

₌ ц(1-Р) 7-3/2 ⁷3

= ц(1-Р)

7 3/2

1^3

1+“ - v

В соотношениях (6) инварианты вычислены по формулам (5), a vt =——

Если отсутствуют массовые силы, условие равновесия в объеме имеет вид

\ ок К ГО   oZ F                ’

Учитывая зависимости (6) и деривационные формулы [1], можно это условие свести к одному уравнению do, a /

—L +—(o, -o dr rbx

Поскольку в этом уравнении напряжения ог, оф определены формулами (6), то ясно, что (7) -это нелинейное дифференциальное уравнение второго порядка. Приведем вариант уравнения, отвечающий упрощенному варианту потенциала (1), - материалу Ноулса-Стернберга (а = 1/2, Р = 0, v = l/4):

da a-b

--1-- dr Ъг

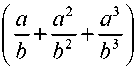
Условия равновесия на цилиндрических поверхностях имеют вид:

|0, ог = <

где гв - внутренний радиус трубы; гн - наружный радиус; р - интенсивность давления. В ча стности, для материала Ноулса-Стернберга ог =ц| 1—

( a bd )

Краевое условие на торце удовлетворяется интегрально, в «смысле Сен-Венана»:

Q = f aabrdr ,

где Q - продольная сила, приложенная к торцам цилиндра для равновесия. Окончательно задача Ламе для цилиндра определяется краевой задачей (7), (9). Причем параметр осевого смещения точек d задается в соответствии с условием (10). В упрощенном случае материала Ноулса-Стернберга задача Ламе для нелинейно-упругого цилиндра рассмотрена в [4].

Для решения нелинейной краевой задачи (7), (9) предложен численный метод, использующий конечные разности [5]. Выбираются равноотстоящие узлы, производные аппроксимировались центральными разностями. Узловые значения аргумента определяются формулами:

r=r+(i-2Ah / = 2 3  ^ + 2 h = ——-.

Используем также еще две «законтурные» точки r_v = r_B-h, r_N+3 = r_H+h. Обозначим x. значения искомой функции R^ на выбранной сетке значений аргумента. Тогда, в частности, из (7) имеем систему ^+l нелинейных алгебраических уравнений:

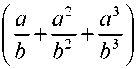
1/ _х h²(а-ЬА

X = —I X     X 1 Ч--------— j т \ >+i где а = —---—, b = —. Еще два условия определим из краевых условий:

2Н г.

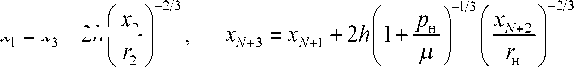
х. = х„ - 2h I —

Таким образом, имеем систему ^ + 3 алгебраических уравнений с ^ + 3 неизвестными. Решение системы получено методом простых итераций [5]. В качестве нулевого приближения итерационного метода решения краевой задачи на сетке принимались узловые значения соответствующего решения задачи Ламе для цилиндра в линейной теории упругости. Такой выбор обусловлен тем, что при малой относительной толщине оболочки и небольших давлениях уравнения (7), (8) и (9) переходят в соотношения линейной теории, для которых известны точные решения [6].

Следует отметить, что в упрощенном варианте материала Ноулса-Стернберга допускается решение дифференциального уравнения (8) в аналитическом виде. Его можно переписать, учи-d a-b d            _ тывая тождество — =--, следующим образом dr г db

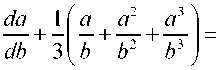
„                       а  _                  da , dt   db a-b

Применим подстановку t = —. С помощью тождеств — = t+b— и — =--- b                        db db    dr    г

последнее диффе^

ренциальное уравнение можно представить в виде:

dr _          dt г      (t-1) У(?2 +t + 4)

Отсюда находим

з

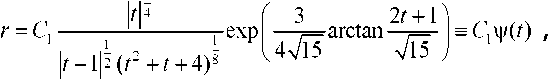
(И)

где Q - произвольная постоянная

Далее, учитывая равенство — = г

ItZR t R

получаем другое дифференциальное уравнение

dR _ dt (7^1Хг^Г+7+4) "

Отсюда имеем

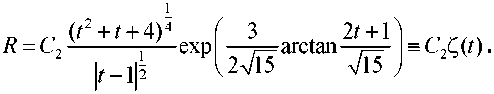
Выражения (11) и (12) дают общее решение исходного дифференциального уравнения (8) в параметрической форме. Для решения краевой задачи необходимо удовлетворить краевым условиям (9) и найти границы изменения параметра t и L(t,Hr„ t hl Y Эти значения пара-I   •         I   I  DH^VDD''HH^{,          1}

метра t определяются из системы двух нелинейных уравнений, вытекающих из краевых условий (9):

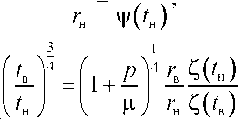
Далее, изменяя параметр t от г_в до /_н, с помощью (11) и (12) можно определить зависимость R(r) . В [4] указаны полученные ранее другими авторами параметрические формулы общего решения дифференциального уравнения (8). Однако соотношения (11), (12) имеют отличия, связанные с выбором параметра. Также в [4] не прояснен вопрос решения краевой задачи. Точное решение сходной нелинейной краевой задачи Ламе для сферы из материала Ноулса-Стернберга приведено в[7].

Уравнения нейтрального равновесия. Вектор добавочного перемещения возьмем в виде, допускающем несимметричные формы выпучивания:

W = и(г, ф, zy_r + v(r, ф, z^e^ + w(r, ф, zX .

Применяя деривационные формулы, для градиента вектора добавочной деформации имеем равенство

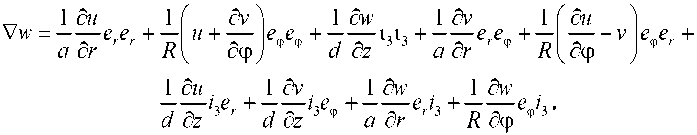
Смежные формы равновесия цилиндра исследуем с помощью оператора А.И. Лурье 0 [1,6], который для материала Блейтца и Ко определен соотношением (10), полученным в работе [7]. Учитывая это соотношение и равенство (13), для тензора © имеем следующее представление:

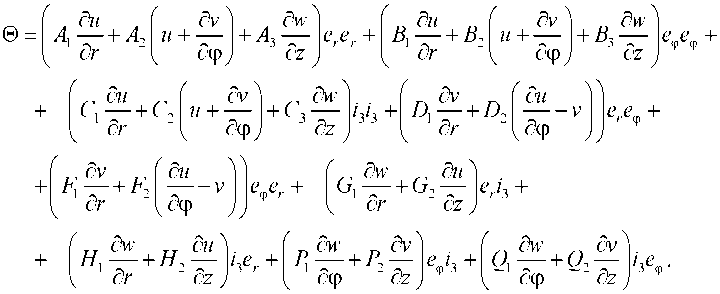
Коэффициенты при неизвестных и, v, w а их частных производных известны после решения начальной задачи Ламе функции переменной г. Приведем выражение одного из этих коэффициентов:

4 ⁼ⁱ^^((l + 2a)vi/₃^ +(2а-1)/<^1+а) + v₁27₃ ^d¹)

Уравнения нейтрального равновесия в объеме [1] (V@ = 0) приводят к системе трех ли нейных дифференциальных уравнений второго порядка с переменными коэффициентами:

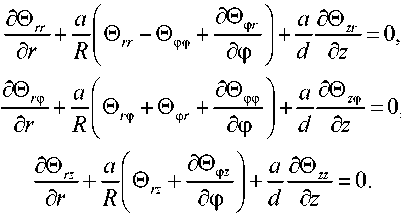
В уравнениях системы (15) компоненты тензора © выражены в соответствии с представлением (14). Нейтральное равновесие на боковой поверхности определяется условием [1,6]

N®^-p^7wN-N^w^TY                   (16)

где V - набла-оператор в метрике деформированного состояния; N - вектор внешней нормали к деформированной поверхности, нагруженной гидростатическим давлением интенсивности р. На торцах принимаем граничные условия вида при z = 0 и z = L( L- длина цилиндра):

w-0, 0rz-0zr-O.                             (17)

Соотношения (17) означают недопустимость добавочного перемещения в осевом направлении и отсутствие трения на торцах [8]. Эти равенства не противоречат характеру нагружения цилиндра наружным давлением и сжатия с торцов абсолютно жесткими гладкими плитами.

Разыскиваем решение краевой задачи (15), (16)

м = ^ (г) cos лер cos Xmz,

< ^v = ^Y„mWrn^osX_mz,                          (18)

Л = z™(r)C0STOPsinV> где п и Хт - параметры волнообразования, в соответствии с (17) определяется равенством

. кт

Х_т = — , а числа п, т - целые.

Подстановка (18) в уравнения (15) и краевые условия (16) приводит к разделению переменных. В результате получаем однородную систему обыкновенных дифференциальных уравнений:

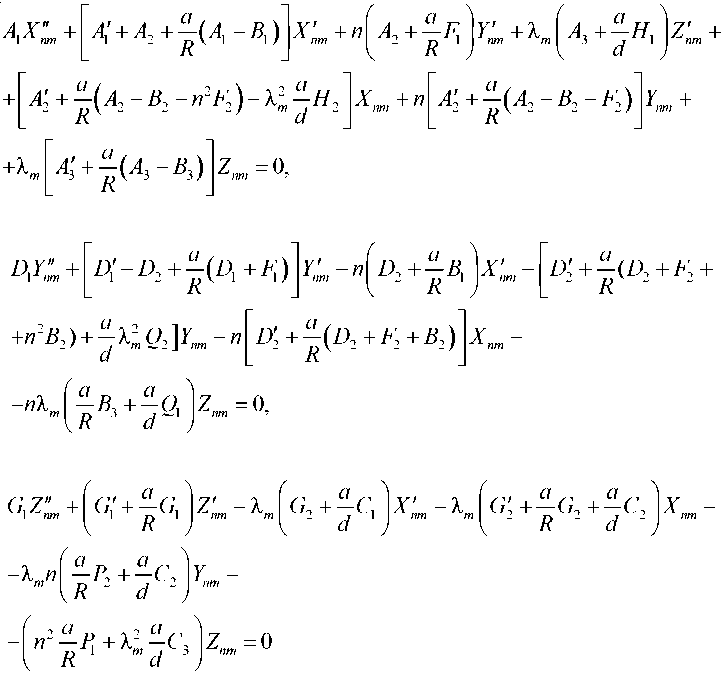
Из краевых условий (16) после разделения переменных получим при г = гв и г = гн:

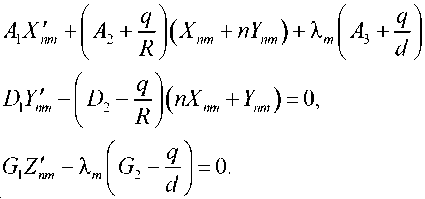
7 —О

В условиях (20) о = 0, если г = г , и а = р , если г = г .

Однородная система (19) и краевые условия (20) выражают нейтральное равновесие цилиндра. При бифуркационных значениях параметров р и d возможны нетривиальные решения краевой задачи (19), (20). Они соответствуют возмущенным равновесным формам цилиндра. Критические значения давления находим как наименьшие бифуркационные значения р при надлежащем выборе п и Х_т . Бифуркационные значения - собственные числа задачи (19), (20). Отметим, задача на собственные значения является нелинейной, поскольку искомый параметр входит нелинейно через функцию R(ry Для решения такой задачи на собственные значения использован численный метод [8].

Выводы. Численный алгоритм определения бифуркационных нагрузок, включающий решение задачи Ламе о начальной деформации цилиндра, вычисление коэффициентов системы (19) и по- лучение собственных значений, реализован на ЭВМ. Расчеты проводились как для упрощенного варианта материала - материала Ноулса-Стернберга, так и для полного закона Блейтца и Ко. В качестве примера применения полученных уравнений нейтрального равновесия рассматривались некоторые случаи потери устойчивости, изучаемые в теории оболочек [9]. Для очень длинных цилиндрических оболочек под внешним боковым давлением критическая нагрузка разыскивалась в виде соотношения Грасгофа-Бресса: ^ = 2ц(1 + у)^е3, где е - относительная толщина оболочки, р, - безразмерный параметр давления. Обнаружено, что критическому (минимальному) давлению отвечают плоские формы выпучивания: и = 2, т = 0. Представления о влиянии нелинейности на величину верхнего критического давления в зависимости от относительной толщины отражены в табл. 1. Данные второй строки согласуются с результатами, приведенными в [8]. Численный анализ также показал, что для не слишком толстостенных цилиндров влияние на критическое значение параметра давления точности решения начальной задачи (задачи Ламе) и константы р незначительное. Изучался случай оболочек средней длины, где принималось ^- = 0,38. Для таких оболочек критическая нагрузка разыскивалась в соответствии с формулой Саусвелла-Папковича: р = 2ц(1 + у)/л,е25. Длина оболочки неизменная (<2 = 1), цилиндр нагружен внешним боковым давлением. Критические значения параметра давления и соответствующие значения параметров волнообразования содержатся в табл. 2, параметр т = 1.

Таблица 1

s = 2(r -г„)/(г + г)	0,05	0,10	0,20
Р. (v= 0,272)	0,26	0,27	0,29
Р. (v= 0,250)	0,34	0,36	0,38

Таблица 2

s = 2(г -г„)/(г + г)	0,05	0,10	0,20
п	4	3	3
Р. (v= 0,272)	0,38	0,39	0,44
Р. (v= 0,250)	0,49	0,52	0,56