Применение устойчивого оценивания в задачах анализа выживаемости

Классические статистические методы оценивания параметров моделей, например, метод максимального правдоподобия, строятся, как правило, исходя из предположения о каком-либо определенном законе распределения наблюдений. На практике закон распределения часто неизвестен и реальное распределение наблюдений может отличаться от постулируемого (модельного). В результате названные методы теряют оптимальность, что может привести к неустойчивости оценок.

Для решения этой проблемы разработаны различные подходы, приводящие к устойчивым (робастным) методам оценивания. Один из таких подходов, предложенный А. М. Шурыгиным1, приводит к оценкам, которые обладают устойчивостью к асимметричному засорению модельного распределения. Среди получаемых в рамках данного подхода оценок2 условно оптимальные и обобщенные радикальные для плотности распределения минимальных значений.

В данной работе рассмотрим сравнение робастных оценок, обладающих как устойчивостью, так и высокой эффективностью, с классической оценкой максимального правдоподобия (ОМП) на примере решения задачи анализа выживаемости мышей, облученных радиацией. Использовались следующие устойчивые оценки: равнооптимальная (ОРО), радикальная (ОР) и максимальной устойчивости (ОМУ)3.

Имеются данные наблюдения времени жизни мышей (в днях), подвергшихся радиационному облучению в 300 радиан (единица измерения ионизи- рующего излучения). Всего обследовано 38 мышей в возрасте 5–6 недель. Распределение времени жизни мышей можно аппроксимировать законом Вейбулла–Гнеденко.

Исходные данные4: 317, 318, 399, 495, 525, 536, 549, 552, 554, 337, 558, 571, 586, 594, 596, 605, 612, 621, 628, 631, 636, 643, 647, 648, 649, 661, 663, 666, 670, 695, 697, 700, 705, 712, 713, 738, 748, 753.

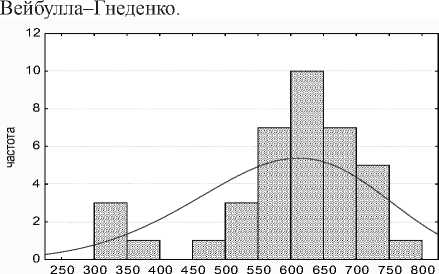
На рис. 1 представлена гистограмма плотности распределения жизни мышей, подвергшихся облучению в 300 радиан, а также линия аппроксимации данных законом Вейбулла–Гнеденко по методу максимального правдоподобия.

Для оценивания параметров распределения Вейбулла–Гнеденко прологарифмируем исходные данные и перейдем к распределению минимальных значений, при этом параметр формы будет соответствовать обратному значению параметра масштаба, а исходный параметр масштаба – экспоненте параметра сдвига.

В качестве критерия точности рассчитанных оценок используем показатели дисперсии для распределений по закону минимальных значений и Вейбул- ла–Гнеденко соответственно:

(1), где θ – оценка масштаба распределения минимальных значений.

Вестник Омского юридического института. 2010. № 2 (13)

D w = Я ²

V

Г 1 + ^ I - г| 1 I _

V к 7 V к

(2),

где Я , к - оценки масштаба и формы распределения

Рад

Рис. 1. Распределение времени жизни облученных радиацией мышей

В табл. 1 мы видим, что при распределении по закону минимальных значений робастные оценки сдвига и масштаба сосредоточены в диапазоне [6,489; 6,493] и [0,1048; 0,1102] соответственно. В то же время ОМП для сдвига и масштаба существенно отличаются и равны соответственно 6,469434 и 0,134332. При этом оценки дисперсий распределения минимальных значений для ОРО, ОР и ОМУ ниже на 39,1, 32,7 и 33,6 %, чем для ОМП соответственно.

В случае распределения Вейбулла–Гнеденко (см. табл. 2) оценка дисперсии для ОМП также уступает ОРО, ОР и ОМУ на 32,6, 26,8 и 27,5 % соответственно.

Чем меньше показатель дисперсии, тем уже соответствующие доверительные интервалы оценок параметров.

Для сравнения рассчитанных оценок (1) – (2) используем относительный показатель дисперсии относительно оценки дисперсии ОМП:

D

RaD = ---

D OMP           (3).

Таблица 2

Оценки параметров, дисперсий и относительных дисперсий распределения Вейбулла–Гнеденко (все наблюдения)

Параметры	ОМП	ОРО	ОР	ОМУ
Форма	7,444227	9,536115	9,074495	9,136484
Масштаб	645,1182	660,0541	657,9013	658,7647
Дисперсия	9227,415	6217,026	6751,384	6687,105
Относительная дисперсия (в %)	100,0	67,4	73,2	72,5

* Жирным шрифтом выделены значения показателей, превосходящие по качеству соответствующие оценки МНК

В таблицах 1 и 2 представлены оценки параметров, дисперсий и относительных дисперсий распределений минимальных значений и Вейбулла–Гнеденко.

Таблица 1

Оценки параметров, дисперсий и относительных дисперсий распределения минимальных значений (все наблюдения)

Показатели	ОМП	ОРО	ОР	ОМУ
Масштаб	0,134332	0,104865	0,110199	0,109451
Сдвиг	6,469434	6,492322	6,489055	6,490366
Дисперсия	0,029683	0,018089	0,019976	0,019706
Относительная дисперсия (в %)	100,0	60,9	67,3	66,4

* Жирным шрифтом выделены значения показателей, превосходящие по качеству соответствующие оценки МНК

Возникает вопрос: какая же оценка ближе к истинному значению параметров распределения? Для ответа вернемся к рис. 1, где мы видим, что слева на некотором расстоянии от основной массы наблюдений находятся четыре крайних наблюдения. Исходная выборка может содержать ошибочные данные5, например, вместо исходного наблюдения 337 должно быть 557. Удалим четыре крайних слева наблюдения и посмотрим, как изменятся рассчитанные оценки, а также оценки дисперсий распределений. Результаты представлены в таблицах 3 и 4.

Таблица 3

Оценки параметров распределения минимальных значений (без четырех крайних наблюдений слева)

Параметры	ОМП	ОРО	ОР	ОМУ
Масштаб	0,09247	0,100956	0,101953	0,107811
Сдвиг	6,497993	6,49444	6,493605	6,491095

⁵ См.: Boudt K. Там же.

Актуальные вопросы математики и иформационных технологий

Окончание табл. 3

Дисперсия	0,014065	0,016765	0,017098	0,019119
Относительная дисперсия (в %)	100,0	119,2	121,6	135,9

Таблица 4

Оценки параметров распределения Вейбулла–Гнеденко (без четырех крайних наблюдений слева)

Параметры	ОМП	ОРО	ОР	ОМУ
Форма	10,81434	9,905309	9,808466	9,275494
Масштаб	663,8083	661,4535	660,9017	659,2448
Дисперсия	5010,325	5830,888	5925,119	6518,073
Относительная дисперсия (в %)	100,0	116,4	118,3	130,1

Сопоставляя таблицы 1, 2 и 3, 4, заключаем, что удаление четырех крайних слева наблюдений исходных данных существенно уменьшило ОМП масштаба на 0,04186 (31,16 %) и увеличило оценку сдвига на 0,02856 (0,44 %). Робастные оценки оказались более устойчивыми. Так, ОРО масштаба уменьшилась на 0,00391 (3,73 %), а ОРО сдвига увеличилась всего на 0,002118 (0,03 %). При этом относительные оценки дисперсии распределения минимальных значений для ОРО, ОР и ОМУ больше, чем для ОМП, на 19,2, 21,6 и 35,9 % соответственно, а для распределения Вейбулла–Гнеденко – на 16,5, 28,3 и 30,1 %.

Исследование показало, что устойчивые оценки заметно превосходят по качеству и устойчивости МНК-оценку и ОМП даже при небольших объемах выборки (40–50). Главные достоинства робастных методов заключаются в том, что они не только устойчивы к аномальным наблюдениям и неправильно подобранным модельным плотностям, но и обладают меньшей дисперсией, нежели другие методы.

При удалении подозрительных наблюдений из набора данных робастные оценки в меньшей степени изменяют свои значения, в отличие от МНК-оценки и ОМП. Последние оценки при удалении становятся ближе к робастным оценкам.