Применение вариативного представления клапанных пружин для моделирования динамики МГР ДВС

В основе разработанного метода моделирования динамики МГР лежит обобщенная математическая модель («Динамика»), разработанная на кафедре автотракторных двигателей ВолгГТУ. Расчет сил, действующих в МГР, и законов движения его деталей осуществляется на основе представления последних в виде дискретных масс, котороые связаны безынерционными упругими элементами, и численного решения системы дифференциальных уравнений, описывающих движение каждой массы [6].

В базовой динамической модели каждая клапанная пружина представлена цепочкой из 6-ти сосредоточенных масс (одна масса пружины неподвижна, а другая отнесена к массе клапана), соединенных упругими связями (см. рис. 1, а). Разработанная математическая модель предусматривает возможность вариативного представления пружин. В дополнение к многомассовому подходу также реализовано представление клапанных пружин в виде эквивалентных стержней (сосредоточенные массы с распределенными параметрами), способных совершать продольные колебания (см. рис. 1, б). Допустимость такого представления следует из бо- лее точной теории расчета пружин, где винтовая пружина рассматривается как тонкий пространственный криволинейный брус. Преимуществом такого подхода является то, что процесс распространения волн напряжений в материале клапанной пружины может быть рассмотрен с позиции основных форм колебаний, которые являются определяющими при оценке нагруженности МГР. Для моделирования этих колебаний продольными колебаниями стержня должно быть соблюдено равенство значений массы и продольной жесткости пружины соответствующим величинам стержня. Применение такой схемы, помимо уточнения закона движения клапана, дает возможность более точно оценивать на-груженность самих клапанных пружин [3].

Программа для расчета вибраций клапанных пружин и их влияния на динамику МГР была реализована в виде отдельного расчетного модуля ( SPR ), работающего совместно с базовой динамической моделью.

Действующие на клапан со стороны пружин усилия упругих деформаций определялись в ходе численного решения уравнения колебаний их витков [3; 4] с соответствующими начальными и граничными условиями внутри модуля SPR . Уравнение колебаний витков получило вид

5²U К; ф ) + 2 ц d U К; ф )

дф ²      го дф

2 a\ го )

д ² и К; ф ) д^ ^{2     ,}

где U – продольное смещение сечения эквивалентного стержня от положения статического равновесия, мм;

m – коэффициент вязкого сопротивления (принимает значения в диапазоне 20…30, если не используется внешний пружинный демпфер);

x – безразмерная длина (отношение расстояния сечения от начала рабочего участка пружины до рассматриваемого сечения к полной длине пружины);

j – угол поворота распределительного вала, рад.;

w – частота вращения распределительного вала, рад/с;

a – относительная скорость распространения волн деформации по длине пружины, с^-1.

Удобно использовать нулевые начальные данные в качестве начальных , так как в начале движения клапан закрыт и неподвижен, перемещения витков пружины равны нулю. Граничные условия: перемещение примыкающего к опоре витка равно нулю, а движение подвижного конца клапанной пружины определяется движением клапана.

В основу разработанной программы был положен метод последовательных приближений, позволяющий исследовать динамику клапанной пружины на установившемся режиме. Расчет первого цикла начинался с положения статического равновесия витков. Начало отсчета по углу поворота распределительного вала соответствовало моменту начала подъема клапана при полностью устраненном тепловом зазоре. Исходная переменная – перемещения сечений пружины U ( X ; j ) - определялась интегрированием величины относительных деформаций витков h ( X ; j ) вдоль приведенной длины пружины x:

Г ю^⁴ i

U Й; ф ) = 1 —l j n ( ^ ; Ф у ) d ^ ,          (2)

V a / о

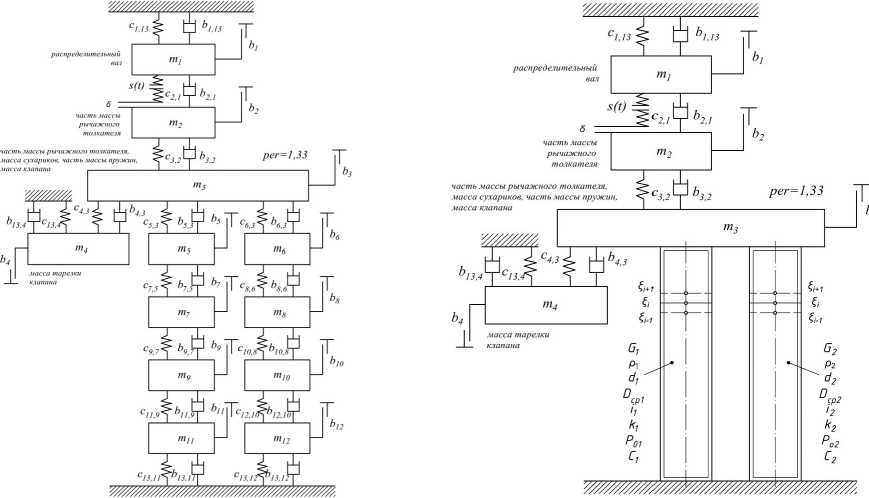
а                                                     б

Рис. 1. Расчетные схемы для исследования динамики МГР:

а – исходная динамическая модель (клапанные пружины представлены цепочкой дискретных масс); б – предлагаемая модель (клапанные пружины представлены в виде эквивалентных стержней)

Расчет продолжается до тех пор, пока не будет достигнут установившийся режим работы МГР, реализованный внутри итерационного цикла, и будет найдено периодическое решение. Решение считалось установившемся и процесс итераций, как только различие начальных данных итерации и ее конечных результатов становилось меньше заданных погрешностей расчета. По достижении установившегося режима были определены действующие на клапан со стороны пружин усилия

P. = PX^, ф)=pol + ci— nj^, ф), a

P c . = P ci .     Ф ) = P o d . + c d. — П d. ( ^ , Ф ), (3)

aâ             , где P0н. и P0в. – величина усилия предварительной затяжки наружной и внутренней клапанных пружин соответственно, Н;

c_н. и c_в. – жесткости наружной и внутренней клапанных пружин соответственно, Н/мм;

a_н. и a_в. – скорость распространения волн деформаций в наружной и внутренней пружинах соответственно, с^-1;

( а н V U h        ( а в}д U e

• ⁿ h. =1 ^_ Гяё" и ⁿ в. =1 ^_     - OTHOCU-

• V го J 5^         I ® 7 d^

тельная деформация наружной и внутренней клапанных пружин соответственно, мм

Таким образом, применительно к данной задаче взаимодействие базовой модели исследования динамики D и расчетного модуля SPR в пределах одного шага расчета по углу поворота распределительного вала ф сводится к определению ускорения, скорости и перемещения клапана, а также всех действующих на него усилий путем численного решения уравнений движения дискретных масс, занесением значения скорости клапана в качестве граничного условия для решения волнового уравнения (1) в модуль расчета нагруженнос-ти клапанных пружин SPR, определение величин перемещения сечений и относительных деформаций витков, а затем и действующих на клапан со стороны клапанных пружин усилий Pн. и Pв. и передача их обратно в D для расчета нагруженности МГР и определения действующих результирующих усилий

На рисунке 2 в качестве примера приведены полученные расчетно значения усилий от наружной и внутренней клапанных пружин, действующих на клапан, в первой основной форме колебаний при частоте вращения распределительного вала n = 2 068 об/мин Как видно, процесс колебаний не прекращается после посадки клапана на седло и продолжается до следующего подъема клапана

Оценка адекватности разработанной математической модели динамики МГР и модуля расчета вибраций клапанных пружин SPR производилась по соотношению дисперсий адекватности и воспроизводимости и осуществлялась путем сравнения экспериментальных, полученных при обработке результатов скоростной киносъемки [1], и расчетных средних пиковых значений перемещений сечений витков < U > для наружной клапанной пружины при зазорах в клапанном приводе 0 и 0,1 мм Критерием адекватности служил критерий Фишера Предлагаемая модель показала хорошую сходимость с экспериментальными данными

После вычисления действующих на клапан со стороны клапанных пружин усилий на основе разработанного метода была оценена нагруженность клапанного привода и проанализировано влияние способа представления клапанных пружин на точность получаемых результатов при исследовании его динамики

На рисунке 3 приведена диаграмма усилий, действующих на клапан, при различных способах представления клапанных пружин: каждая пружина представлена 6-ю сосредоточенными массами (см рис 3, кривая 1 ), что соответствует 12-тимассовой динамической модели (см рис 1, а); пружины представлены в виде эквивалентных стержней (см рис 3, кривая 2 ) Сопоставление производилось с экспериментальными данными, полученными при тензометрировании [2] (см рис 3, кривая 3 )

Следует отметить, что ранее исследователями было установлено: способ разбиения клапанной пружины на сосредоточенные массы и их количество существенно влияет на достоверность получаемых результатов при расчете динамики МГР Для адекватного отражения нагруженности МГР достаточно, чтобы каждый виток клапанной пружины был представлен отдельной массой, а увеличение числа масс только усложняет динамическую модель и не ведет к повышению точности получаемых результатов [5]. Это позволяет учесть влияние всех форм колебаний пружины на динамику МГР. В работе [2] показано, что 12-тимассовая модель, при которой каждая клапанная пружина представлена цепочкой из шести масс, дает наиболее адекватные и близкие к эксперименту результаты.

В соответствии с диаграммой (см. рис. 3) предлагаемая комбинированная методика дает лучшую аппроксимацию к экспериментальным данным благодаря уменьшению разницы между расчетными и эмпирическими данными, что особенно хорошо видно во второй половине диаграммы, на стороне посадки клапана. Это обусловлено тем, что представление клапанных пружин в виде эквивалентных стержней позволяет более точно определить нагружен-ность самих клапанных пружин и действующие с их стороны на клапан усилия, а следовательно, дает возможность более адекватно оценить состояние клапанного привода в целом.

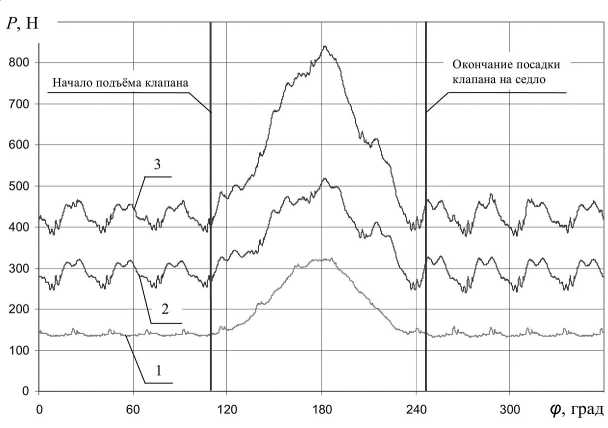
Рис. 2. Действующие на клапан со стороны клапанных пружин усилия при частоте вращения распределительного вала n = 2 068 об/мин:

1 – усилие внутренней пружины; 2 – усилие наружной пружины; 3 – суммарное усилие клапанных пружин

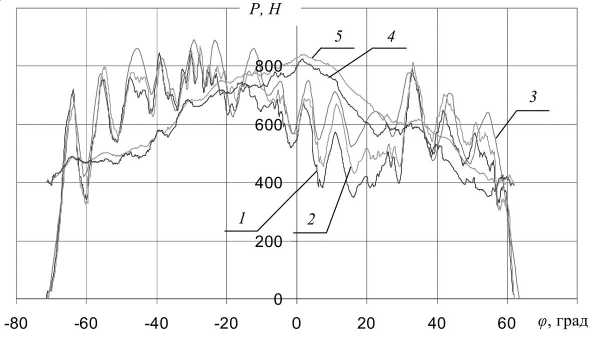
Рис. 3. Усилие в клапанном приводе при частоте вращения распределительного вала n = 2 068 об/мин:

1 – пружины представлены цепочкой масс; 2 – пружины представлены в виде эквивалентных стержней;

3 – эксперимент; 4 – суммарное усилие клапанных пружин (пружины представлены цепочкой масс);

5 – суммарное усилие клапанных пружин (пружины представлены в виде эквивалентных стержней)

Разработанная математическая модель показала хорошую сходимость расчетных и экспериментальных данных в диапазоне изменения частоты вращения распределительного вала n = 157…2 100 об/мин (см. рис. 4, кривые 2, 3).

Максимальное расхождение средних пиковых значений усилий < P > в клапанном приводе при представлении клапанных пружин эквивалентными прямолинейными стержнями (см. рис. 4, кривая 2) с экспериментальной кривой (см. рис. 4, кривая 3) составило около 7 % (при n = 1 368 об/мин), в то время как при методике, предполагающей представление пружин в виде цепочки дискретних масс, оно достигло величины 12 % (при n = 2 068 об/мин).

Средняя величина уточнения пикового усилия, действующего на клапан со стороны рычага, по предлагаемой методике равна 2 %. Наибольшие величины уточнения имеют место при более высоких частотах вращения распределительного вала (4…6 % при n = 1 538…2 100 об/мин).

Из рисунка 4 видно, что сходимость с экспериментальными данными улучшается по мере роста частоты вращения распределительного вала. Следовательно, предлагаемую методику расчета можно экстраполировать и на более высокоскоростные режимы работы двигателя и рекомендовать для исследования динамики клапанного привода современных высокооборотных автомобильных ДВС.

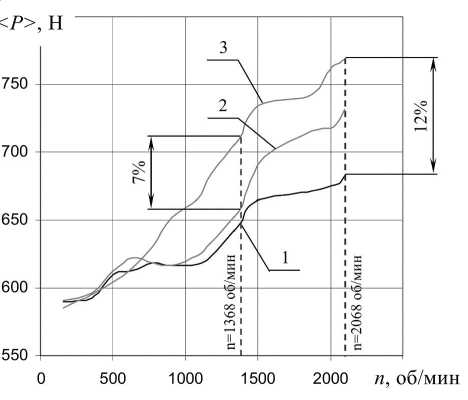
Рис. 4. Среднее пиковое усилие в клапанном приводе:

1 – клапанные пружины представлены цепочкой из 6-ти масс;

2 – клапанные пружины представлены в виде эквивалентных стержней; 3 – эксперимент

Таким образом, разработанная математическая модель, дающая возможность различными способами представлять клапанные пружины, представляет собой комбинированную методику, которая сочетает в себе преимущества как многомассового подхода (простота, оценка влияния высоких форм колебаний на динамику МГР при увеличении числа масс), так и метода эквивалентного бруса (более точная оценка напряженного состояния клапанных пружин). Она позволяет оперативно вносить изменения в структуру расчетной схемы и менять ее параметры, сохраняя при этом простоту, а также уточнить нагрузки, действующие в клапанном приводе.