Применение вейвлет-анализа для идентификации строения газовых факелов

Для точного управления процессом горения необходимо провести идентификацию структуры факела. Строению различных видов факелов посвящено большое количество работ [1–5], но все они основаны на квазистационарном подходе. Однако квазистационарные представления о строении факелов исчерпали себя, и поэтому стали развиваться методы изучения динамической структуры таких турбулентных объектов.

Из них наиболее эффективными являются: метод анализа главных компонент (МАГК), PIV-метод, дисперсионный и частотный анализ, вейвлет-анализ.

МАГК (PCА – Principal Component Analysis) нашел широкое применение при обработке многомерных данных в разных отраслях: в криминалистике при распознавании человеческих лиц, при сжатии изображений и т. п. [6].

Основное свойство главных компонент состоит в том, что при сохранении свойства ортогональности для них главные компоненты расположены в пространстве так, что соответствуют направлениям максимальной вариации первоначальных данных. Однако физическая интерпретация результатов МАГК затруднена. Также необходимо помнить, что МАГК не обеспечивает полного разделения информации о структурах и шумах.

Метод PIV (Particle Image Velocimetry) состоит в обнаружении перемещения частиц на последовательности изображений. Его современная интерпретация заключается в том, что PIV является наиболее быстрым методом нахождения кросскорреляции [7]. К недостаткам PIV-метода следует отнести трудность физической интерпретации его результатов, а также большие временные затраты при вычислениях.

При дисперсионном и частотно-фазовом анализе обрабатывается последовательность оптических изображений, полученных путем фоторегистрации контрольной области турбулентного потока. Фоторегистрация может производиться в различном диапазоне длин волн излучения в зависимости от задачи исследований.

При излучении явлений теплопереноса фоторегистрацию производят в инфракрасной части спектра, чтобы выявить структуры, участвующие в теплообмене.

При дисперсионном анализе [7] для каждой точки (пикселя) оптического изображения вычисляется дисперсия (стандартное отклонение) контрольного параметра. При этом под когерентным турбулентным образованием, точнее под областью потока, где оно существует, понимается зона, в которой дисперсия имеет одинаковую величину. Эта область визуализируется цветом или чернобелым шаблоном заливки, чтобы получить видимую структурную картину потока. Основным недостатком дисперсионного анализа является отсутствие информации о частоте пульсаций контрольного параметра, что не позволяет строить структурно-иерархические модели турбулентности.

При частотно-фазовом анализе, основанном на быстром преобразовании Фурье, обработка оптической информации в случае тепловизионного фильма производится по следующем алгоритму [7, 8]: для каждой точки матрицы строится временной ряд, состоящий из отдельных элементов (число которых равняется количеству кадров съемки), после чего этот ряд обрабатывается по быстрому преобразованию Фурье.

При этом под структурным образованием в турбулентном потоке (факеле) понимается область, где контрольные параметры пульсируют с одинаковой характеристической частотой и в одной фазе [7, 8]. Под характеристической понимается частота, соответствующая главному максимуму в собственном спектре пульсаций контрольного параметра. Таким образом, пиксели исходных матриц, в которых контрольный параметр пульсирует с одинаковой частотой и фазой, считаются относящимися к одному турбулентному образованию. Такая интерпретация имеет явное физическое обоснование, в чем и состоит её достоинство. К существенному недостатку частотно-фазового анализа следует отнести отсутствие возможности получения информации об изменении частоты пульсации во времени.

При структурном подходе к изучению турбулентности и, в том числе, иерархическом её построении, целесообразно применение вейвлет-преобразования для получения новой информации о закономерностях структурообразования.

Вейвлет – это математическая функция, позволяющая анализировать различные частотные компоненты данных. График этой функции выглядит как волнообразные колебания с амплитудой, уменьшающейся до нуля вдали от начала координат. Однако это частное определение; в общем случае анализ сигналов производится в плоскости вейвлет-коэффициентов.

Вейвлет-преобразование является интегральной операцией, представляющей собой свертку сигнала вейвлет-функцей, и таким образом, служит способом преобразования функции (или сигнала) в форму, которая делает некоторые величины исходного сигнала более поддающимися изучению или позволяет сжать исходный набор данных. В принципе, вейвлет-преобразование сигналов является обобщением спектрального анализа [8, 9].

Описание экспериментальной установки

Для изучения строения факелов применялась экспериментальная установка, схема которой показана на рис. 1.

Для создания прямоточных факелов использовалось классическая инжекционная горелка, внутренний диаметр смесительного канала которой равнялся 17 мм, а его длина составляла 50 мм.

Для создания закрученной струи в том же канале размещался специальный аксиальный завихритель с плоскими лопатками. Отличие этого завихрителя в том, что у него отсутствует центральная втулка, как в традиционных конструкциях. Применение такого завихрителя обусловлено тем, что он создает более мощную зону обратных токов, которая позволяет значительно расширить диапазон устойчивого горения. Массовый расход газа G определялся с помощью электронных весов.

Для измерения поля температур факелов использовался тепловизор NEC TH9100. Данные с тепловизора по интерфейсу FireWire передавалась на персональный компьютер и записывались на жесткий диск при помощи программного обеспечения, поставляемого комплектно с тепловизором.

Тепловизор передавал экспериментальные данные о поле температур в программу NEC Image Processor. При помощи этой программы записывался тепловизионный фильм c частотой 30 Гц, каждый кадр которого переводился в матрицу c расширением «csv». Таким образом, тепловизионный фильм преобразовывался в массивы температур, с размерностью 240 x 320 x 970 (240 и 320 означают длину и ширину в пикселях, а 970 – число кадров).

Обработка этих массивов производились с помощью специальной программы, которая была написана в среде MathWorks – MATLAB версии

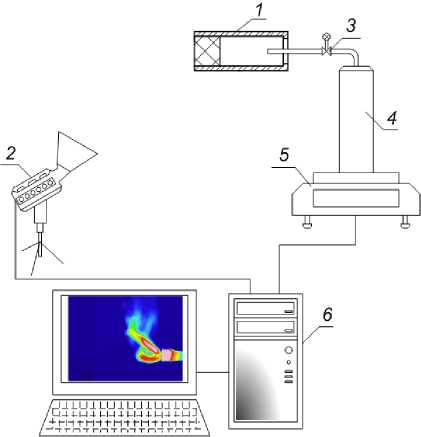
Рис. 1. Схема экспериментальной установки для изучения газовых факелов: 1 – опытная горелка; 2 – тепловизор;

3 – газовый вентиль; 4 – баллон с топливом; 5 – электронные весы; 6 – персональный компьютер

R2012b. Для минимизации вычислительных затрат и увеличения точности, массив температуры был разделен на временные фрагменты, которые были равны 512 кадрам, т. е. отдельный массив температур состоял из 512 матриц.

После обработки временного ряда формировались матрицы векторов, которые визуализировались цветом.

Результаты обработки различными методами

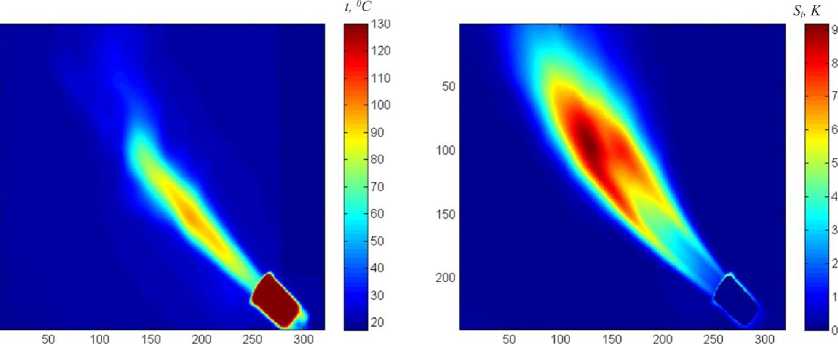
На рис. 2 представлены результаты идентификации структуры свободного прямоточного газового факела, выполненной дисперсионным и частотнофазовыми методами. Напомним, что в качестве контрольного параметра использовалась температура.

Было установлено существование в прямоточном факеле зон, в которых температура пульсировала с одинаковой частотой, но в разных фазах.

Наблюдения динамической картины показали, что когерентные образования непрерывно перемещаются в зоне факела, переходя из одной области в другую, т. е. наблюдался эффект пространственно-временной перемежаемости.

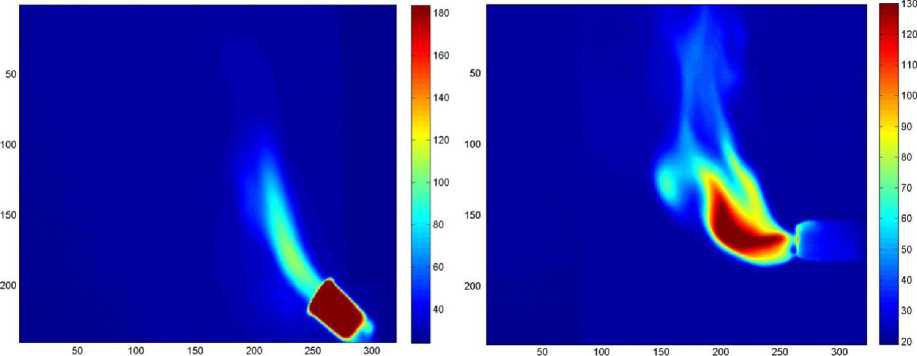
На рис. 3 представлена визуализация структуры свободных и закрученных факелов, полученная с помощью вейвлет-анализа. При выполнении дискретного вейвлет-преобразования использованы два разных базиса – Добеши и Хаара [9, 10]. В целом результаты, полученные при этих различных базисах, отличаются друг от друга незначительно.

Сразу отметим, что проявилось одно из самых важных достоинств вейвлет-преобразования – фильтрация шума, что позволило получить наиболее чистые (самодостаточные) результаты.

Изображения на рис. 3 соответствуют низким частотам, а высокочастотная область представлена на рис. 4.

Показательно, что применение вейвлет-анализа позволяет выделить более мелкие вихри или их совокупности, кроме того, появляется возможность отследить их эволюцию в потоке.

Следует отметить, что изображение для высоких частот является более информативным (см. рис. 4).

На высокочастотном изображении отчетливо видно различие в строении факелов: прямоточный факел содержит группу подвижных мелкоячеистых

а)                                                               б)

в)                                                                          г)

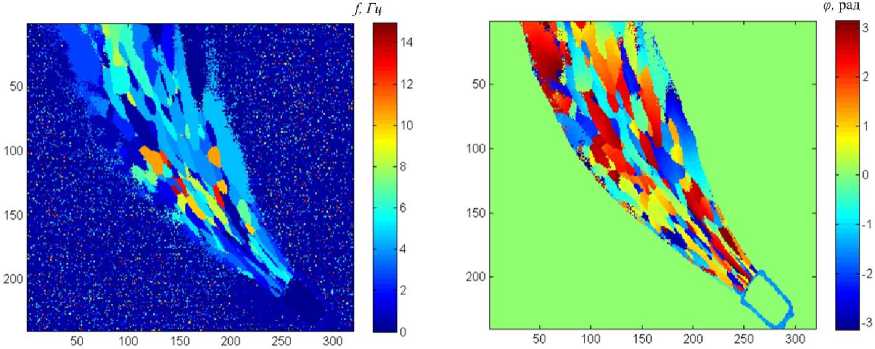
Рис. 2. Тепловизионное изображение свободного одиночного газового факела (шкала температур условна) (а); стандартное отклонение температуры S_t (б); характерные частоты пульсаций f (в); фаза пульсации φ (г).

Топливо (смесь): изобутан 80 %, бутан 15 %, пропан 5 %

а)                                                               б)

Рис. 3. Результаты вейвлет-анализа свободного (а) и закрученного (б) факелов (низкие частоты) ( G _г.а = 0,024 г/с, G г.б = 0,023 г/с). Топливо: а – смесь: изобутан 80 %, бутан15 %, пропан 5 %; б – бутан 100 %. Завихритель (б) с углом установки лопаток 45°

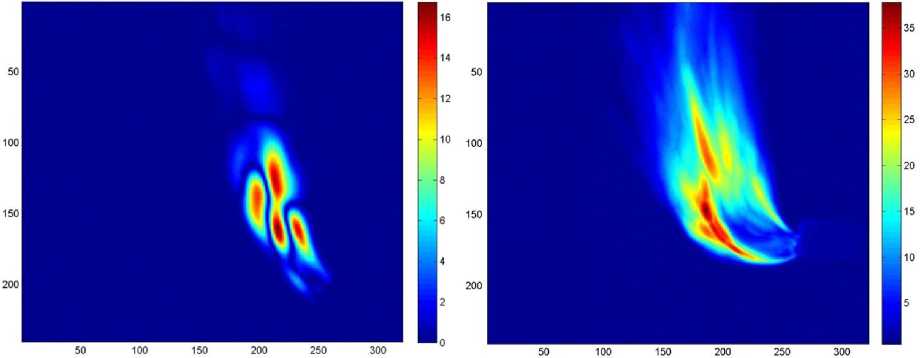
а)                                                               б)

Рис. 4. Результаты вейвлет-анализа свободного (a) и закрученного (б) факелов (высокие частоты) ( G _г.а = 0,024 г/с, G _г.б = 0,023 г/с). Топливо: а – смесь: изобутан 80 %, бутан 15 %, пропан 5 %; б – бутан 100 %. Завихритель (б) с углом установки лопаток 45°

структур, а в закрученном факеле просматриваются крупномасштабные структурные образования, т. е. термомеханика процессов существенно различна.

При данном виде преобразования также проявился упомянутый эффект перемежаемости.

Нужно отметить, что применение непрерывного вейвлет-преобразования в сравнении с дискретным требует больших временных затрат: вычисления происходят на несколько порядков дольше.

Конечно, пока нельзя дать убедительную физическую трактовку результатов вейвлет-анализа, поскольку сама теория динамической структурной турбулентности находится лишь в стадии зарождения. Но безусловно, они несут принципиально новую информацию о структурах, накопление которой сейчас крайне необходимо.

Выводы

Основываясь на полученных результатах, можно сделать следующие выводы:

– Не существует какого-либо предпочтительного метода компьютерной идентификации турбулентных структур: каждый из них дает новую, иную информацию о когерентных образованиях в газовом потоке, которая в каждом конкретном случае может быть наиболее значимой.

– Не определены критерии исходного выбора метода структурного анализа под определенную задачу, что объясняется отсутствием достаточно разработанной теории динамической структурной турбулентности.