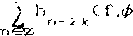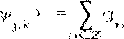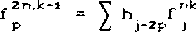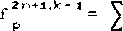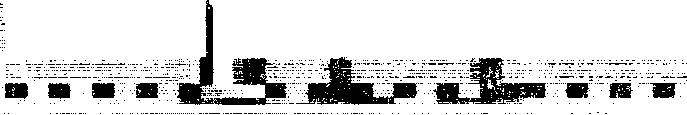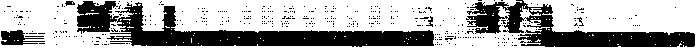Применение вейвлет-анализа к задачам исследования загрязнения окружающей среды

Recently a new type of functional basis has been introduced in analysis, wavelets, which permit an analysis both in physical space and in scale space. A short review 03 main properties of wave let-transform is done. The method is applied to data of atmosphere pollution. The choice of best basts to obtain a minimal number of basis functions is discussed.

Среди задач по метеорологическим аспектам загрязнения атмосферы наибольший интерес представляют вопросы краткосрочного и долгосрочного прогноза состояния окружающей среды. Задачи прогноза требуют построения модели сложной нелинейной системы, зависящей как от многочисленных метеорологических, так и техногенных факторов. В этой связи большое значение приобретают исследования закономерностей пространственно-временного распределения концентраций примесей, что стимулирует в свою очередь использование разнообразных методов для анализа аэрометрических данных. Среди прочих используется и спектральный анализ, но его возможности в таких задачах весьма скромны и сводятся к выявлению достаточно очевидных периодических составляющих, соответствующих суточным, недельным иди годовым циклам газ. На практике встречаются ситуации, когда чередуются различные типы суточной изменчивости концентраций и необходимо разделить соответстующие временные интервалы, .либо требуется выделить разовые выбросы, происходящие на фоне периодических и квазипериодических сигналов. При построении математической модели процесса заманчиво иметь базис, подстраивающийся под текущую структуру сигнала.

Альтернативой фурье-анализу становится возникший совсем недавно математический аппарат, названный вейвлет-анализом и уже успешно конкурирующий с анализом Фурье в таких' областях, как обработка и синтез сигналов и изображений, распознавание образов, исследование функциональных операторов и сложных многомерных полей, изучение турбулентности и др. В основе вейвлет-анализа лежит представление исследуемой функции по базису, каждая функция которого характеризует как определенную временную с пространственную:* частоту, так и место ее локализации во времени с пространстве:*. Это достигается за счет выбора специальных функций - вейвлетов с wavelet - небольшая волна, рябь:*. локализованных как в физическом пространстве, тек и в пространстве частот и получаемых друг из друга путем масштабного преобразования и сдвига.

Идеи использования функций, попадающих под opieделение тевлета, высказывались в разное время разными авторами и посходят по сути к работам Хаара 1900 года, но целенаправленное развитие теории вейвлетов началось после работ А. Гроссмана и Ж.Морле газ с 1984г.з, стимулированных проблемами обработки результатов сейсмических наблюдений. К настоящему времени число статей по вейвлетам превысьдо 1000, имеются обзоры гт* и монографии г 6,isj. К сожалей: вейвлет-анализ мало известен в нашей стране, хотя после работы Зимина 1981г.гзз, подложившего для описания турбулентности иерархический базис с фактически вейвлет-базис), еще до появления теории вейвлетов была выполнена большая серия работ, в которых система разномасштабных функций использовалась не только для анализа, но и для моделирования нелинейных процессов в развитой турбулентности, с Обзор этих рабОТ СМ. В С 4.815

Цель данной статьи состоит в том, чтобы, кратко изложив основные идеи вейвлет-анализа, рассмотреть возможности его применения к задачам исследования аэрометрических данных. Особое внимание уделяется проблеме выбора базиса, оптимального с точки зрения описания системы с помощью минимального числа функций.

ВЕИЬ.ГГЕТЫ. .Мая вейвлет-функция v*_ab 'данного семейства получается из единственной "материнской" функции v путем сжатия растяжения^-* и сдвига:

-1/2      -1 .        . . .

V . к= а ¥* а '■ х ~ b) > где ^арачотр а е к* - масштабный множитель. отвечающий за ширину ве^З/ю^а и г -s к - параметр сдвига, соответствующий наложению вейвлета. Таким образом, все функции базиса должны быть самоподобны и, l частности, имеют постоянное число осциляций. Благодаря этому условию, вейвлет-преобразование дает хорошее пространственное разрешение при малых масштабах и хорошее частотное разрешение при больших.

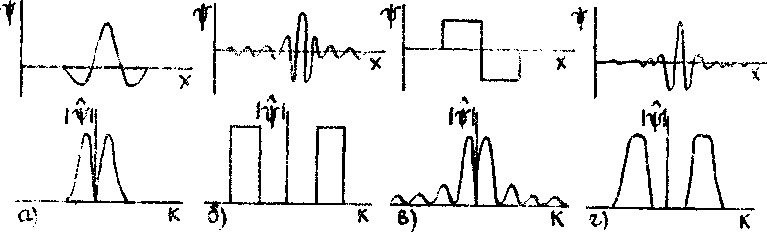
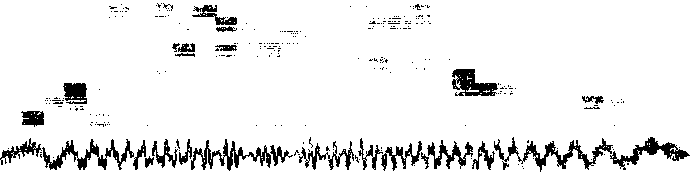
0 Формальной точки зрения семейство вейвлетов можеч строиться на основе любой функции ^ удовлетворяющей условию fy

-00

На практике вейвлет должен также быть хорошо локализован как в физическим пространстве, так и в пространстве частот. Дл» этого достаточно, чтобы функция у- была сконцентрированна б некоторой конечной области и была достаточно гладкой. Специфика локализации различных функций в физическом и Фурье-пространствах показана на рис. i.

Рис. 1 сао Вейвлет мексиканская шляпа; сбэ функция лиглвуда--Пеом. с во функция Хэара-, его вейвлет Мейера.

Необходимо отметить особенности вейвлет-преобразования, выгодно отличающие его от преобразования Фурье. Последнее распределяет сингулярные возмущения по всему спектру частот, тем самым делая очень трудным или даже невозможным изучение локальных свойств сигнала из его фурье-образа. Если эти возмущения имеют случайный характер. то их практически невозможно отфильтровать. Вейвлет-преобразование сохраняет локальность подставления сигнала и позволяет локально его и восстановить. Возможно ^конструировать только часть сигнала или выделить вклад, определенного масштаба. Если вейвлет -коэффициенты подвержены случайным ошибкам. они будут действовать на реконструируемый сигнал локально вблизи положения возмущения. Свойства вейвлет-анализа обусловливают' его эффективность для выделения в сигнале непериодических и квазипериодических (труктур различно!о временного и/или пространственного масштаба.

НЕПРЕРЫВНОЕ И ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ. Непрерывное вейвлет-преобразование *<а,ьэ функции гсх). х е к есть w<. a.bD - (у ,13 = . л       -----IfCxDdx,         СЗ)

J           , a j

Условие саз гарантирует обратимость преобразования: должна существовать по крайней мере одна формула для точной реконструкции сшнала из его вейвлет-образа. В качестве примера функции, используемой для непрерывного преобразования, приведем веивлет Марра с мексиканская шляпах, который является второй производной Функции Гаусса: ч<^ = ci-х²зех_Р<-х²/г>срис. id.

Характерной особенностью непрерывного преобразования является его избыточность, вытекающая из того, что пространство функций одного переменного отображается в .двухмерное пространство ■ масштаб-коирдинатах, и проявляющаяся в наличии корреляции между веивлет-коэффициентами. Непрерывное преобразование эффективно применяется для анализа многомерных полей, обработки изображений и звуковых сигналов. Избыточность делает его устойчивым к возможным случайным возмущениям, однако корреляции между коэффициентами могут привести к неверной интерпретации результатов преобразования исследуемого сигнала. Кроме того, его реализация требует значительных вычислительных ресурсов.

Б случае дискретного вейвлет-преобразования масштабный параметр а и параметр сдвига ь принимают дискретные значения: а = Э^т. b = nb a^m, С т.п е Z; а >1; Ь >О 0. ТОГДа О        ОО             о    о        ^м

С х?

-т/2 о

о

nb a J > о о

а

-т.

О

Zy< а

О

пЬ о

Дискретное вейвлет-преобразование позволяет избавиться от избыточности непрерывного благодаря существованию функций, образующих полные ортонормированные базисы пространства lArj б случае, если а_о= г и ь_о= 1. Кроме того, в рамках дискретного преобразования при выполнении некоторых дополнительных требований удается построить быстрый алгоритм получения вейвлет-коэффициентов - так называемый анализ с переменным разрешением С mul t i гe$ol ut.1 on anal ysi sD [ 1 ОЗ .

Анализ с переменным разрешением основывается на рассмотрении последовательности вложенных друг в фуга аппроксимирующих функциональных пространств

V с V с V с V с V с . . .          С

2      1      О      -1     -2

таких, что

U V = 1?С R> , jeZ

Л Z ■= <0>-jeZ J

Дополнительным требованием, непосредственно связанным с понятием переменного разрешения, является то. что все пространства являются масштабированной версией центрального пространства vr/ т. е.

V.*=*fC2Jx0e V .

Таким образом, подпространство v явля. гея подпространством функций, аппроксимирующих l²cr> с разрешением 2^J и переход от пространства v к пространству v соответствует переходу к большим масштабам. т. е. огрублению функции с естественной потерей некоторой информации, содержащейся в исходной функции.

Основная идея анализа с переменным разрешением состоит в построении алгоритма, использующего разность информации, содержащейся в различных масштабах. Для любого j е z, определяется подпространство w, - ортогональное дополнение v в v^:

C7>

V

J -1

= V н> W , V j. W и w J. W , при j * i ' .1             .1 J j                        J J

Кроме того, из свойства сто следует, что l²crd = е*_л где все w ортогональны друг другу. Очевидно, подпространствам w, также присуще масштабное свойство с Для любой последовательности замкнутых подпространств, удовлетворяющих условиям с 4-ет, существует вейвлет-функция у. такая, что множество 2"^,/2v<2'^jx - кТ. к е Z> Образует ОрТОНОрМИрОВЭННЫЙ бЭЗИС подпространства w, для любого j. Полное множество jk; j-k е z> есть ортонормиронанный базис для г² с ах

Дополнительное упрощение, введенное Малла гюз позволяет вычислять коэффициенты разложения исследуемой функции, используя дискретные фильтры ь^ и дп. Фильтр ь^ можно получцгъ из вложенности подпространств v^ < v$ и того, что ф_1т1 ортонормированный базис подпространства v •   ^ = ^hr^-m’ отсюда ьп= сф, Ф_1п>- Ортонормирюванность масштабных функций налагает на ь^ условие: Е hnhn+zk = 6ko <-^ко“СИМвол Кронекерат. Другой фильтр gn связан с вейвлет-функцией v и вытекает из вложенности подпространств wo с v_4: у- = Е оп<1п- причем существует простая связь между ьп и gr): дг=с-оп н_ ^$ или иногда дг = C-lDn h__,+1+ZN С ПОДХОДЯЩИМ выбором N е Z

Анализ с переменным иерархической схеме для исследуемой функции f я or разрешением вычисления

приводит к быстрой вейвлет-коэффициентов

г.у >

С 1 о~>

Начиная и коэффициентов разложения с® исследуемого сигнала для самого мелкого масштаба с самого высокого разрешения) легко получить! используя со:-, коэффициенты с' cj - 1,2,3 . >, а по формулам ао и вейвлеткоэффициенты ^ cj - 0,1,2. . ,э. Алгсригм можно рассматривать как вычисление последовательно огрубляемых аппроксимаций г. определяемых коэффициентами с', с однс^ременчым учетом информации, теряемой при переходе к более кртггу масштабу. Эта информация и отражается в вейвлет-козффщц^внтах d^. На практике наименьший возможный масштаб ощюделяв-'ця числом дискретных значении i анализируемого сигнала ¹ удобно, чтобы I = гЛ j е Z). При переходе от данно е масштаба к следующему число вейыет- коэффициентов уменьшается в два раза и процесс останавливается после конечного числа уровней. Так как масштабная функция хорошо локализована в пространство, тс в качестве коэффициентов г" = <г,ф ) можно взять сами дцекрэ' ные значения исходной функции.

В терминах функциональных пространств этот алгоритм соответствует разложению пространства v на сумму ортогональных подпространств   вейвлет-функций   последовзт^л; нс   огрубляемых масштабов; v = w » w е. . . ® w ®w ev . О О 1            J-l ., J

Хотя условия с 4-е? кажутся весьма сложными, аро^ложек' достаточно большое число функций, удовлетворлюших чрюбованиям анализа с не-именным разрешением, например, вейаяеты Мэйера, имеющие охрзничен.чый спектр в фу ръе-пространстве, вейвлеты Баттл-Лемари. основанные на сплайн-функциях, и вейвлеты Цобеши is) - гладкие функции отличные от нуля лишь нэ конечна« интервале, поэтому соответствующие им фильтры ь и о имеют конечное число ненулевых членов. Приведем значения коэффициентов фильтров для функции Хаара; ь = ь = г'1/2. и для функции Добеши 3-ГО порядка: h = 0.33267065, h = 0.80699151, h = 0.45967750. h = -0.13501102, h = -0.08544127, h = 0.03522629.

5 4 5

ВЕЙВЛЕТ-ПАКЕТЫ. Описанный выше алгоритм оставляет отк^пъм вопрос выбора самого базиса, ответ на который обычно не однозначен и зависит от характера исследуемого сигнала. При анализе аэрометрической информации весьма перспективным может оказаться использование предложенного недавно Викерхаузером из? метода вейвлет--пакетов. Пакеты расширяют класс базисных функций и предоставляют¹ целые "библотеюг базисов, которые подстраивают-он под конкретные масштабные и частотные особенности анализируе-■ ого сигнала. Грубо говоря, вейвлет-пакет есть множество функция из пространства l^zcrd с модулированными колебаниями, хорошо .локализованных как в пространстве, так и по частоте. С каждой функцией можно связать три параметра: масштаб, местоположение и частоту. Семейство вейвлет-пакетов получается посредством растяжения, переноса и модул? ¹ материнского" вейвлета.

Построение пакетов можно осуществить с использованием тех же дискретных фильтров ь и д. с помощью которых выполняется анализ с переменным разрешением. Определим последовательность функций:

$ ex? - а^1/2У мсгх - р 2т>                 Д j j п

СИ J

CxD

$_о<>^ можно отождествить с масштабной функцией Ф- а ф схз - с вейклет-функцией у- Определим функциональное пространство

О - < Г: Г = Г« $ Сх - j), w е R>. г>                              ***.! j n                              J

Тогда множество функций $nCx-.p, j t z является ортонормирован-ным базисом пространства пп Доказано пз), что функции s .

n е z, п > о образуют ортонормированный базис Аю Далее, введем пространство ^А- получаемое масштабным преобразованием

6^ = 2кХ2$пС2кх - j).

со е Р>.

Множество функций <гкХ2$г<г'х - jo. j е z> образует вейвлет-пакет. Из этого пакета функций можно выделить большое число различных ортонормированных базисов пространства Аю. Например, если взять в качестве' исходной функцию Хаара, то вейвлет-пакет будут образовывать функции Уолша различного порядка. Вейвлет-базис является частным случаем вейвлет-пакет базисов. Соответствующая ему последовательность подпространств имеет вид:

D е О е 6Q е. . . е 6kQ е. . . 011   1

Пусть г = fcx) - функция из пространства lArd и<г • Р е z> коэффициенты проекции г на пространство s^Ln самого мелкого масштаба.- г = сг ,2^L/Z^_oc2’'x - р». Тогда вводя обозначения A^k=cf ,2^k/2$_nC2^kx-p)) ,р е Z, О < k < L, О < п < 2^Ь*^к , ПОЛучаеМ реккурентные соотношения:

с 1 si

j

<14?

Используя эти соотношения легко получить все. возможные коэффициенты Ak, р е- z - соответствует положению базисной функции.

о г k < г - масштабу с отметим, что здесь большим к соответствуют малые масштабы.'-. о s п <, г*''^к - частоте. Коэффициеты разложения удобно представить в виде векторов <гр р с z>, организованных в бинарное .дерево. Корню дерева соответствует пространство ^^L0 а потомкам i.-k -го поколения ■ пидпрострап -^гва ^^г“_п. >■> -= о. . , е^1,4-1. Алгоритм вычисления векторов коэффициентов можно рассматривать как построение дерева начиная от корня: коэффициенты следующего уровня получаются из преждущег) путем применения соотношений ci3) и li4o. Ниже приведена схема элей процедуры для восьмиточечного сигнала: одинарная вертикальная линия обозначает применение фильтра в t формула i зэ, а двойная вертикальная линия - фильтра g <14э. Для примера выделены двойной рамкой коэффициенты. соответствующие вейвлет-базису.

Из данного вейвлет-пакета можно выделить очень большое число оргонормированных вейвлет-базисов. Нужно из этого множества базисов выделить наиболее подходящий для разложения данного сигнала. Например, Викерхаузер ггз) предложил быстрый алгоритм поиска базиса, минимизирующего некоторую ценовую функцию коэффициентов, например информационную энтропию. С практической точки зрения такой базис минимизирует число существенных коэффициентов ст.е. коэффициентов, которые превосходят некоторое пороговое значение). Базисные функции, соответствующие этим коэффициентам, содержат почти всю информацию о сигнале и могут позволить выделить его характерные моды.

Первый этап этого алгоритма состоит в вычислении ценовой функции для всех узлов дерева. Затем, проходя дерево снизу вверх, отбрасываем нижележащие ветви, если значение ценовой Функции отца меньше суммы ценовых функций сыновей Тогда для данного сигнала и ценовой функции получается вполне определенный ортонормированный базис.

Для сигнала, представленного в виде т - гк дискретных значений, алгоритм !,жерхаузера ищет оптимальный базис из множества, содержащего г1 различных ортонормированных базисов. Однако этот алгоритм определяет далеко не все возможные базисы, но эффективный способ просматривания полного множества неизвестен. Кроме того, оптимальный базис с точки зрения минимума энтропии не всегда является подходящим для выделения конкретных особенностей сигнала. Например, хорошо идентифицируя главные гармоники сигнала . такой базис может "игнорировать" мелкомасштабную структуру сигнала. Эту проблему можно решать введением .некоторых эмпирических требований на вид базиса, например ограничивать максимальный используемый масштаб. дли варьировать длину анализируемого сегмента сигнала.

НЕКОТОРЫЕ Ш^ИМЕРЫ. Объем статьи позволяет продемонстрировать возможности вейвлет анализа лишь на нескольких характерных примерах. Первый пример не имеет отношения к аэрометрическим данным, но хорошо демонстрирует возможности подхода с рис.ал. Сигнал представляет собой сумму двух периодических составляющих, каждая с линейно меняющейся частотой. В нижней части рисунка приведен сам сигнал, верхняя часть - фазовая плоскость время-частота. Отметим. что наглядное представление результатов вейвлет-преобразования валяется самостоятельной проблемой. В нашем случае при построении рисунков фазовая плоскость разбивается на прямоугольники

Второй пример ближе к проблемам экологии и соответствует сигналу, включающему две гармонические компоненты и три случайных выброса срис.эо. Причем, если два из них хорошо видны на графике самой функции, то третий, имеющий такую же амплитуду, почти не заметен. 3 поле вейвлет-представлэния постоянной частоте соответствует горизонтальная периодическая структура, а локальному выбросу - вертикальная. К сожалению, качество печати не позволяет передать видимую на экране дисплея мелкомасштабную структуру рисунка.

Третий пример касается суточной изменчивости концентраций примеси в атмосфере. Известно и.аз, что для окиси углерода почти во все сезоны наблюдаются два вида суточной изменчивости, либо с одним, либо с двумя максимумами. Сигнал на рис.4 сформирован из фрагментов, точно соответсуюших этим двум типам изменчивости, взятым из ш, плавно сменяющих друг друга. Задача состоит в разделении интервал-' времени, в которые доминирует тот или иной тип зависимостей.

Приведенные примеры лишь иллюстрируют возможности подхода. Остается много проблем как общего плана, связанных с выбором базиса, оптимизацией алгоритмов, представлением результатов, так и специфических, возникающих при работе с аэрометрическими данными. К последним относится в первую очередь проблема пробелов в выборках - замеры на постах наблюдения проводятся, как правило, три раза в сутки, в 7, 13 и 19 часов и не проводится в ночное время, а также в выходные и праздничные дни. В то же время именно этот аппарат дает надежду на выделение из достаточно сложных временных последовательностей данных Это могут быть как отдельные метеопараметры или концентрации примесей, так и интегральные показатели состояния атмосферы характерных временных структур с целью их использования для дальнейшего прогноза состояния системы.

Рис. 2

Рис. 3

Чвее;?*

*6е« jfe ■»■>£!#

AWWMMAAAAAAAAAAWWWM^

Рис. 4