Применение вейвлет-преобразования для слияния многоспектральных изображений

Комплексные многосенсорные системы наблюдения и обнаружения целей получили в настоящее время широкое распространение, прежде всего из-за способности работать в условиях сильных помех естественного и искусственного происхождения. Каждый отдельно взятый канал не в состоянии удовлетворить техническим требованиям в условиях плохой видимости, маскировки целей и применения средств радиоэлектронного противодействия. Однако эффективность системы увеличивается за счёт совместного использования информации, получаемой от различных каналов. Обычно в состав оптико-электронной аппаратуры включаются телевизионный, тепловизионный (в нескольких диапазонах), лазерный и другие каналы [1, 2].

Слияние информации из разных каналов может выполняться на различных уровнях: слияние на уровне решений, слияние признаков, слияние данных. Слияние на уровне данных часто называется слиянием низкого уровня. Оно больше всего применимо для интеграции данных от датчиков с совместимым темпом получения, размерностью и форматами данных. В свою очередь, алгоритмы слияния данных можно разделить на две группы: формирующие псевдоцветные изображения и формирующие изображения в натуральных цветах. Псевдоцветные изображения по большей части используются при обработке данных дистанционного зондирования Земли и в медицинских приложениях [3,4].

В данной работе рассматривается слияние изображений одной и той же сцены, полученных в разных спектральных диапазонах, с формированием интегрированного монохромного изображения.

Главной проблемой компиляции изображений для визуального отображения является «сохранение рисунка» [5]: на результирующем изображении должны быть представлены важные детали из всех объединяемых изображений, а сама процедура компиляции не должна вносить искажений. Визуальное качество компилированного изображения должно быть, по крайней мере, не хуже качества исходного изображения при блокировании остальных каналов наблюдения. Метод компиляции должен обеспечивать работу с любым количеством каналов наблюдения, независимо от их спектрального диапазона и сочетания.

Ранние алгоритмы компиляции монохромных изображений были основаны на взвешенном суммировании исходных изображений с некоторыми весовыми коэффициентами. Объединение существенных деталей сводилось к добавлению в эту линейную комбинацию максимальных контрастов из всех каналов [6].

Более поздние алгоритмы основаны на выделении тем или иным методом яркостных перепадов в каждом из исходных изображений и объединении их в интегрированном изображении. При объединении изображений разных спектральных диапазонов хорошие результаты были получены при анализе спектра Фурье [5]. Также известны алгоритмы компиляции, основанные на многомасштабном разложении, включающем различные пирамидальные алгоритмы (например, пирамиды Лапласа), контурлет-преобра-зование [7], курвлет-преобразование и дискретное вейвлет-преобразование [8–11]. Вейвлет-преобразование, в отличие от преобразования Фурье, позволяет проводить локальный спектральный анализ. Спектральные вейвлет-коэффициенты соответствуют не только амплитудам различных частот, но и различным пространственным участкам на изображении. К достоинствам вейвлет-анализа также стоит отнести возможность использования для комплексирования изображений разного пространственного разрешения, что уменьшает объём обрабатываемой информации.

Ещё одно направление компиляции на основе многомасштабного разложения - представление исходного изображения в виде совокупности пространственно-ориентированных деревьев, составленных из коэффициентов вейвлет-разложения [12]. Такое представление позволяет комплексировать зашумлённые изображения без пороговой обработки вейвлет-коэффициентов [13].

Методы компиляции на основе вейвлет-анализа

Методы компиляции на основе вейвлет-анализа описаны в [6, 9, 10]. В качестве базиса в этих работах выбрана система вейвлетов Хаара, требующая минимума вычислений. Используется разделимый двумерный базис, получаемый с помощью целых сдвигов и двоичных изменений масштаба одномерных функций.

Двумерная масштабирующая функция p ( x , у ) и три двумерные вейвлет-функции ф H ( x , у ), ф V ( x , у ), ф D ( x , у ) формируются из произведений одномерных масштабирующих функций p ( x ), р ( у ) и вейвлет-функций ф ( x ), ф ( у ):

ф ( x , у ) = ф ( x ) ф ( у ), ф ^H ( x , у ) = ф ( x ) ф ( у ), ф V ( x , у ) = ф ( x ) ф ( у ), ф D ( x , у ) = ф ( x ) ф ( у ).

Двумерные вейвлет-функции чувствительны к изменениям яркости изображения в разных направлениях: ф ^H ( x , у ) чувствительна к перепадам вдоль столбцов, которые соответствуют горизонтальным краям объектов, ф V ( x , у ) чувствительна к перепадам вдоль строк, а ф D ( x , у ) - вдоль диагоналей.

Объединяемые изображения подвергаются двумерному дискретному вейвлет-разложению: каждая строка делится на низкочастотную и высокочастотную половины, далее аналогично обрабатывается каждый столбец. В результате получаются матрицы вейвлет-коэффициентов, т.е. четыре изображения половинного размера от исходного: к p - низкочастотное по горизонтали и вертикали (НЧНЧ), W V - низкочастотное по горизонтали и высокочастотное по вертикали (НЧВЧ), W^H - высокочастотное по горизонтали и низкочастотное по вертикали (ВЧНЧ), W D - высокочастотное по горизонтали и вертикали (ВЧВЧ).

После формирования матриц вейвлет-коэффи-циентов сформировать единое изображение можно несколькими способами. Значения коэффициентов НЧНЧ части вейвлет-спектра могут поступать из одного канала (заранее выбранного) или могут собираться как среднее или взвешенное среднее по всем каналам. Собирая матрицы коэффициентов высоко- частотных частей спектра, можно сравнить соответствующие коэффициенты из каждого канала и выбрать коэффициент с максимальным абсолютным значением. Также высокочастотные коэффициенты могут выбираться на основе некоторого признака. В любом случае перед обработкой необходимо выполнять нормализацию. Изображения, поступающие от всех датчиков, должны иметь одинаковый диапазон яркостей.

Наиболее простой способ слияния описан в работах [6, 8, 10–11]. Авторы формировали низкочастотные коэффициенты к p как среднее по двум каналам, а матрицы W ^V , W ^H и W ^D собирали, выбирая из пар вейвлет-коэффициентов максимальный по модулю.

В работе [9] авторы проверяют корреляцию коэффициентов НЧНЧ части для изображений разных каналов. Для каждой точки ( m , n ) рассматривается окрестность S m,n , размер окрестности авторы выбирали 3 x 3 и 5 x 5. По этой окрестности рассчитывается локальная энергия s ( m , n ) и аналог коэффициента нормированной корреляции С ( m , n ):

2 Е Е к ф1 ( k , l W k , l )

C (m, n) = (k ,1 )e Smn----------------------------, s1( m, n) + s2( m, n)                     (2)

^{s ( m} , ⁿ ) = Е Е W ^{( k} , ¹ k

(k, 1 )e Smn где кpi, кp2 - коэффициенты НЧНЧ части для изображений из первого и второго канала.

Полученный коэффициент С (m, n) сравнивается с заранее заданным порогом T, авторы [9] рассматривают порог в интервале (0,5, 1). Если С(m, n) < T, то вейвлет-коэффициент объединенного изображения рассчитывается по следующей формуле кф (m, n)

кф1( m, n), кф2(m, n),

if s 1 ( m , n ) > s ₂( m , n ), otherwise .

Если С ( m , n )> T , то вейвлет-коэффициент представляет собой линейную комбинацию коэффициентов из двух каналов:

к ф ( m , n ) = to i к _H ( m , n ) + ® 2 к ф2 ( m , n ),

, Ito max , to 1 + to ₂ = 1, to 1 = < l® min ,

if si(m, n) > S2 (m, n), (4) otherwise, tomin

1   1 - C ( m , n )

2 2(1 - T) , tomax    1   tomin .

Следует отметить, что слияние на основе анализа корреляции коэффициентов по формулам (2–4) применяется не только для НЧНЧ части спектра, но и для высокочастотных вейвлет-коэффициентов [14].

Поскольку высокочастотная составляющая содержит подробную информацию о границах объектов и значения высокочастотных коэффициентов в пределах окрестности могут существенно отличаться, то для формирования W V, W H и W D в [9] используется стратегия слияния на основе дисперсии, рассчитанной по локальной окрестности. Авторы [9] использовали размер окрестности от 3x3 до 7x7. Для каждой из частей НЧВЧ, ВЧНЧ и ВЧВЧ в локальной окрестности каждой точки (m, n) вычисляется весовой коэффициент слияния:

T v ⁱ ar ( m , n )

2 d 1 ⁱ d 2 ⁱ

( d 1 ) 2 + ( d 2 )²

где d 1 , d 2 – дисперсия значений вейвлет-коэффициен-тов в локальной окрестности точки ( m , n ) для первого и второго изображения, верхний индекс показывает, для какой части спектра выполняются вычисления, = H , V , D.

Если коэффициент слияния T var больше заранее заданного порога t , то вейвлет-коэффициент вычисляется как линейная комбинация коэффициентов из двух каналов, в противном случае он выбирается из канала с максимальной дисперсией:

w i W^(m , n ) + w i W 2 ( m , n ), T ar ^ t¹ ,

W^l ( m , n ) = <

W i ( m , n ), if d i >  d 2 , T var <  t i ,

W 2 (m , n),ifd 1 <  d 2, T Var <  t,

wi = dd! (Vdr + dd)), wl + w2 = 1, где Wl - высокочастотные коэффициенты объединенного изображения, Wi, W2 - высокочастотные коэффициенты для изображений из первого и второго канала, = H, V, D.

Описанные алгоритмы были промоделированы на тестовых и реальных изображениях. Результаты моделирования показали, что при выборе максимальных по модулю высокочастотных коэффициентов [8] на синтезированное изображение попадает слишком много мелких деталей, что затрудняет его анализ. Особенно критичным подход выбора по максимуму становится при зашумлении одного из изображений, так как синтезированное изображение оказывается искажено шумами.

Метод слияния высокочастотных компонент на основе анализа дисперсии значений вейвлет-коэффи-циентов по формулам (5, 6) даёт хорошие результаты, но требует задания пороговых значений, с которыми сравниваются весовые коэффициенты слияния T var . При моделировании пороговые значения рассчитывались при предварительном проходе по изображению. Таким образом, процедура слияния становилась двухпроходной. При зашумлении одного из изображений результаты слияния оказались близкими к методу выбора по максимуму. Это объясняется тем, что при больших значениях дисперсии в областях с шумом и, следовательно, малых значениях T var вейвлет-коэффициенты выбираются из канала с максимальной дисперсией.

На рис. 1 показан пример тестового изображения и изображения, искажённого Гауссовым шумом. На рис. 2 приведены результаты слияния этих изображений. Коэффициенты НЧНЧ части выбираются из исходного тестового изображения (рис. 1 а ). На рис. 2 а показан результат слияния при выборе максимальных по модулю высокочастотных коэффициентов, на рис. 2 б – результат слияния по формулам (5, 6), размер окрестностей для расчёта дисперсии - 5 x 5. Принципиальных различий между изображениями, синтезированными этими двумя методами, нет. Зашумлёнными оказываются не только области постоянной яркости и плавно изменяющейся яркости (серый клин), но и структурированные области (шахматная доска и горизонтальные полосы).

Рассмотренные методы слияния позволяют объединять изображения из разных каналов, однако они не устойчивы к шуму. Требуется разработать новый подход, который бы, наряду с объединением существенных деталей входных изображений, обеспечивал фильтрацию помех.

Рис. 1. Исходное и зашумлённое изображения

в)

Рис. 2. Результаты слияния: методом максимальных значений (а), методом расчёта коэффициентов T var (б), методом расчёта коэффициентов анизотропии (в)

Метод слияния высокочастотных коэффициентов

Для двумерного дискретного вейвлет-разложения на базисе вейвлетов Хаара рассмотрим новый метод слияния высокочастотных коэффициентов, не требующий задания пороговых значений.

Обратим внимание на то, что двумерные функции Ф ( x , y ), v H ( x , У ), V V ( x , У ) и V D ( x , У ) совпадают с матрицами 2 x 2 двумерного дискретного преобразования Фурье:

- j 2n ( k -0+ 1 -0) e ^N

- j 2 ^П ( k -0+ 1 -( N -1)) e ^N

F_k i = — k , l N

- j 2П ( k -1+ 1 -0) e ^N

-j^ ( k + 1 )-( N -1) e ^N

где k , l = 0 + N -1, j ²=-1.

При N =2

^F k ’ l = 2

cos п ( k ■ 0 + 1 ■ 0) cos п ( k - 1 + 1 • 0)

cos п ( k ■ 0 + 1 - 1) cos п ( k - 1 + 1 - 1)

k , l = 0 - 1,                                             (7)

Ф ( x , У ) = F ),0 , V V ( x , У ) = F m ,

V ^H ( x , У ) = F 1,0 , v D ( x , У ) = F_v .

Если фрагмент изображения содержит контуры объектов, то спектр Фурье этого фрагмента будет анизотропным. В направлении, взятом вдоль прямоугольного контура, энергия спектра Фурье существенно ниже, чем в перпендикулярном направлении, т.е. в направлении градиента яркости.

В [5] вводится степень анизотропии фрагмента на основе анализа дискретного двумерного спектра Фурье фрагментов размером от 3 x 3. Энергия спектра рассчитывается в четырёх направлениях, составляющих углы 0, п /4, п /2, 3 п /4 с горизонталью. Направление, в котором будет получена максимальная суммарная энергия, принимается за ориентацию градиента яркости. Формула для расчёта степени анизотропии имеет следующий вид:

A = En-

E m ,

где E m , E n - суммы элементов энергетического спектра Фурье в направлении с максимальной энергией и в перпендикулярном направлении соответственно.

Но в спектре фрагмента размером 2 x 2 для диагонального направления нельзя найти перпендикулярное. Энергию в диагональном направлении можно сравнивать только с энергией по вертикали и горизонтали. Поэтому, возвращаясь к терминологии вейвлет-преобразования, введём коэффициенты анизотропии в горизонтальном A^H , вертикальном A^V и диагональном A^D направлениях:

A ^H =

W ^V

W ^H

A ^V

W ^H

W ^V

, A D =

max (I W H\ , W ^V I) ,9)

_WD . ()

В отличие от степени анизотропии (9), коэффициенты анизотропии по направлениям могут быть больше 1, что говорит об отсутствии перепада яркости в данном направлении. Для шумовых фрагментов значения коэффициентов анизотропии будут близки

к 1. Чем меньше значение коэффициента анизотропии, тем существеннее перепад яркости в данном направлении. Исключением служат идеальные ступенчатые перепады в направлениях п /4 и 3 п /4, когда все три высокочастотных вейвлет-коэффициента имеют одинаковые абсолютные значения и коэффициенты анизотропии будут равны 1. Чтобы избежать деления на 0, в формуле (9) к знаменателю следует прибавлять малую константу (машинную точность).

Введём правило слияния высокочастотных вейвлет-коэффициентов, используя коэффициенты анизотропии по направлениям:

W i , if A i <  A 2 , A i <  1,

W i =^

W 2 , if A 2 <  A i , A 2 <  1,

W_a ⁱ , otherwise,

i = H , V , D ,

где a = arg min (| W i |, | W ₂ i |) .

На рис. 2 в приведены результаты слияния тестового и зашумлённого изображений (рис. 1) предложенным методом по формуле (10). Зашумлёнными оказываются области плавно изменяющейся яркости, кроме того, присутствуют искажения на границах объектов (зашумляется область постоянной яркости, примыкающая к объектам). На структурированных областях по сравнению с рис. 2 а и рис. 2 б шумов существенно меньше.

Для проверки устойчивости методов слияния к шуму рассматривался набор исходных реальных изображений, разделённых на фрагменты. Анализируются три группы фрагментов. Фрагменты первой группы не содержат визуально значимых перепадов яркости, фрагменты второй группы содержат перепады с малой амплитудой (меньше средней амплитуды по всему изображению), а фрагменты третьей группы - перепады с большой амплитудой. Изображения искажаются аддитивным Гауссовым шумом, пиковое отношение сигнал / шум равно 23. Выполнялось слияние исходных изображений с искажёнными копиями. Коэффициенты НЧНЧ выбирались из исходных изображений. Высокочастотные коэффициенты выбирались как максимальные по модулю, по формулам (5), (6) и предложенным методом по формуле (10).

Для всех результатов слияния были рассчитаны коэффициенты корреляции с исходным изображением. Общее количество фрагментов в эксперименте - по 50 в каждой группе. Примеры полученных значений коэффициентов корреляции ( K ) приведены на рис. 3. По оси абсцисс откладываются значения среднеквадратичного отклонения яркости фрагмента. По оси ординат - значения коэффициентов корреляции исходного изображения с зашумлённой копией и с синтезированными изображениями.

Все три метода слияния дают результат более близкий к исходному изображению, чем искажённая копия. Однако коэффициенты корреляции с синтези-

рованными изображениями, полученными предложенным методом, выше, чем у аналогов. Кроме того, прослеживается зависимость результатов слияния от амплитуды перепадов яркости. Для фрагментов третьей группы корреляция синтезированных изображений с исходными выше, чем для первой и второй

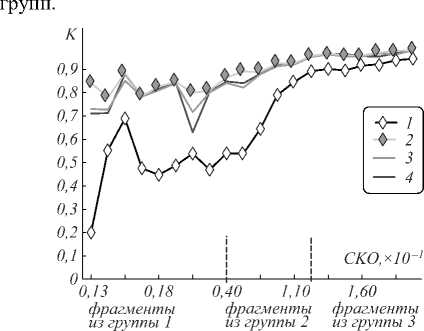
Рис. 3. Коэффициенты корреляции с исходным изображением зашумлённой копии (1) и результатов слияния методом расчёта коэффициентов анизотропии (2), методом максимальных значений (3), методом расчёта коэффициентов T var (4)

Как отмечено в [12], слияние максимальных по модулю высокочастотных коэффициентов хорошо работает с относительно качественными (слабо искажёнными) изображениями. В случае комплексирова-ния зашумлённых изображений необходимо предусматривать дополнительные средства шумоподавления. В предложенном методе таким средством является проверка на анизотропию. Значения высокочастотных коэффициентов в спектре зашумлённого изображения могут быть больше, чем в спектре исходного, однако случайные шумы снижают анизотропию. Высокий коэффициент корреляции синтезированного изображения с исходным говорит о том, что большее число высокочастотных коэффициентов поступает именно из неискажённого изображения. Таким образом, рассмотренный метод является более устойчивым к зашумлению входных изображений по сравнению с аналогами.

Слияние низкочастотных коэффициентов

Формирование коэффициентов НЧНЧ части вейвлет-спектра как линейной комбинации коэффициентов из разных каналов весьма популярно. Но этот метод приводит к потере контраста ярких деталей, особенно при слиянии телевизионного и тепловизионного изображений. Было проведено моделирование слияния по формуле (4), как описано в работе [9]. Однако при использовании этого подхода с возможностью выбора максимальных коэффициентов НЧНЧ части спектра при объединении телевизионного и тепловизионного изображений были получены артефакты в виде светлых пятен, нарушающие «рисунок» синтезированного изображения.

Для слияния коэффициентов НЧНЧ части рассмотрим способ, предложенный для объединения полутоновых изображений [15].

Первоначально требуется определить наиболее информативный канал (например, с максимальной дисперсией яркости), коэффициенты НЧНЧ части спектра из этого канала обозначим W ϕ1 . Коэффициенты НЧНЧ из второго канала обозначим W ϕ2 .

Затем вычисляются абсолютные разности между значениями коэффициентов НЧНЧ части из второго канала и средним значением этих коэффициентов, назовём эти разности контрастом:

Δ W φ2 ( m , n ) = W φ2 ( m , n ) - W φ2 ,

₁ MN                           (11)

Wφ2=MN∑m=1∑n=1Wφ2(m,n), где M ×N - размер матриц коэффициентов НЧНЧ. Средний контраст вычисляется по формуле

1 MN

W Δφ2 = ∑∑ Δ W φ2 ( m , n ).

MN m =1 n =1

Низкочастотные коэффициенты объединённого изображения рассчитываются как

W φ ( m , n ) = W φ1 ( m , n ) +Δ W φ2 ( m , n ) - W Δφ2 . (13)

Иными словами, в каждой точке к значению коэффициента НЧНЧ части из основного канала добавляется (или вычитается) отклонение от среднего контраста из второго канала. Данный метод зависит от порядка входных изображений, но он позволяет сохранять контраст деталей на объединённом изображении. Особо стоит отметить, что перед слиянием изображения должны быть приведены не только к одинаковому диапазону изменения значений яркости, но и к одинаковому среднему значению.

На рис. 4 представлены исходные разносюжетные изображения, а на рис. 5 - результаты слияния. Рис. 5 а соответствует порядку рис. 4 а , рис. 4 б . Рис. 5 б соответствует порядку рис. 4 б , рис. 4 а . Высокочастотные коэффициенты формировались по формуле (10). Для сравнения на рис. 5 в приведён результат слияния при формировании коэффициентов приближения как среднего из двух каналов. Легко заметить, что при суммировании теряется контраст ярких деталей и роза и «пузырьки» выглядят блеклыми, а при слиянии по формуле (13) контраст сохранён.

Слияние произвольного количества изображений

Рассмотренные методы слияния вейвлет-коэф-фициентов могут быть легко модифицированы для слияния произвольного количества изображений. Для этого в формуле (10) вместо сравнения коэффициен- тов анизотропии по направлениям из двух каналов нужно искать минимальный коэффициент по всем каналам:

\ W k , if k = argmin A l , A <  1,

W i = J                    i =i₊ L                            (14)

\_Wa , otherwise, где a = arg min | W, |, неразличимые в одном из диапазонов. Для удобства анализа на рис. 6 такие фрагменты выделены рамками. Синтезированные изображения выглядят более чёткими. Использование двух уровней разложения позволяет существенно уменьшить время на обработку. Однако увеличение числа уровней разложения может быть оправдано при слиянии изображений с крупными деталями или объектами. На изображениях с мелкими объектами появляется эффект мозаики, а плавные границы становятся ступенчатыми.

L - число каналов, i = H , V , D .

а)

Рис. 4. Исходные изображения

б)

a)

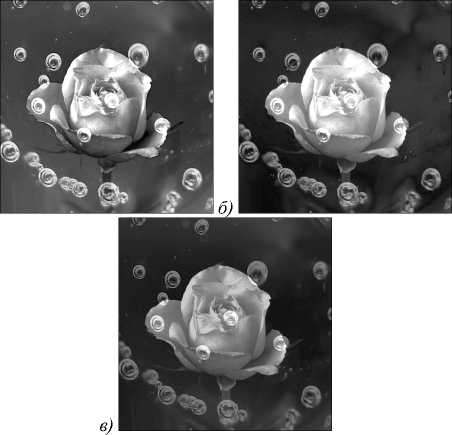
Рис. 5. Результаты слияния: с учётом контраста по формуле (13) (а, б), – методом усреднения (в)

Для слияния низкочастотных коэффициентов в формуле (13) добавляем контраст из всех каналов:

в)

а)

Рис. 6. Слияние трёх изображений: исходные изображения (а , б , в), результат слияния, один уровень вейвлет-разложения (г)

Рис. 7. Результат слияния, два уровня вейвлет-разложения

Заключение

W ф ( m , n ) = W ^.1 ( m , n ) + ^ ( A W ф i ( m , n ) - W _Дф i ) .    (15)

l =2 ^X

Пример слияния трёх спектрозональных изображений приведён на рис. 6. За первое входное взято изображение, приведённое на рис. 6 а , порядок остальных изображений не имеет значения. Слияние предложенным методом может проводиться на любом уровне вейвлет-разложения. На рис. 7 показан результат слияния при разложении на два уровня.

Полученные результаты показывают, что на результирующем изображении присутствуют детали,

Результирующие изображения, полученные при слиянии по рассмотренному алгоритму, удобны для восприятия оператором. Алгоритм не вносит дополнительных искажений и собирает всю необходимую информацию с исходных изображений. Процедура слияния не требует введения каких-либо пороговых значений. Предложенный алгоритм может быть использован в оптико-электронных системах автоматической обработки изображений.

В данной работе не рассматривалась возможность дополнительного улучшения качества формируемых изображений, в частности за счёт направленной фильтрации при вейвлет-разложении. Дальнейшие исследо- вания направлены на адаптацию алгоритма слияния с параллельным улучшением качества результата.