Применение высокомодульных керамических композиционных материалов для перспективных оптоэлектронных устройств

Детали современных оптоэлектронных устройств относятся к наиболее точным изделиям прецизионного приборостроения. Одним из главных критериев качества такой детали является сохранение точности ее геометрической формы при гравитационных и термических воздействиях [1]. При работе изделий в условиях динамических нагрузок, важное значение для точности имеют также вибрационные свойства деталей, зависящие во многом от их жесткости и плотности материала, определяющих в конечном итоге значения собственных частот колебаний f . В настоящее время совершенствование большинства технических систем, имеющих в конструкции оптоэлек- тронные устройства, ведётся по пути уменьшения массогабаритных характеристик за счёт использования высокомодульных материалов, обладающих при этом относительно малой плотностью.

Способность материала сохранять форму детали под действием динамически изменяющихся внешних сил (вибростойкость) определяется удельной жесткостью – отношением модуля упругости материала к его плотности ( ^/p ). С увеличением этого отношения растет частота собственных колебаний f~ E/p – вибростойкость увеличивается. Свойства некоторых материалов, отвечающих высоким требованиям вибростойкости представлены в табл.1.

Из таблицы видно, что наибольшую удельную жесткость имеет бериллий, значительно превосходящий другие металлы. Наибольшей устойчивостью формы под воздействием тепловых потоков обладает кремний. Безусловным «лидером» по всем показателям является алмаз, механические и теплофизические свойств которого во много раз превышают свойства других материалов. Однако использование алмаза как конструкционного материала сегодня не представляется реальным в основном из-за особенностей его физико-химических свойств, ограничивающих изготовление из него деталей больших размеров и сложных форм.

Перспективным направлением для решения проблемы создания вибростой-ких деталей современных оптоэлектронных устройств является применение высокомодульных керамических композиционных материалов, например, полученных за счет армирования карбидо-кремниевой керамики алмазными зернами [3].

Таблица 1. Свойства материалов [2].

Материал	Е , ГПа	ρ, кг/м3	Е / ρ g , 106м
Al	69	2700	2,7
Cu	115	8900	1,3
W	420	19350	2,2
Si	157	2300	6,8
Be	280	1850	15,1
SiC	400	3050	13,0
Алмаз	1100	3510	31,3

Известно [2], что карбидокремни-евая керамика, получаемая методом реакционного спекания, содержит в своем составе карбид кремния и свободный (элементарный) кремний. Поэтому армирование керамик будет приводить к образованию трехфазного материала, состоящего из алмаза, карбида кремния и кремния.

На первом этапе была разработана реологическая модель прогнозирования модуля упругости [3] керамического материала алмаз – карбид кремния – кремний. Реологическая модель материала представлена структурой в виде изолированных сфер алмаза, окруженных сферическим слоем карбида кремния SiC. Оставшийся объем заполнен кремнием (рис.1). Такое структурное представление материала в большой степени соответствует реальной микроструктуре композита (рис. 2).

Рисунок 1. Структурное представление композита : алмаз – карбид кремния: алмаз – белый; карбид кремния – серый; кремний – черный

Рисунок 2. Микроструктура композита алмаз – карбид кремния

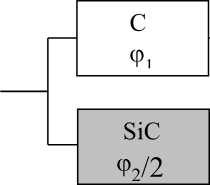
Выбранное структурное представление позволяет предложить реологическую модель, соответствующую, показанной на рис. 3. В этой модели учтены (с определенным уровнем допущений) параллельные и последовательные связи фаз материала, возникающие при механическом воздействии на материал. Дей- ствительно, условно выделенный вертикальный слой материала, включающий алмазные зерна, связанные карбидной матрицей, последовательно связан со слоем материала, состоящего из кремния, связанного карбидом кремния.

SiC 2 /2

Si

Рисунок 3. Реологическая модель композита алмаз – карбид кремния

Реологическая модель последовательно параллельных связей позволяет полить выражение для эффективного модуля упругости E, в зависимости от объ- емного содержания и упругих констант, входящих в материал фаз:

E

(ф 1 +92/2)2  ₍   (фз+ф2/2)²

1 E 1   2 E 2 2    3 E 3   2 E 2 2

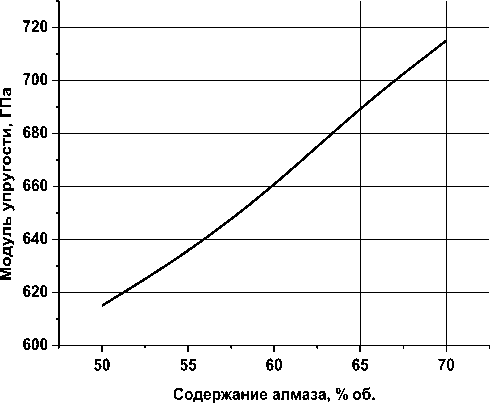
Рисунок 4. Расчетные значения модуля упругости композита от содержания в нем алмаза

На основании полученного соотношения (1) были рассчитаны значения модуля упругости композита с различным содержанием в нем компонентов. В расчете использовали следующие значения модулей упругости: алмаз – 1100

ГПа, карбид кремния – 400 ГПа, кремний – 110 ГПа.

Как показали расчеты большого числа составов композитов, модуль упругости всего композита зависит, в первую очередь от содержания в нём алмаза (рис.4).

Сделанные расчеты и выводы по ним легли в основу проведенных разработок составов и методов получения материалов и измерений их упругих характеристик.

Для проведения исследований упругих свойств композитов алмаз – карбид кремния была использована динамическая методика определения модуля упругости [2]. Сущность метода заключается в определении частот собственных колебаний образцов из композиционных материалов с помощью резонансного метода и вычислении модуля упругости по соотношениям, связывающим модуль упругости и частоту собственных колебаний.

Разработанная методика была использована на композитах алмаз – карбид кремния, приведенных в таблице 2. Композиты получали в форме пластин размером 85 х 9 х 4 мм [3]. Внешний вид изготовленных образцов приведен на рис. 5.

Рисунок 5. Образы композиционных материалов алмаз – карбид кремния с повы-

шенным содержанием алмаза, предназначенные для измерения модуля упругости

Из табл. 2 следует, что расчетные (по уравнению (1)) и экспериментальные значения модуля упругости материалов, имеющих различный компонентный состав, хорошо согласуются между собой, подтверждая тем самым возможность использования уравнения (1) для моделирования упругих свойств композитов алмаз – карбид кремния. Заметим, что расхождение между расчетными и экспериментальными величинами находятся в диапазоне 2 – 9%, при этом экспериментальные значения несколько выше (отклонение возрастает в большую сторону с увеличением алмазной фазы). Такие отклонения расчет/эксперимент вполне допустимы.

Таблица 2 . Модуль упругости (эксперимент) композиционных материалов алмаз – карбид кремния

Состав, % об.			о н о н о S	Модуль упругости, ГПа		^ ^ 7<
8 s ч <	у Й	Й		экспе пери-ри-мент	расчет
42	52	6	3,28	570	580	17,7
55	39	6	3,32	645	632	19,8
60	35	5	3,34	700	670	21,3
67	28	5	3,36	770	707	23,3
68	27	5	3,37	785	715	23,7

Как следует из таблицы, экспериментальные измерения подтверждают сделанные в ходе модельных расчетов выводы: увеличение содержания алмаза приводит к существенному повышению модуля упругости композитов. Получены композиционные материалы алмаз-карбид кремния – кремний с модулем упругости более 750 ГПа, что заметно превышает модуль упругости всех известных композиционных материалов.

Удельная жесткость композита алмаз – карбид кремния – кремний дости- гает 23.106 м, что на 50% больше чем у бериллия и на 80% больше чем у карби-докремниевой керамики.

Таким образом, композит алмаз – карбид кремния – кремний (АКК) имеет уникальные по уровню физикомеханические свойства, что позволяет рассчитывать на создание оптоэлектронных деталей из него с недостижимым ранее уровнем гравитационной стабильности.

Следующим этапом работы проведено численное исследование вибростойкости конструкций элементов оптоэлектронных устройств, выполненных с применением разработанного материала на основе модального анализа, реализованного в пакете программ Solid Works\СоmpasWorks. Конструкция в данном пакете программ представляется трехмерной расчетной областью, по отношению к которой проведена конечноэлементная дискретизация. Механические и физические свойства расчетной области в численном эксперименте соответствовали назначенным свойствам материала АКК.

Модальный анализ представляет собой расчетное средство для определения собственных частот и форм колебаний конструкции [4]. Модальный анализ здесь рассматриваются как решение задачи о свободных незатухающих колебаний

I K| — (02 M{U} = 0 ,           (2)

где: K и M - матрицы жесткости и масс системы;    (квадрат собственной частоты) - собственное значение, {U} (собственные формы, не являющиеся функциями времени) собственные формы колебаний.

При выполнении спектрального анализа программа определяет перемещения в конструкции для каждой формы колебаний. Как правило, наилучшей конструкцией, с точки зрения вибростойкости и точности для рассматриваемого случая будет та у которой, из всех возможных форм собственных колебаний частоты будут наибольшими. При этом нижние частоты, как правило, являются наиболее значимыми. Именно они будут определять частотные погрешности оптоэлектронных устройств, возникающие при динамическом воздействии внешних

На рис. 6 приведены варианты трех исследуемых конструкций проектируемого элемента оптоэлектронного устройства.

сил.

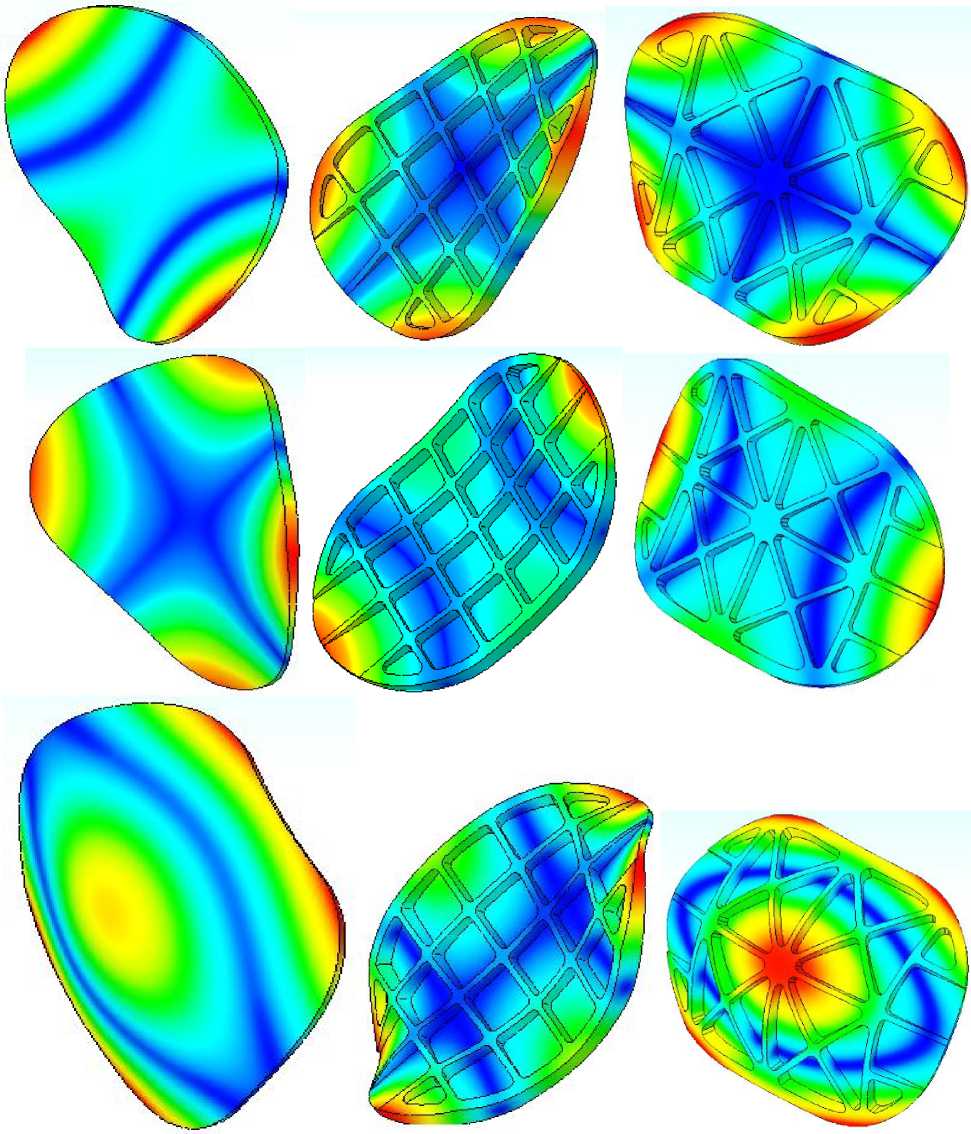
Рисунок 6. Варианты форм собственных колебаний (форм. 7 -10 ) трех исследуемых конструкций проектируемого элемента оптоэлектронного устройства

Таблица 3. Сопоставительный расчёт вариантов подложки из разных материалов

	1	2	2	3
Материал	АКК	АКК	SiC	SiC
Расчетные параметры , кг/см2 Е, ГПа	3,34 710	3,34 710	3,10 400	3,10 400
Результаты:
V, см3	386,1	355,1	355,1	414,9
m, кг	1,289	1,186	1,101	1,286
Момент инерции, кг/см2: Px Py Pz	37,847 68,016 105,732	40,326 64,423 104,382	37,428 59,794 96,882	40,326 64,423 104,382
.,Гц (максимальное перемещение, мм): форма 7 форма 8 форма 9 форма 10	1705 (2,067) 1727 (2,675) 3574 (1,888) 3853 (2,548)	1962 (2,061) 2230 (2,799) 3921 (1,631) 4305 (2,805)	1542 (2,131) 1746 (2,899) 3069 (1,693) 3379 (2,899)	1962 (2,061) 2230 (2,799) 3921 (1,631) 4305 (2,805)

Из расчетов следует, что собственные частоты зависят от свойств материала и от конструкции детали. В рассматриваемом случае наилучшие свойства будет иметь конструкция вар.3. выполненная из материала АКК.