Применение задач оптимизации в кластерном анализе

Кластеризация методом минимальных гамильтоновых циклов

Пусть объекты (точки) A_t, i = 1, n, заданы значениями m признаков a ik , k = 1, m .

Спрашивается, можно ли считать их однородной группой объектов, и если нет, то, на какие однородные группы они разбиваются.

Будем говорить, что совокупность точек Ai разбивается методом минимальных гамильтоновых циклов на кластеры Q1,Q2,...,QK, если суммарная длина минимальных гамильтоновых циклов у1,у2,...,ук этих кластеров не больше, чем суммарная длина минимальных гамильтоновых циклов кластеров при любом другом разбиении.

Обозначим через С = ( c ij ) матрицу расстояний между точками A i в некоторой выбранной метрике ( евклидовой , квадрата евклидовой и т . д .), будем считать c ii = c, c >>  max( c j ), i * j. Методом от противного доказывается теорема 1.

Теорема 1 . Матрица смежности графа у , состоящего из циклов у 1 , у 2 ,..., у _к , является решением задачи линейного программирования с двоичными (булевыми) переменными:

z = ЕЕ c ij x y ^ ^min, Е x j = 1, Е x j= ^L ij                 i         j

В силу теоремы 1, число кластеров K равно числу компонент связности графа у , каждый кластер Q r состоит из вершин, через которые проходит цикл y r , r = 1, K .

Пример 1. Применяя метод минимальных гамильтоновых циклов, провести классификацию 10 объектов, заданных значениями трех признаков (табл.1).

Таблица 1

Объекты	Признак 1	Признак 2	Признак 3
1.	0,2	2,5	2,3
2.	0,3	2,7	1,8
3.	0,3	2,4	1,6
4.	0,4	2,6	1,6
5.	0,5	2,2	2,4
6.	0,5	2,3	2,2
7.	0,6	2,3	2,5
8.	0,7	2,1	2,1
9.	0,8	2,4	2,1
10.	0,9	2,4	2,5

• 1.    Вводим данные на рабочий лист (рис. 1):

  	А	В	С
  1	0,2	2,5	2,3
  2	0,3	2,7	1.8
  3	0,3	2,4	1.6
  4	0,4	2,6	1.6
  5	0,5	2,2	2.4
  Б	0,5	2,3	2,2
  7	0,6	2,3	2,5
  8	0,7	2,1	2,1
  9	0,8	2,4	2,1
  10	0,9	2,4	2,5

• 2.    Составляя в диапазоне E1:N10 с помощью функции СУММКВРАЗН матрицу расстояний между точками, по главной диагонали ставим 10, получаем (рис. 2):

• 3.    Диапазон E 12 : N 21 оставляем за независимыми двоичными переменными.

• 4.    В ячейку O 12 вводим формулу = СУММ ( E 12 : N 12) и копируем ее в ячейки O 13 : O 21.

• 5.    В ячейку E 22 вводим формулу = СУММ ( E 12 : E 21) и копируем ее в ячейки F 22: N 22.

• 6.    В ячейку     O 22    вводим формулу целевой    функции:

• 7.    Вызываем диалоговое окно «Поиск решения» и задаем сценарий решения (рис. 3).

  
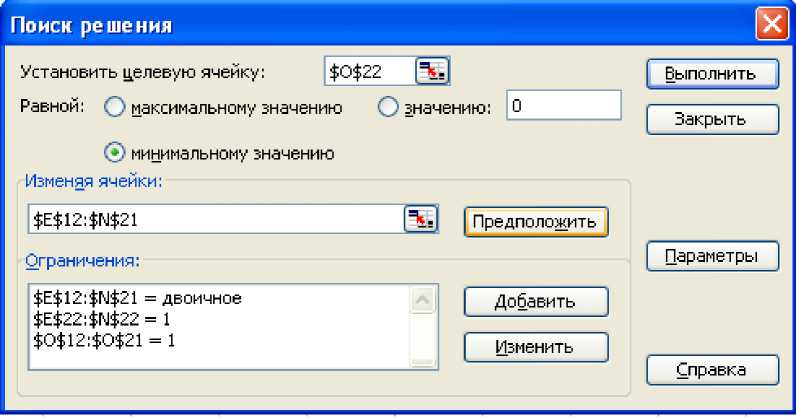8. Команда «Выполнить» в диапазоне E 12 : N 21 возвращает (рис. 4):

0

1

0

2.BE-12

0

0

0

0

0

0

0

0

2.8E-12

1

0

0

0

0

0

0

1

0

0

0

0

0

0

0

2.4E-09

0

0

0

1

0

0

0

0

0

0

0

0

0

0

0

0

0

1

5.9E-10

0

0

0

0

0

0

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

1

0

0

0

0

0

1

5.9E-10

0

0

0

0

0

0

2E-10

0

0

0

1

0

0

0

0

0

0

0

0

0

0

1

0

Е	F	G	H	I	J	К	L	M	N
10	0,3	0,51	0,54	0,19	0,14	0,24	0,45	0,41	0,54
0,3	10	0,13	0,06	0,65	0,36	0,74	0,61	0,43	0,94
0,51	0,13	10	0,05	0,72	0,41	0,91	0,5	0,5	1,17
0,54	0,06	0,05	10	0,81	0,46	0,94	0,59	0,45	1.1
0,19	0,65	0,72	0,81	10	0,05	0,03	0,14	0,22	0,21
0,14	0,36	0,41	0,46	0,05	10	0,1	0,09	0,11	0,26
0,24	0,74	0,91	0,94	0,03	0,1	10	0,21	0,21	0.1
0,45	0,61	0,5	0,59	0,14	0,09	0,21	10	0,1	0,29
0,41	0,43	0,5	0,45	0,22	0,11	0,21	0,1	10	0,17
0,54	0,94	1,17	1,1	0,21	0,26	0,1	0,29	0,17	10

Рисунок 2

= СУММПРОИЗВ(E1:N10;E12:N21).

Рисунок 4

В первой строке значение 1 во втором столбце, т.е. в цикл включается звено (1, 2), во второй строке значение 1 в четвертом столбце, т.е. следующее звено (2, 4). Продолжая цепочку, приходим к циклу γ ₁ : 1 - 2 - 4 - 3 - 1 . Аналогично показывается, что второй цикл γ ₂ : 5 - 7 - 10 - 9 - 8 - 6 - 5 . Следовательно, заданная совокупность объектов разбивается на два кластера {1, 2, 3, 4} и {5, 6, 7, 8, 9, 10}. Графическая иллюстрация, выполненная в пакете STATISTICA, приведена на рисунке 5.

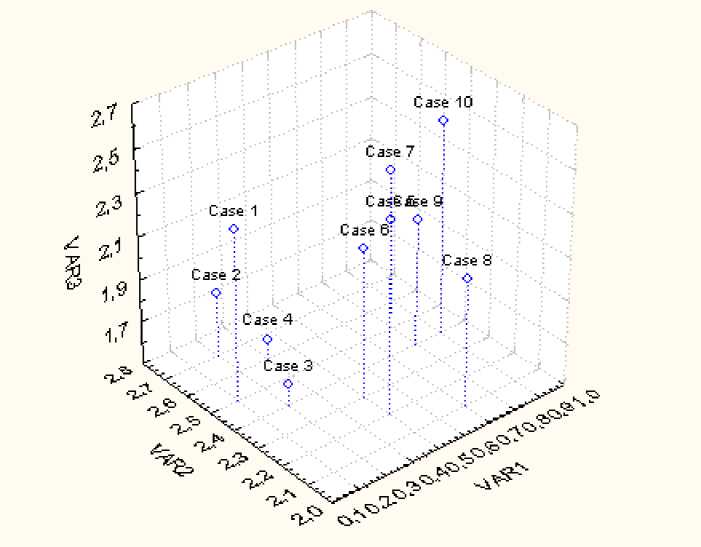
Кластеризация методом минимальных остовных деревьев

Остовным деревом (деревом-остовом) графа G называется дерево T с G, содержащее все вершины графа G. Минимальным остовным деревом называется дерево-остов T с G , имеющее минимальную сумму весовых коэффициентов.

Будем говорить, что совокупность точек A_i разбивается методом минимальных остовных деревьев на кластеры Q 1 , Q 2 ,..., Q K , если суммарная длина минимальных остовных деревьев T ₁ , T ₂ ,..., T_K этих кластеров не больше, чем суммарная длина минимальных остовных деревьев при любом другом разбиении на кластеры.

Составим матрицу D = ( d ij ), d ij = c j , если i <  j , d ij = c , если i >  j , где c >>  max( c j ), i ^ j . Имеет место теорема 2, аналогичная теореме 1.

Теорема 2. При разбиении точек A_i на кластеры методом минимальных остовных деревьев число кластеров равно числу компонент связности графа, матрица смежности которого находится как решение задачи линейного программирования с двоичными переменными:

z = EE d j x j ^ ^min, E x -v + E x ji>^L ijii

Понятно, что вершины каждой компоненты связности образуют кластер.

Пример 2. Применяя метод минимальных остовных деревьев, разбить на кластеры объекты, заданные таблицей 1.

• 1.    Приводим диапазон E1:N10 (рис. 2) к виду (рис. 6):

• 2.    Диапазон E 12 : N 21 оставляем за независимыми двоичными переменными.

• 3.    В ячейку O12 вводим формулу =СУММ(E12:N12)+СУММ(E12:E21), в ячейку О13 – формулу =СУММ(E13:N13)+СУММ(F12:F21) и так далее, до ячейки О21, в которую вводим формулу =СУММ(E21:N21)+СУММ(N12:N21).

• 4.    В ячейку O22 вводим формулу целевой функции: =СУММПРОИЗВ(E1:N10;E12:N21).

• 5.    Вызываем диалоговое окно «Поиск решения» и задаем сценарий решения

• 6.    Команда «Выполнить» в диапазоне E 12 : N 21 возвращает (рис. 8):

EFGHIJKLMN

10	0,3	0,51	0 54	0,19	0,14	0,24	0,45	0,41	0,54
10	10	0 13	0,06	0,65	0,36	0 74	0,61	0,43	0,94
10	10	10	0 05	0 72	0 41	0,91	0 5	0 5	1,17
10	10	10	10	0,81	0,46	0,94	0,59	0.45	1.1
10	10	10	10	10	0.05	0,03	0,14	0,22	0,21
10	10	10	10	10	10	0,1	0,09	0,11	0,26
10	10	10	10	10	10	10	0,21	0,21	0.1
10	10	10	10	10	10	10	10	0 1	0,29
10	10	10	10	10	10	10	10	10	0,17
10	10	10	10	10	10	10	10	10	10

Рисунок 6

(рис. 7).

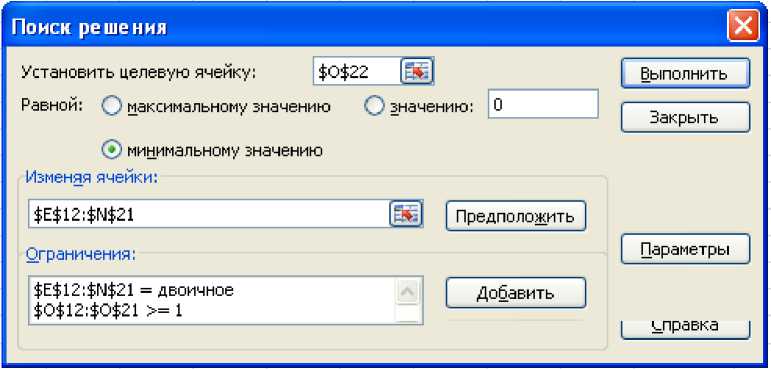
Рисунок 7

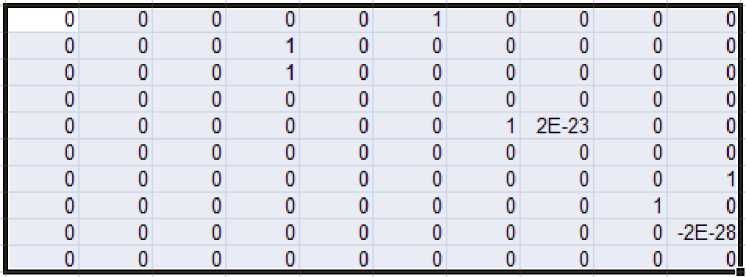
Рисунок 8

Откуда следует, что кластеры {2, 3, 4}, {1, 6}, {5, 7, 10}, {8, 9}.

Теорема 3. Если матрица С = ( c j ) приводится к виду, в котором c 1 k <  c rk , где

• r, k = 2, n, то для метода минимальных остовных деревьев K=1.

Применение макроса Skeleton

Для нахождения минимального остовного дерева разработан макрос Skeleton [5].

Код макроса:

Sub Skeleton()

'Задание массивов с первоначальным разбиением вершин:

ReDim p(1 To 1)

ReDim q(2 To n)

p(1) = 1

For i = 2 To n

q(i) = i

Next

'Нахождение оценки сверху заданных значений:

For k = 1 To n - 1

s = t

For Each x In p

For Each y In q

If y > 0 Then

If Cells(x, y).Value <> Empty And Cells(x, y).Value < s Then s = Cells(x, y).Value a = x: b = y

End If

End If

Next

Next

'Вывод результатов:

Cells(n + 1 + k, 1).Value = a

Cells(n + 1 + k, 2).Value = b

Cells(n + 1 + k, 3).Value = s

'Присоединение к p нового значения:

ReDim Preserve p(1 To 1 + k)

p(k + 1) = b

'Исключение b из q, учитывая y>0:

q(b) = 0

Next

'Вывод минимальной суммы:

Cells(2 * n + 1, 3).Value = Application.WorksheetFunction. _

Sum(Range(Cells(n + 2, 3), Cells(2 * n, 3)))

End Sub

В частности, для данных диапазона E1:N10 рисунка 2 он возвращает (рис. 9):

12	1	6	0,140
13	6	5	0,050
14	5	7	0,030
1^	6	8	0,090
16	7	10	0,100
17	8	9	0,100
18	1	2	0,300
19	2	4	0,060
20	4	3	0,050
21			0,920

Рисунок 9

То есть в минимальное остовное дерево входят дуги (1, 6), (6, 5), (5, 7), (6, 8), (7, 10), (8, 9), (1, 2), (2, 4), (4, 3), в диапазоне С12:С20 – их весовые коэффициенты. Наибольший вес 0,3 имеет дуга (1, 2), удаление ее приводит к двум кластерам (2, 3, 4), (1, 5, 6, 7, 8, 9, 10). После этого дерево, связывающее вершины 1, 5, 6, 7, 8, 9, 10, распадается, если удаляется одна из дуг (5, 7), (6, 8), (5, 6), из которых наибольший вес 0,09 имеет дуга (6, 8). Поэтому разбиение на три кластера получается удалением дуги (6, 8), что дает {2, 3, 4}, {1, 5, 6, 7, 10}, {8, 9}. Следующее разбиение приводит к кластерам, полученным в примере 2.

Заключение

Как следует из изложенного материала, предлагаемые методы минимальных гамильтоновых циклов и минимальных остовных деревьев достаточно эффективны. Единственное, что сдерживает их применение, – ограничения на число независимых переменных, имеющиеся в информационных математических технологиях при решении задач линейного программирования.