Пример формирования уравнений равновесия метода дополнительных конечных элементов для расчета железобетонных балок-стенок по предельным состояниям

Введение. Нормы проектирования железобетонных конструкций основаны на их расчете по методу предельного равновесия [1]. Реализация такого расчета невозможна без учета всех физически нелинейных свойств, проявляемых этой конструкцией к моменту достижения ею предельного состояния (состояния предельного равновесия). Разработанный метод дополнительных конечных элементов (МДКЭ) [2] предназначен для решения этой задачи.

Общие сведения о МДКЭ. Метод дополнительных конечных элементов представляет собой вариант метода конечных элементов (МКЭ), предназначенный для нелинейного расчета плоских железобетонных конструкций по предельным состояниям. К традиционной последовательности решения задачи МКЭ он добавляет операции метода предельного равновесия и метода упругих решений (дополнительных нагрузок) [3].

Решение основной проблемы в МДКЭ. Расчет по предельным состояниям является одним из видов нелинейного расчета. Анализ проблем, связанных с его реализацией [4], позволил выделить из них ту, без решения которой такую реализацию осуществить невозможно. Эта проблема связана с формированием уравнений равновесия каждого из узлов расчетной схемы конструкции, поскольку основной математической операцией МКЭ является решение системы из этих линейных алгебраических уравнений. Трудность заключается в том, что при нелинейном расчете эти уравнения должны меняться в зависимости от степени проявления тех или иных нелинейных свойств. Это требует использования различных теоретических моделей поведения железобетонных конструкций, например [5, 6].

Уравнения равновесия формируются на основе узловых реакций каждого из КЭ расчетной схемы. Требуется способ постепенного изменения этих уравнений в зависимости от стадии нелинейного расчета. Этот способ должен отражать влияние каждого из нелинейных свойств, которое проявляется в данный момент работы конструкции. МДКЭ предлагает для решения этой проблемы использовать дополнительные конечные элементы (ДКЭ) [7, 8].

Далее этот вопрос рассмотрен подробнее на простом примере формирования уравнений равновесия для нелинейного расчета изгибаемой бетонной консоли с помощью МДКЭ. Ее исходная расчетная схема состоит из восьми КЭ и имеет девять узлов (рис. 1).

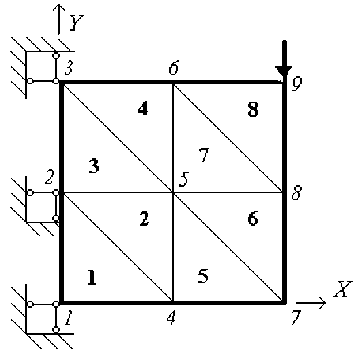
Рис. 1. Исходная расчетная схема изгибаемой бетонной консоли из треугольных КЭ балки-стенки с линейными свойствами

" R 86 " R w 6 R 88 R w 8 R u ⁸9

_ R w9 _

88 88 88

u 6 u 6 ^Ku 6 w 6 ^Ku 6 u 8 ^Ku 6 w 8 ^Ku 6 u 9 ^Ku 6 w 9

888888 w 6 u 6 ^Kw 6 w 6 ^Kw 6 u 8 ^Kw 6 w 8 ^Kw 6 u 9 ^Kw 6 w 9

u 8 u 6 ^Ku 8 w 6 ^Ku 8 u 8 ^Ku 8 w 8 ^Ku 8 u 9 ^Ku 8 w 9

888888 w 8 u 6 ^Kw 8 w 6 ^Kw 8 u 8 ^Kw 8 w 8 ^Kw 8 u 9 ^Kw 8 w 9

u 9 u 6 ^Ku 9 w 6 ^Ku 9 u 8 ^Ku 9 w 8 ^Ku 9 u 9 ^Ku 9 w 9

888888 w 9 u 6 ^Kw 9 w 6 ^Kw 9 u 8 ^Kw 9 w 8 ^Kw 9 u 9 ^Kw 9 w 9

u 6 w 6

u 8

w 8 u 9

w 9

Далее приведены уравнения равновесия для узлов № 4, 6 и 9, так как именно в этих узлах сходятся КЭ с характерными для данной задачи физически нелинейными свойствами. Каждый из узлов имеет два перемещения: вертикальное u и горизонтальное w . Для каждого из узлов расчетной схемы формируются два уравнения равновесия.

На начальном этапе МДКЭ использует уравнения равновесия МКЭ, примеры формирования которых для подобных линейных задач представлены в [9, 10].

Уравнения равновесия узлов линейной задачи МКЭ. Узел № 9 принадлежит только одному КЭ № 8, поэтому для него уравнения равновесия записываются более простым способом, чем для двух других узлов. В этом узле приложена внешняя вертикальная сила P , поэтому эти уравнения принимают вид:

где u 6 , u 8 , u 9 и w 6 , w 8 , w 9 – вертикальные и горизонтальные перемещения узлов № 6, 8 и 9; а K_u ⁸ _{9 u 6} ,

8 8888  8

^Ku 9 w 6 , ^Ku 9 u 8 , ^Ku 9 w 8 , ^Ku 9 u 9 , ^Ku 9 w 9 и ^Kw 9 w 6 ,

K w ⁸9 w 6 , K w ⁸9 u 8 , K w ⁸9 w 8 , K w ⁸9 u 9 , K w ⁸9 w 9 – элементы матрицы жесткости КЭ № 8 с линейными свойствами, определяющие величины вертикальных и горизонтальных реакций в узле № 9 от единичных смещений u 6 , w 6 , u 8 , w 8 , u 9 , w 9 ; R_u ⁸ ₆ , R_u ⁸ ₈ , R_u ⁸ ₉ и

R_w ⁸ ₆ , R_w ⁸ ₈ , R_w ⁸ ₉ – вертикальные и горизонтальные

реакции узлов № 6, 8 и 9.

Поскольку речь идет об уравнениях равновесия

узла № 9, то рассматриваются реакции только этого

R u 9 = p ;

R w 9 = 0,

узла, которые определяются из выражения (4): 88    8    8

^Ru 9 = K u 9 u 6 ^u 6 ⁺ K u 9 w 6 ^w 6 ⁺ K u 9 u 8 ^u 8 ⁺

• ■ K u 9 w 8 w 8 + K 89 u 9 u 9 + K 9 w 9 W 9 ^

• ^Rw9 = K w 9 u 6 ^u 6 ⁺ K w 9 w 6 ^w6 ⁺ K w 9 u 8 ^u 8 ⁺

8              8           J^8

| + K w 9 w 8 ^w 8 ⁺ K w 9 u 9 ^u 9 ⁺ K w 9 w 9 ^w 9 -

Уравнения равновесия (1) с учетом (2) при-

где R u 9 и R w 9 – вертикальная и горизонтальная реакции в узле № 9 КЭ с линейными свойствами. Эти реакции определяются свойствами только одного КЭ № 8:

R u 9 = R 89

нимают вид:

K u 9 u 6 ^u 6 ⁺ K u 9 w 6 ^w 6 ⁺ K u 9 u 8 ^u 8 ⁺ K u 9 w 8 ^w 8 ⁺

/ K «9 u 9 u 9 + K 89 w 9 w 9 = P ;

K w9 u 6 u 6 + K w9 w 6 w 6 + K w9 u 8 u 8 + K w9 w 8 w 8 +

и

.^{+ K}w 9 u 9 ^u 9 ^{+ K}w 9 w 9 ^w 9 = °.

Rw 9 = Rw9, где Ru89 и Rw89 – вертикальная и горизонтальная реакции в узле № 9 КЭ № 8.

Для данного КЭ, как и для любого другого, справедлива следующая зависимость между узловыми реакциями R и перемещениями узлов V :

В этом виде они и входят в основную разрешающую систему уравнений для расчета этой изгибаемой консоли МКЭ.

Для узла № 6 уравнения равновесия выглядят так:

R = KV ,

R u 6 = °;

R w 6 = °,

где K – матрица жесткости КЭ.

В матричном виде это соотношение выглядит так

где R u 6 и R w 6 – вертикальная и горизонтальная реакции в узле № 6, которые определяются тремя сходящимися в этом узле КЭ с линейными свойствами № 4, 7 и 8:

R u 6 = R 6 + R 76 + R 86 ; R w 6 = R W + R 76 + R W   (8)

где R_u ⁴ ₆ , R_u ⁷ ₆ , R_u ⁸ ₆ и R_w ⁴ ₆ , R_w ⁷ ₆ , R_w ⁸ ₆ – вертикальные и

,

горизонтальные реакции в узле № 6 КЭ № 4 ( i = 6 j = 3 и k = 5), № 7 ( i = 6, j = 5 и k = 8) и № 8 ( i = 6

,

j = 8 и k = 9). Эти величины определяются по формулам, аналогичным (5):

<

<

<

R 46 = ^Ки46 u 3 ^u 3 ⁺ K 6 w 3 ^w3 ^{+ К}и 6 u 5 ^u 5 ⁺

• ⁺ Ku6 w 5 ^w5 ⁺ Ku6 и 6 ^u 6 ⁺ Ku6 w 6 ^w 6 ;

• ^Rw 6 = Kw6 u 3 ^u 3 ⁺ K w6 w 3 ^w3 ⁺ K w6 u 5 ^u 5 ⁺

• ⁺ K 46 w 5 ^w5 ⁺ K 46 u 6 ^u 6 ⁺ K 46 w 6 ^w 6^;

R u ⁷6 = K 76 u 5 u 5 + K u ⁷6 w 5 W + K 76 u 6 « 6 +

• ^{+ K}u 6 w 6 ^w6 ⁺ Ku6и 8 ^u 8 ⁺ Ku6w 8 ^w 8 ;            (9)

• ^Rw6 = K w6 u 5 ^u 5 ⁺ Kw6 w 5 ^w5 ⁺ Kw6 u 6 ^u 6 ⁺

• ⁺ K w6 w 6 ^w6 ^{+ K}w 6 u 8 ^u 8 ^{+ K}w 6 w 8 ^w 8^;

R u 6 = ^Ku 6 u 6 ^u 6 ^{+ K}u 6 w 6 ^W6 ^{+ K}u 6 u 8 ^u 8 ⁺

• ⁺ Ku6 w 8 ^w 8 ^{+ К} и6 u 9 ^u 9 ⁺ Ku6 w 9 ^w 9 ; 88    8    8

R w 6 = K w 6 u 6 ^u 6 ⁺ K w 6 w 6 ^w6 ⁺ K w 6 u 8 ^u 8 ⁺

+ K w 6 w 8 w 8 + K w 6 u 9 u 9 + K^& w6 w 9 w 9 .

Используя выражения (8), уравнения равновесия (7) записываются так:

1 1 + RW X.

Если в эту формулу подставить значения узловых реакций из (9), то можно получить полную форму, в которой эти уравнений равновесия для узла № 6 входят в основную систему уравнений МКЭ.

Уравнения равновесия для узла № 4 имеют вид:

R 4 = 0;

R w 4 = 0,

где R_{u 4} и R_{w 4} – вертикальная и горизонтальная реакции в узле № 4, которые определяются тремя сходящимися в этом узле конечными элементами с линейными свойствами: КЭ № 1, КЭ № 2 и КЭ № 5. Поэтому

R u 4 = R 14 + R 24 + Ru 4

и

Rw 4 = RW 4 + R 4 + R ■ где Ru14,Ru24,Ru54и R1w4,Rw24,Rw54 – вертикальные и горизонтальные реакции в узле № 4 в КЭ № 1 (i = 4, j = 2 и k = 1), № 2 (i = 4, j = 5 и k = 2) и № 5 (i = 4, j = 7 и k = 5).

В этом случае выражение (11) принимают вид:

I : R W S.

Величины вертикальных Ru14,Ru24,Ru54 и гори зонтальных R1w4,Rw24,Rw54 узловых реакций опре- деляются по формулам, аналогичным (5) при соответствующих значениях номеров узлов № 1, 2 и 5.

Если полученные после этого значения подставить в выражение (13), то можно получить полную форму уравнений равновесия для узла № 4 для основной системы уравнений.

В результате уравнения равновесия для узлов № 9, 6 и 4 имеют вид (1), (10) и (13) соответст- венно.

Уравнения равновесия узлов нелинейной задачи МДКЭ. Особенностью нелинейного расчета железобетонных конструкций по предельным состояниям является то, что физически нелинейные свойства постепенно проявляются при работе конструкции по мере достижения ею предельного состояния. Это означает, что исходная расчетная схема должна превратиться в идеальную модель разрушения, т. е. расчетную схему конструкции в предельном состоянии.

Этот процесс должен быть отражен постепенным изменением линейных уравнений равновесия. Для этого МДКЭ [11] предлагает подключить операции метода упругих решений (дополнительных нагрузок) [12].

Так, например, при появлении первого нелинейного свойства, которым обычно является пластичность бетона, систему уравнений равновесия (1) узла № 9 можно записать так:

' ( K u ⁸9 u 6 + A K u^u 6 ) u 6 + ( K u ⁸9 w 6 + A K u X 6 ) w 6 +

+ ( K u ⁸9 u 8 +A K 9¹ u 8 ) u 8 + ( K 89 8 + AK^ )w . +

< + ( K u ⁸ ₉ u 9 +A K u ⁸91 u 9 ) u 9 + ( K u ⁸9 „ 9 +A K u ⁸91 _W 9 ) w 9 = P; ₍₁₄₎ ' ( K ^ 9 u 6 + A K ^ -9 u 6 ) u 6 + ( k w w 6 +AKW w 6 ) w 6 +

+ ( K W 9 u 8 +A K W9 u 8 ) u 8 + ( K W 9 w 8 + A K^ „ 8 ) „ 8 +

.= ( K W 9 u 9 +A K W1 u 9)u 9 + ( K W _w 9 +A K W 9 „ 9 ) W 9 = 0.

Здесь A K u ⁸91 u 6 , A K u ⁸91 w 6 , A K 891 u 8 , A K u ⁸91 w 8 , A K 891 u 9 ,

8,1               8,1               8,1                8,1               8,1

^{A K}u 9 w 9 , ^{A K}w 9 u 6 , ^{A K} w 9 w 6 , ^{A K}w 9 u 8 , ^{A K}w 9 w 8 , A kW 9 _{u 9} , A K W 9 _{w 9} - элементы матрицы жесткости ДКЭ № 8. Этот ДКЭ превращает КЭ № 8 с линейными свойствами в этот же КЭ № 8, но с наличием первого нелинейного свойства (пластичностью бетона).

Между матрицей жесткости K ⁸ КЭ № 8 с линейными свойствами, матрицей жесткости K ^8,1 КЭ

№ 8 с первым нелинейным свойством и матрицей жесткости A K ^8,1 ДКЭ № 8, предназначенного для учета этого нелинейного свойства, существует следующая взаимосвязь:

K ^8,1 = K ⁸ +A K ^8,1 . (15)

Отдельные элементы этих матриц связаны между собой согласно этому соотношению. Например:

K uL 6 = K 89 W 6 +AK^ w 6 . (16)

Раскрывая скобки и перенося все слагаемые, связанные с ДКЭ, эту систему уравнений (14)

можно превратить в другую:

Ku9 и 6 ^u 6 ^{+ K}u9 w 6 ^w 6 ^{+ K}u9 u 8 ^u 8 ^{+ K}u 9 w 8 ^w 8 ⁺

^{+ K}u9u 9 u 9 ⁺ K u 9 w 9 ^w 9 = P ^-A K ₁Mu 6 ^u 6 ^-A K u 9 w 6 ^w 6 ^-

_< -AK^ 8 u -A K^ w -AK^ 9 u k -AK^ W 9 ;

^Kv9 u 6 ^u 6 ^{+ K}w 9 w 6 ^w 6 ^{+ K}w 9 u 8 ^u 8 ^{+ K}w 9 w 8 ^w 8 ⁺

^{+ K}w9 u 9 u 9 ^{+ K}w9 w 9 ^w 9 ^{= -A} K w 9 u 6 ^u 6 ^-A K w 9 w 6 ^w6 ^- "K u 8 u 8 A K⁸ w 8 W 8 A K . u 9 u 9 - K w 9 ” 9 -

В результате при наличии первого нелинейного свойства уравнения равновесия узла № 9 исходную форму (1) меняют на (21). При дальнейшем увеличении силы Р эта форма остается неизменной, так как в КЭ № 8 вплоть до наступления предельного состояния этой консоли наблюдается только одно нелинейное свойство, а именно, пластичность бетона.

Уравнения равновесия для узла № 6 в зависи-

мости от величины действующей вертикальной

нагрузки Р и могут принимать три разных вида. До

образования трещины во всех трех КЭ № 4, 7 и 8

Вертикальные A R_u 9 и горизонтальные A R_w 9

проявляются только пластические свойства бетона

узловые реакции ДКЭ № 8 определяются по фор-

мулам:

'A R = A K X 6 u 6 +A K ⁸9 w 6 W 6 -AK' 8 u 8 +

, +A K u ⁸9 w 8 W 8 -A K ' ¹ 9 u 9 +A K ⁸9 w 9 W^;

' A R W 9 = A K w u 6 u 6 +A K W 9 w 6 W 6 ■ A K. u 8 u 8 +

■A K . w 8 W j +A K W 9 u 9 u 9 +A K w 9 w 9 w 9 .

и поэтому уравнения (10) и (21) принимают вид:

/ R u ⁴6 + R Js + R u ⁸6 = -A R u ⁴61 - A R⁷¹ -AR 861 ; (2 _ R w6 + R w 6 + R w 6 = -AR w6 - A R w 6 - A R w 6 ,

где A R u ⁴61 , A R ^61 , A R ⁸6 и A R w 6 , A R w 61 , A R w 6

–

Подставив это выражение (18) в соотношение

(17) можно получить для узла № 9 такие уравне-

ния равновесия:

^Ku9 u 6 ^u 6 ⁺ K ⁸9 w 6 ^w 6 ^{+ K}u9 u 8 ^u 8 ^{+ K} 89 w 8 ^w 8 ⁺

^{+ K}u9 u 9 ^u 9 ^{+ K}u 9 w 9 ^w 9 = P ^{- A R} 891 ;

K w9 u 6 ^u 6 ⁺ K w9 w 6 ^w 6 ⁺ K w9 u 8 ^u 8 ⁺ K w 9 w 8 ^w 8 ⁺

, ⁺ K w 9 u 9 ^u 9 ⁺ K w 9 w 9 ^w 9 = ^{-A R} ^ 9 "

вертикальные и горизонтальные реакции в узле № 6 ДКЭ № 4, 7 и 8 для учета пластических свойств соответствующих КЭ.

При образовании трещины в КЭ № 4 происходит частичная разгрузка и перераспределение усилий, т. е. появляется второе нелинейное свойство. При этом уравнения равновесия (22) меняются:

' R 46 + R u ⁷6 + R 86 =

rw6+rw6+rw6 =

8,1 u 6 ;

Учитывая что узел № 9 принадлежит только одному КЭ № 8 и следовательно только одному ДКЭ № 8 можно сделать следующее заключение:

A R u 9 =A R u ⁸91

4,1 w 6

4,2 w 6

7,1 w 6

-A R

8,1 w 6 ,

42      42

где A R_{u 6} ^, и A R_w ^, ₆ - вертикальная и горизонтальная

и

A R w 9 =A R w 9 ,

где A R u 9 , A R_w 9 - величины изменения вертикаль-

ной R u 9 и горизонтальной R w 9 реакций узла № 9 за счет проявления пластических свойств бетона, т. е.

реакции в узле № 6 ДКЭ № 4 для учета частичной разгрузки в КЭ № 4.

После образования трещины в КЭ № 4, т. е. при наличии третьего нелинейного свойства, вплоть до наступления предельного состояния в КЭ № 1 уравнения равновесия узла № 6 таковы:

' R 46 + R u ⁷6 + R 86 =

первого нелинейного свойства.

В результате уравнения (1) для узла № 9 принимают следующую форму:

4,1       4,2

^Lu 6    ^{A R} u 6

-

A R ^4,3 u 6

-

7,1 u 6

8,1 u 6 ;

rw6+rw6+rw6 =

.R 89 = P -A R 89¹ ; . r w 9 =-a r w 9 .

Сравнивая соотношения (1) и (21), можно сделать вывод о том, что величины ( -A R 89¹ ) и

( -A R w 9 ) представляют собой часть вертикальной

и горизонтальной дополнительной нагрузки, которую нужно добавить к внешней силе Р , действующей на изгибаемую консоль с линейными свойствами, чтобы получить перемещения узлов, соответствующие ее перемещениям под действием одной только внешней силы Р при наличии пластических свойств.

4,1 w 6

4,2 w 6

-

A R ⁴k³

w 6

-

7,1 w 6

8,1 w 6 ,

где A R_u ⁴ ₆ ^,3 и A R_w ^4, ₆ ³ - вертикальная и горизонтальная

реакции в узле № 6 ДКЭ № 4 для учета наличия трещины в КЭ № 4. Таким образом, уравнения равновесия для этого узла (10) сначала принимают вид (22), затем (23) и наконец (24).

Для узла № 4 уравнения равновесия записываются двумя способами. Вначале при наличии пластических свойств во всех трех сходящихся в этом узле КЭ они имеют вид, аналогичный (22):

R 14 + R u ²4 + R 54 = -A R u 4 - A R u ²41 - A R 54 ;

R w 4 + R w 4 + R ^4 = -A R w 4 -A R w 4 - A R w 4 ,

где A R 1,1 , AR. , A R 51 и A R ^, A R , A R W 1 - вер-

тикальные и горизонтальные реакции в узле № 4 ДКЭ № 1, 2 и 5 для учета пластических свойств соответствующих КЭ.

Во втором случае при возникновении предельного состояния на сжатие в КЭ № 1, посколь-

ку в нем не может образоваться трещина из-за рас-

тягивающих напряжений, они записываются так:

R 14 + R 24 + R 54 =

^^^^^^e

a r 14

^^^^^^e

1,4 u 4

2,1 u 4

5,1 u 4 ;

R W 4 + R ^ 4 + R ^ 4 =

-A R W4 -A R W4 -A R W 4 -A R W 4 ,

где A R U4 и A R W4 - вертикальная и горизонтальная реакция в узле № 4 ДКЭ № 1 для полного исключения из работы КЭ № 1.

Уравнения равновесия этого узла № 4 также изменяют свой первоначальный вид (13) на (25), а потом в предельном состоянии на (26).

Таким образом, МДКЭ дает способ изменения уравнений равновесия узлов № 4, 6 и 9 в соответствии с этапами нелинейной работы от начала за-гружения до наступления ее предельного состояния. В результате получена идеальная модель разрушения данной консоли, представленная на рис. 2.

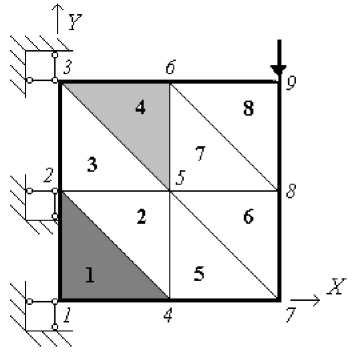
Рис. 2. Идеальная модель разрушения изгибаемой бетонной консоли в МДКЭ: КЭ № 1 в предельном состоянии, КЭ № 4 с трещиной

Выводы. Предлагаемый МДКЭ способ формирования уравнений равновесия позволяет:

• 1)    рационально строить итерационный процесс при решении системы уравнений, используя все преимущества метода упругих решений (дополнительных нагрузок);

• 2)    реализовать нелинейной расчет железобетонных конструкций по предельным состояниям, как это требуют нормы проектирования;

3) вводить различные теоретические модели поведения железобетонных конструкций по мере достижения предельного состояния.

Его эффективность была подтверждена расчетом ряда железобетонных конструкций, работающих в условиях плоского напряженного состояния, а также расчетом пространственной оболочки покрытия.