Примеси кремния в ОЦК-железе: ab-initio моделирование свойств и энергетических параметров

Сплавы на основе железа, несмотря на развитие производства других металлов, пластмасс, керамики, композитов, остаются основными конструкционными материалами. Исключительным достоинством черных металлов является, прежде всего, их дешевизна, а также универсальность – при помощи небольших добавок можно резко изменить свойства их сплавов. Бинарные сплавы железа Fe–C [1–3] и Fe–Si [4–6] методами компьютерного моделирования уже изучены довольно подробно. На данный момент представляют интерес расчеты тройных сплавов, например Fe–Si–C, используемые как конструкционные и как магнитомягкие материалы. Методами компьютерного моделирования для системы Fe–C [1–2] все оптимальные параметры уже установлены, необходимо провести оптимизацию параметров моделирования в системе Fe–Si.

Методика

В данной работе расчеты проводись пер-вопринципным полнопотенциальным методом LAPW [7], с учетом обобщенного градиентного приближения PBE-GGA в программном пакете WIEN2k [8]. ОЦК-железо моделирова- лось в суперячейке, состоящей из 54 атомов железа. Для расчетов использовался вычислительный комплекс ЮУрГУ-Торнадо [9]. Основные параметры моделирования были установлены в работе [1]: RmtKmax = 10, радиусы MT-сфер – Rmt(Fe) = 2,00 a.е., Ecut = –7 Рб, Gmax = 20 Рб0,5. Для интегрирования в обратном пространстве и вычисления электронной плотности использовалась схема Монхорста – Пака [10] с сеткой 4x4x4 к-точек в зоне Бриллюэна. Данные параметры моделирования обеспечили точность расчета энергии системы в 0,01 эВ.

Оптимизация параметров моделирования

Анализ работ других авторов, где моделировались эффекты добавления кремния в программном пакете WIEN2k [4,11–14], показал, что наблюдается определенный разброс значения R mt (Si), поэтому было выбрано несколько первоначальных радиусов R mt (Si) = 1,8; 1,9; 2,0; 2,1 a.е. Оптимизация параметра решетки с данными параметрами МТ-сфер Si позволила получить оптимальный параметр решетки (рис. 1) a = 2,835 Å, что совпадает с параметром решетки чистого ОЦК-железа. При изменении R mt (Si) происходило

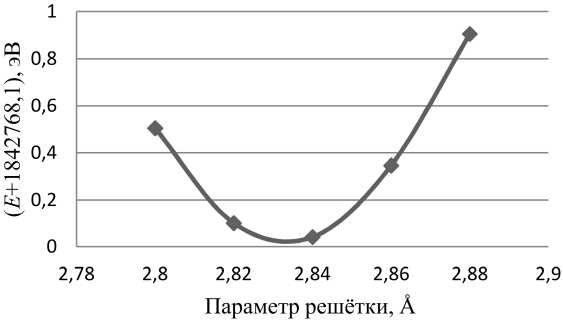
Рис. 1. Зависимость полной энергии системы от параметра решетки

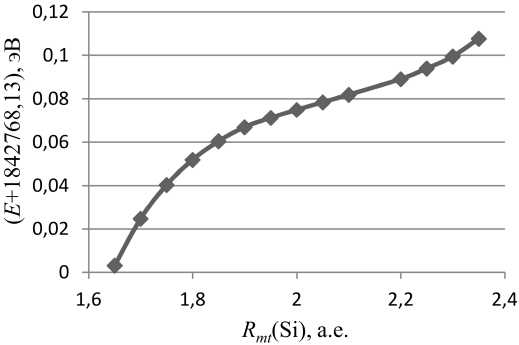
Рис. 2. Зависимость полной энергии системы от R_mt (Si)

незначительное увеличение параметра решетки в третьем знаке после запятой, что при округлении не повлияло на результат.

После получения оптимального параметра решетки была проведена оптимизация R mt (Si). Как видно из графика на рис. 2, в данном случае также не наблюдается минимум полной энергии, а лишь перегиб в районе 2,0 а.е. Так как по данным многих работ известно, что радиусы железа и кремния примерно равны, решено было выбрать R mt (Si) = = R mt (Fe) = 2,00 a.е.

Моделирование растворения кремния

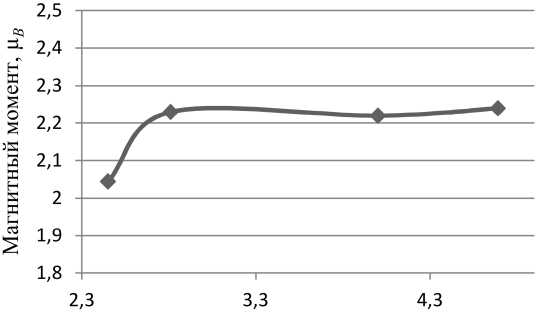
При растворении кремний изменяет магнитные моменты атомов железа в своем окружении (рис. 3). Магнитный момент атомов железа в первом окружении с 2,23 µB, уменьшается до 2,045 µB. Растворение кремния не приводит к изменению параметра решетки системы и возникновению тетрагональности (рис. 4). Это неудивительно, поскольку кремний является примесью замещения, а не вне- дрения, и к тому же атомный радиус кремния близок к атомному радиусу железа.

Магнитный момент кремния составил μ Si = –0,09 µ B (знак минус означает, что магнитный момент атома кремния развернут противоположно магнитному моменту атомов железа). Сравнение рассчитанных нами полных и парциальных электронных плотностей на атомах железа первой и второй координационной сферы вблизи растворенного атома кремния с данными для чистого железа приведены в табл. 1 и на рис. 5.

Из анализа рис. 5 и табл. 1 видно, что серьезного изменения электронной плотности не произошло, потому что электроотрицательности кремния и железа близки. Однако наблюдается небольшая гибридизация p -орбиталей кремния с d -орбиталями t 2 g -типа атомов железа в первой координационной сфере.

Энтальпия растворения кремния в ОЦК-железе оценивалась по формуле

Δ H (Si) = E (Fe53Si) – (53/54)· E (Fe54) –

– (1/8)· E (Si8),

Физическая химия и физика металлургических систем

где E (Fe54) энергия отрелаксированной су-перячейки, состоящей из 54 атомов железа; E (Fe53Si) – энергия отрелаксированной су-перячейки, состоящей из 53 атомов железа и одного атома кремния; E (Si8) – энергия супер-ячейки из 8 атомов кремния. Кремний моделировался в решетке алмаза с параметром решетки, взятым из работы Окада [15] a = 5,43 Å.

Энтальпия растворения составила –1,19 эВ, что находится в хорошем согласии со значением –1,12 эВ, полученным в работе Винсента [5] и –1,2 эВ, полученным в работе Петрика [6].

Энергия взаимодействия между атомами кремния оценивалась по формуле

Δ E = E (Fe52Si2) – 2· E (Fe53Si) + E (Fe54),

Расстояние, А

Рис. 3. Зависимость магнитного момента на атоме железа от расстояния до атома кремния

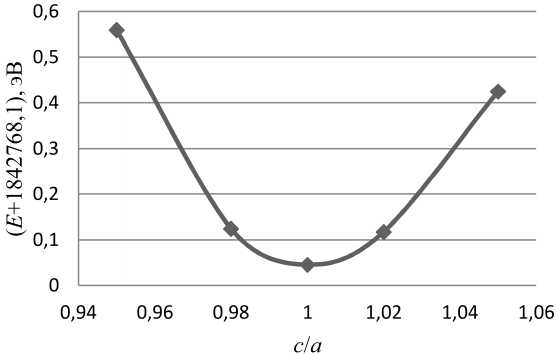
Рис. 4. Зависимость полной энергии системы от тетрагональности c/a

Таблица 1

Значения валентной (для уровней выше 2 S ) электронной плотности для s , p , d , d-e_g и d-t _{2 g} подуровней в атомах железа, находящихся в первой и второй координационных сферах от атома кремния

	Первое окружение				Второе окружение
Спин электронов	Вверх		Вниз		Вверх		Вниз
Суперячейка	Fe54	Fe53Si	Fe54	Fe53Si	Fe54	Fe53Si	Fe54	Fe53Si
s	1,12	1,11	1,11	1,12	1,12	1,12	1,11	1,12
p	3,08	3,08	3,09	3,09	3,08	3,08	3,09	3,09
d	3,97	3,89	1,72	1,83	3,97	3,97	1,72	1,72
d-e g	1,68	1,68	0,46	0,5	1,68	1,7	0,46	0,43
d-t 2 g	2,29	2,21	1,24	1,33	2,29	2,27	1,24	1,29

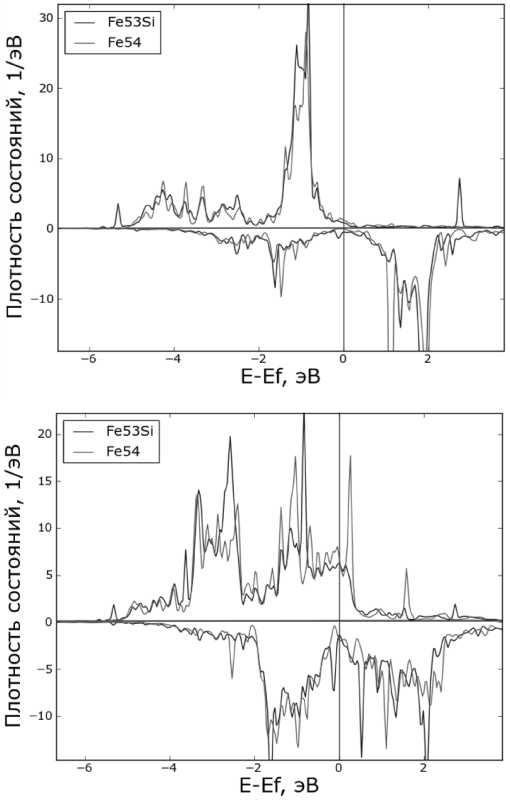
Рис. 5. Графики электронной плотности d-состояний атомов железа в первом окружении. Сверху электронная плотность d-eg состояний, снизу d-t2g

где E (Fe52Si2) – энергия отрелаксированной суперячейки, состоящей из 52 атомов железа и двух атомов кремния (рис. 6). Энергии взаим одействия между атомами кремния предста влены в табл. 2.

Как видно из табл. 2, атомы кремния сильно отталкиваются в первых двух координационных сферах. После третьей координационной сферы отталкивание становится близким к нулю. Наши данные близки к дан-

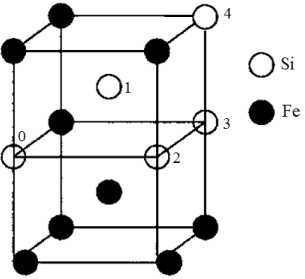
Рис. 6. Черные круги – атомы железа, белые круги – атомы кремния. Цифрами обозначены координационные сферы атома кремния. Отсчет идет от атома номер ноль

Таблица 2

Энергии взаимодействия между атомами кремния, растворенными в ОЦК-железе, эВ

Номер координационной сферы	Данная работа	Винсент [5]
1	0,39	0,29
2	0,2	0,2
3	0,01	–
4	0,03	—

Физическая химия и физика металлургических систем

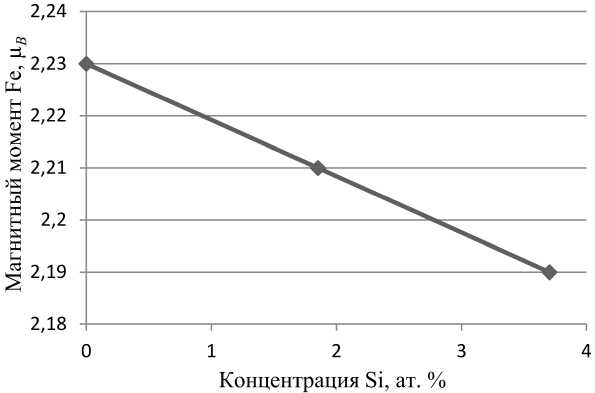
Рис. 7. Зависимость среднего магнитного момента на атоме железа от концентрации кремния в ат. %

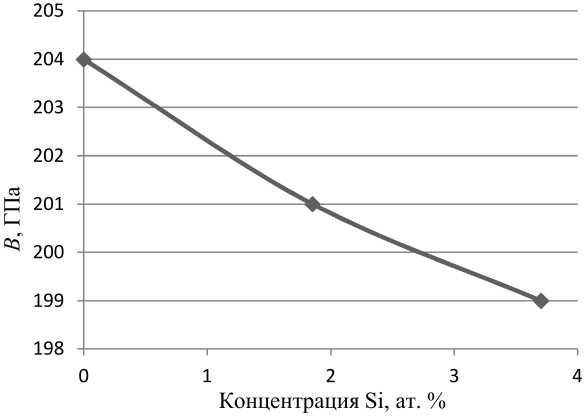
Рис. 8. Зависимость объемного модуля B от концентрации кремния в ат. %

ным работы [5]; разница наблюдается для первой координационной сферы. Отличие энергий составляет 0,1 эВ. Причина этого – использование в работе [5] псевдопотенци-альных методов, которые являются менее точными, чем полнопотенциальные. Благодаря отталкиванию расстояние между атомами кремния, когда они находятся в первой координационной сфере, увеличилось на 0,21 Å, во второй координационной сфере оно увеличилось на 0,14 Å. В последующих координационных сферах не было изменения геометрической структуры.

При растворении кремния магнитный момент на атом железа в суперячейке уменьшается (рис. 7). Растворение 1,85 ат. % кремния (один атом кремния на суперячейку из

54 атомов железа) приводит к уменьшению среднего магнитного момента на атом железа на 0,02 μ B .

Одновременно с понижением средних магнитных моментов атомов железа было обнаружено уменьшение объемного модуля сплава. Полученные нами результаты приведены на рис. 8. При легировании кремнием в железе ослабевают силы межатомного отталкивания, что и приводит к снижению объемного модуля.

Заключение

Определены оптимальные значения основных параметров моделирования примесей кремния в ОЦК-железе, позволяющие рассчитывать энергетические характеристики систе- мы с точностью не менее 0,01 эВ в программном пакете WIEN2k. Показано, что:

• 1)    оптимальный радиус МТ-сферы кремния равен R mt (Si) = 2,00 a.е.;

• 2)    при растворении в пределах изученных концентраций кремний не изменяет параметр решетки и не влияет на решетку железа. Магнитный момент атомов железа в первом окружении с 2,23 µ B , уменьшается до 2,045 µ B . Растворение 1,85 ат. % кремния приводит к уменьшению среднего магнитного момента на атом железа на 0,02 μ B и объемного модуля сжатия. Происходит небольшая гибридизация p -орбиталей кремния с d -орбиталями t 2 g -типа атомов железа в первой координационной сфере;

• 3)    с использованием найденных значений параметров моделирования проведено вычисление энергии растворения атома кремния в ферромагнитной фазе ОЦК-железа, которая составила –1,19 эВ, что находится в хорошем согласии с результатами эксперимента и других первопринципных расчетов;

• 4)    атомы кремния испытывают сильное отталкивание в первых двух координационных сферах, которое является спадающим. После третьей координационной сферы отталкивание атомов становится близким к нулю.

Исследование выполнено за счет гранта Российского научного фонда № 16-19-10252.