Принцип максимума для решения уравнения эллиптического типа с неограниченными коэффициентами

Если максимум и минимум значений некоторой величины достигаются на границе рассматриваемой области, то говорят, что такая величина подчиняется принципу максимума. Решения простейших уравнений в частных производных эллиптического типа, как правило, подчиняются принципу максимума [1–4]. Принцип максимума той или иной величины используется при качественном анализе процесса и для априорных оценок. Поэтому в прикладной математике периодически будут появляться задачи поиска параметров процесса, подчиняющихся принципу максимума, и доказательства соответствующих утверждений. Но в некоторых случаях не удается применить ни общеизвестные [1–4] теоремы, ни приёмы их доказательства. В качестве примера можно привести задачу об установившемся осесимметричном течении вязкой несжимаемой жидкости. Для исследования осесимметричных течений обычно вводят цилиндрическую систему координат г, у, г с началом в точке О так, чтобы течение оказалось осесимметричным относительно оси Ог. В таких координатах уравнение Навье — Стокса для окружной компоненты скорости жидкости V ф имеет вид [5, с. 563]:

д        д ..   VфVr     / д2      1 д      Уф   д2\

• У% тт" ^ ⁺ ^ тт" У ф +— ^v I     У ф +— тг" У ф 7 + т;—9 ^Vt P ) ,

дг        дг г       \ дг2      г дг      г2   дг2/ где VT и Уф — радиальная и осевая компоненты скорости соответственно, v > 0 — кинематический коэффициент вязкости. Если выразить окружную компоненту скорости Уф через окружную циркуляцию скорости 7 — 2тгУф, то последнее уравнение принимает вид

Поскольку ограниченность V _T и V _z является естественным свойством ламинарного течения, величина ( V _r + 7 не ограничена в окрестности точек, лежащих на оси Ог. При этом условии общеизвестные [1–4] теоремы и приёмы их доказательства для уравнения (1) «работают» только для областей, границы которых не имеют точек на оси Ог.

Заметим, что ситуация «типична» для осесимметричных процессов, описываемых уравнениями эллиптического типа. И это несмотря на то, что исследуемые параметры являются непрерывными. Действительно, лапласиан в цилиндрической системе координат для осесимметричных процессов всегда включает в себя слагаемое, аналогичное слагаемому 7^7 в уравнении (1). Поэтому как раз при исследовании процессов с непрерывными физическими параметрами коэффициент при ^7 будет неограничен.

Работа [1] опубликована более полувека назад. Несмотря на преклонный возраст, эта книга по-прежнему представляет собой содержательный обзор теории эллиптических уравнений с частными производными. В этой работе принцип максимума доказан только при условии ограниченности коэффициентов при первых производных.

В доступной литературе отсутствует формулировка и доказательство принципа максимума для случая неограниченных коэффициентов при первых производных. Как показано выше, такая теорема востребована, по крайней мере, при изучении осесимметричных процессов. В данной работе предпринята попытка устранить указанный пробел. В осесимметричных процессах, как правило, коэффициент при производной в осевом направлении ограничен. В приведенном выше примере это коэффициент при ^^ 7 . Этого оказывается достаточно для верности принципа максимума. Полученные в работе утверждения могут быть применены не только для уравнений, записанных в цилиндрической системе координат т,р,к. Поэтому используются традиционные для математического анализа переменные

Ж, у, 2.

• 2.    Вариант принципа максимума

Теорема 1. Пусть функция п (х,у) € С2 (G) QC (G), где область G С R2 ограничена, а уравнение

1^1 +   п = ° ( ж, у) 1г^п + ^b ( ж, у) 1т^п

ох2 оу2           ох          оу выполнено во всех точках G. И пусть хотя бы одна из функций а (х, у) или b (х, у) ограничена на множестве точек области G. Тогда максимум функции п (х, у) в замкнутой области G достигается на границе dG = G\G.

Замечание. Отметим, что в теореме не затрагиваются вопросы существования или единственности решения уравнения (2), а описывается свойство какого-либо решения п (х,у), если последнее существует.

Доказательство. Пусть, для определённости, ограничена функция b (х.у). Тогда для некоторого числа В >  0 в области G выполняется неравенство | b (х,у) | <  В.

Доказательство проведём методом от противного. Функция п (х, у) непрерывна на компактах G и dG. Поэтому существуют оба максимума: М = max g { п (х,у) } и т = max gy {п (х, у) } . Допустим, что выполняется неравенство М > т и назовем это допущение главным допущением. Из него следует существование точки (х о ,у о ) € G такой, что п (х о ,у о ) = М .

Обозначим

L = max_ { у }- min_ { у } ( ж,у ) е с          ( ж,у ) е с

(L — габаритный размер замкнутой области G вдоль оси Оу) и

^шп^а}.

Рассмотрим множество G a = G Q П - пересечение замкнутой области G и полосы шириной A

П = { (х, у) : а < х <  + го , у о <  у <  у о + A } .

Граничные точки этого множества могут лежать только на двух прямых линиях у = у о , у = у о + A и на границе замкнутой области G. Возможны два случая (рис. 1). Первый случай — max^^ g { у } <  у о + A. Второй случай — max^^ g { у } > у о + A.

В первом случае рассмотрим на множестве G^ вспомогательную функцию пі (х,у) = п (х,у) +

М — т 2L ²

⁽ у ^— у о ^{) 2} .

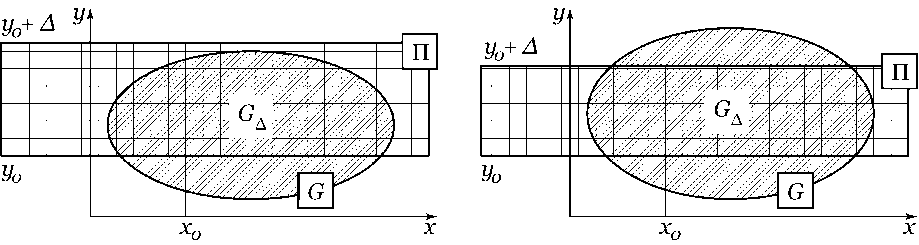
a)                                                      б)

Рис. 1. а) max _(a. ,_{y )G(5} {у} < у д + ^А , б) ^тах (_ж,_у)е<3 {У } > У о ^{+ А}

Возможна ситуация, при которой число ni (xq, уо) = М окажется максимальным значением функции ni на множестве G-. Тогда в точке (xq , уо) будут выполнены условия д2        д2        д        д

_дХ 2 ^и 1 <  0, _д- ₂ n i <  0, ^n i = 0, —n i = 0.

Последние два условия будут выполнены, поскольку д , х Э ,       , д , д 9 ,

^« i ( xq , У о ) = —n ( xq , У о ) = 0, — n i ( xq , У о ) = —n ( xq , у о ) = 0.

Рассмотрим поведение функции n _i (х,у) на разных частях границы множества G _— . В точках границы, лежащих на прямой у = у о , выполняется равенство n _i = n, поэтому n _i = n <  n ( xq , у о ) = М . В силу условия тах (_ж^ _е £ {у } <  у о + А все остальные точки границы G — являются граничными точками замкнутой области G. Поэтому в этих точках ²

согласно основному допущению и неравенству ^2 < 1 имеем ni = n +  —2А (у - Уо)2 <т + --^А А2 < т + М - т = М.

Таким образом, вспомогательная функция n _i подобрана так, что во всех точках границы множества G - величина n _i не превосходит числа М . Поэтому в ситуации, когда значение n _i в точке ( xq , у о ) не является максимумом функции n _i на множестве G - , максимум n _i будет достигаться во внутренней точке множества G - . В такой точке условия (3) также будут выполнены. Поэтому в обеих ситуациях существует точка ( xQ , у * ) € G - Q G, в которой выполнены условия (3).

Подставив выражение n = n _i — ^2^—Г (у — у о ) ² в уравнение (2), получим уравнение для вспомогательной функции n i :

+       = а (х,у) ^-n i + b (х,у) ^-n i — b (х,у) ^М ₂ ^А (у — у о ) + ^М - ^А .

дх ²     ду ²             дх           ду              L ²                L ²

В точке ( xQ , у * ) из этого уравнения, с учетом условий (3), получим неравенство

^М _{— 2} ^{А ( —b ( х} , у) ⁽у *

^— У о ) ⁺ 1) <  ⁰,

или

¹ <  ⁽у * ^— у о ) ^{b (}Х, у).                                          ⁽⁴⁾

Однако значение А выбрано так, что выполняется неравенство | (у * — у о ) b (х,у ) | <  А •В <  2 , которое противоречит неравенству (4). Полученное противоречие показывает, что в рамках главного допущения случай max ^ ^,^ ) _Eq { у } <  у ₀ + А невозможен.

Рассмотрим теперь второй случай, т.е. случай max^ y^g { у } > у д + А. Докажем сначала, что существует точка (ж і ,у д + А) G G, в которой функция и принимает значение М . Допустим, что это не так, т.е. выполняется неравенство М > т у ₀ +д , где т у ₀ +д = max g р{ у _{= $/0} +д } { и } (максимум существует, т.к. функция и (ж, у) непрерывна на компакте G Q {у = у д + А } ).

Обозначим т1 = max {т, тУ0+д} .

Рассуждая, как и в случае max ^ , y ) _e g {у} — у д + А, приходим к выводу, что существует точка (ж д ,у д ) G G д QG, в которой выполнены условия (3) для вспомогательной функции и 1 = и + ^ l ™ ¹ ( у - у о ) 2 . Как и выше, учёт того, что функция и = и 1 — ^ l ™ ¹ ( у - уо ) ² УДовлетворяет уравнению (2), приводит к неравенству (4). А это вновь противоречит выбору А. Полученное противоречие доказывает, что в случае max - , y ) _e g { у } >  уо + А существует точка (ж і , у д + А) G G такая, что выполняется равенство и (ж і , у д + А) = М .

Повторим проведенное доказательство, взяв вместо точки (ж д ,у д ) точку (ж і ,у д + А). В результате получим, что существует точка (ж2,у д + 2А) G G, в которой выполнено равенство и (ж2,у д + 2А) = М . И так далее. Через некоторое количество шагов к окажется, что существует точка (ж ^ , у д + кА) G G такая, что и (ж ^ , у д + кА) = М , и при этом будет выполнено неравенство max - , y ) e G { у } — уо + кА + А. Выше этот случай назван первым случаем (рис. 1) и разобран в начале доказательства. Показано, что этот случай невозможен в рамках главного допущения. Таким образом, главное допущение приводит к противоречию. Теорема 1 доказана.

Следствие 1.1. В условиях теоремы функция и (ж, у) достигает своего наименьшего в замкнутой области G значения на границе dG.

Доказательство. Как обычно [1–4], доказательство сводится к рассмотрению функции w (ж,у) = —и (ж,у).

Следствие 1.2. Пусть функция и (ж, у) непрерывна на замыкании G ограниченной области G С R ² , а уравнение

^-^и + 1Г9^и = а (ж, у, и) ^-и + b (ж, у, и) ^-и

Уж2    ду2             Уж            оу выполнено во всех точках G. Пусть хотя бы одна из функций а (ж, у, и (ж, у)) или b (ж, у, и (ж, у)) ограничена на множестве точек области G. Тогда минимум и максимум функции и (ж, у) в замкнутой области G достигаются на границе dG.

Доказательство. Так как рассматривается некоторое фиксированное решение и (ж, у) уравнения, то условия доказанной выше теоремы 1 будут выполнены, если в качестве а (ж, у) и b (ж, у) взять а (ж, у, и (ж, у)) и b (ж, у, и (ж, у)), соответственно. В этом случае теорема 1 и следствие 1.1 обосновывают верность следствия 1.2.

Для практического использования следствия 1.2 заметим, что если, например, функция а (ж, у, г) является непрерывной функцией своих аргументов на G х [ —то , + то ], то из условия непрерывности и (ж, у) на G, следует ограниченность а (ж, у, и (ж, у)) на G.

• 3.    Пример применения

• 4.    Многомерный случай

• 5.    Заключение

Во введении было сказано, что общеизвестные [1–4] теоремы и приёмы их доказательства для уравнения (1) «работают» только для областей, границы которых не имеют точек на оси Ог. Для применения теоремы 1 учтем, что внутренние точки любой области G, лежащей в радиально-осевой полуплоскости, не лежат на оси Ог. Поэтому коэффициенты уравнения (1) определены во всех точках области G. Коэффициент при |І7, а именно, Vz ограничен в любой ограниченной области в силу предположения о ламинарности течения. Поэтому выполнены все условия теоремы 1 и допускается, чтобы граничные точки G лежали на оси Ог. В результате получается принцип максимума произведения окружной скорости на радиус: пусть осесимметричное ламинарное течение несжимаемой жидкости с ненулевой вязкостью установилось в отсутствие внешних массовых сил и пусть G — произвольная ограниченная замкнутая область, лежащая в радиально-осевой полуплоскости г > 0; тогда минимум и максимум произведения окружной скорости на радиус достигаются на границе области G.

Доказательство теоремы 1 и её следствий, проведенное выше для двухмерного случая, легко может быть повторено в многомерном случае. Как и в двухмерном случае, в доказательстве потребуется, чтобы коэффициент при частной производной по одной из координат был ограничен. Представляется излишним приводить такое доказательство и давать громоздкую формулировку для случая произвольной размерности. Ограничимся формулировкой соответствующей теоремы (аналога следствия 1.2) в пространстве размерности три.

Теорема 2. Пусть функция и (x,у,z') непрерывна на замыкании G ограниченной области G С R3, а уравнение д2      д2      д2

дх2 и + ду2и + dZ2и = ддд

= а (х, у, z, и(х, у, z)) —и + b (х, у, z, и(х, у, z)) —и + с (х, у, z, и(х, у, z )) —и     (5)

выполнено во всех точках G. Пусть хотя бы одна из функций a(x,у,z,и), b (x,у,z,и) или с (х, у, z, и) ограничена на множестве точек области G. Тогда минимум и максимум функции и (х, у, z) в замкнутой области G достигаются на границе дG.

В работе исследованы линейные относительно частных производных уравнения эллиптического типа с неограниченными коэффициентами при первых производных. На примере двухмерного уравнения доказана теорема о достаточном условии того, чтобы решение подчинялось принципу максимума. Это условие ограниченности хотя бы одного из коэффициентов при первых производных. Из этого, в частности, следует «практическое» правило: решение будет подчиняться принципу максимума, если есть возможность развернуть прямоугольную систему координат так, чтобы хотя бы один из коэффициентов при первых производных в уравнении (5) оказался ограниченным в рассматриваемой области.

Результат может быть использован при качественном анализе физико-химических и биологических процессов, а также для априорных и для неинвазивных оценок.