Принцип обратимости в униполярных машинах Фарадея

Электрические униполярные машины, прообразом которых послужил генератор Фарадея, имеют широкую область применения и изготавливаются многими крупными фирмами. Естественно, имеется и методика расчета [1]. Вместе с тем научная обоснованность этой методики, а, проще говоря, общепризнанное объяснение принципа действия этого генератора отсутствует.

Казалось бы, для объяснения генератора проще всего воспользоваться принципом обратимости электрических машин и использовать принцип действия двигателя Фарадея. Но проблема в том, что и этот принцип плохо обоснован (и доказательством этого служит как раз невозможность "инвертировать" его в применении к генератору).

Ниже используется объяснение принципа действия двигателя Фарадея, данное в [2], и показывается, что аналогичный подход можно использовать для объяснения принципа действия генератора Фарадея.

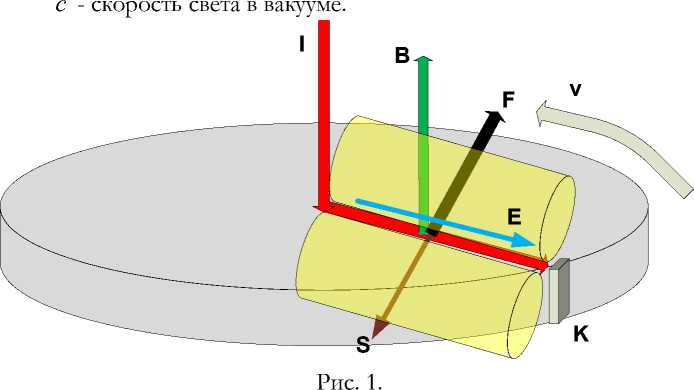
В двигателе Фарадея (см. рис. 1) имеется электропроводящий магнит с индукцией B , линия тока I , проходящего по оси вращения, радиусу магнита и неподвижный контакт K. На токопроводящем радиусе имеется электрическая напряженность

E = jp.                                              (1)

где j - плотность тока, p - удельное сопротивление. Магнитная напряженность H пропорциональна индукции B . Векторы этих напряженностей взаимно перпендикулярны и поэтому возникает поток электромагнитной энергии с плотностью

5 = EH .                                          (2)

Заметим, что этот поток возникает в статическом электромагнитном поле. Поток статического поля замкнут (из-за закона сохранения энергии) и поэтому показан на рис. 1 цилиндрами. Радиус магнита, по которому течет ток I , является линией соприкосновения этих цилиндров. Вектор потока 5 , лежащий на поверхности магнита, перпендикулярен указанному радиусу. Этот поток 5 создает силу F , направленую противоположно вектору потока 5 , и вращающую магнит со скоростью v . Эта сила является силой Хмельника [2] и вычисляется по формуле

F = V • 5 • ^ём!c ,                                   (3)

где

• 5 - плотность потока энергии,

• V - объем тела, пронизываемого потоком электромагнитного поля,

8 - относительная диэлектрическая проницаемость магнита, точнее, той его части, по которой протекает ток ,

М - относительная магнитная проницаемость магнита,

В [3] показано, что диэлектрическая проницаемость проводника с током зависит только от ц и р :

£ =

с л²

H

V р )

ц.

где цо - магнитная проницаемость вакуума, р - удельное сопротивление проводника. Объединяя (1, 3, 4), получаем

F = VjB ,                                             (5)

где j - плотность тока, B - магнитная идукция. или

F = IBL ,                                           (6)

где

I - ток,

L - длина радиуса.

Формально эта формула совпадает с формулой силы Ампера, но только формально, т.к. здесь сила приложена к магниту.

Например , при B = 1 [ ^ 1 j = 4 [ a / sm ² ] = 4 - 10⁴ A / m ² ] из (5) находим, что F [ N ] = 4 • 10⁴ V [ m ³] . В частности, при V = 10 ^{- 3}[ m ³] находим, что F = 40[ N ] .

Обозначим:

U - напряжение источника,

R - общее сопротивление,

L - длина радиуса, l = L/2 - средний радиус приложения силы, J - момент инерции, to - скорость вращения, v = tol = toL]2 - средняя линейная скорость, PH - мощность нагрузки двигателя.

M H - момент нагрузки.

По закону сохранения момента импульса имеем: d ω

J --= Fl - M_H . dt           ^H

Следовательно, d^ = (FL-2 - Mh ) J. dt (8) Мощность, развиваемая силой F , PF = vF = toFL/ 2 (9) или, с учетом (6), PF = roIBL]2. (10) Уравнение баланса мощности имеет вид: UI = I1 R + P . F (11) или U = IR + e, (12) где e = BtoL2/2, (13) т.е. двигатель Фаралея создает для источника напряжения противо-э.д.с. Таким образом, в проводнике, движущемся в неподвижном магнитном поле, создается э.д.с. В нашем случае проводник движется вместе с источником магнитного поля. Но и в этом случае в нем должна создаваться э.д.с., т.к. магнитное поле не перемещается вместе с объектом, его создающим.

Из (12) имеем:

, U - e

I = D ,                                                     (14)

R

Из (6, 8) имеем:

d^ = (!BL42 - M h ) J .                        (15)

Очевидно,

P H = Мн ю .                                       (16)

Приведенные уравнения (13-16) позволяют найти все

неизвестные, как функции времени, при ю (0) = 0 - см. рис. 2 при

L=0.2, J=0.02, R=0.5, U=5.9, B=1, Mh=0.2 в системе СИ.

В установившемся режиме

I = 2 Mh/BL 2,(17)

e = U - IR ,(18)

ю = 2e/BL2.(19)

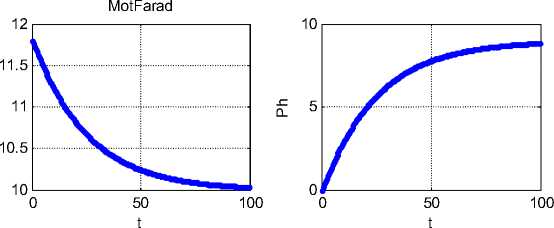
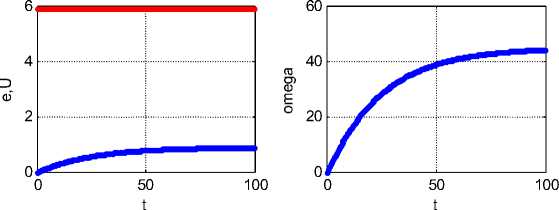
Рис. 2.

Совмещая уравнения (13-15), найдем:

d ω dt

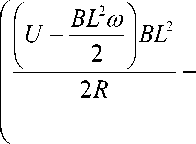
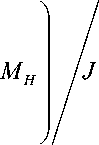
или

d ω dt

- a to + d, b = BL2, a =

b ²   , 2 bU - 4 RM

----, d =------------ 4 RJ        4 RJ

Следовательно, to =—(1 - exp(-at)), a

ω max

d a

2 bU - 4 RM H b ²

и длительность разгона

3 12 RJ a_ ь 2

(22а)

3. Моделирование генератора Фарадея

Для моделирования генератора Фарадея воспользуемся принципом обратимости электрических машин.

Предположим, что в генераторе тоже существует сила F вида (6). В начальный момент она может появиться как результат возникновения тока, вызванного силой Лоренца – в этом случае она должна иметь очень незначительную величину, поскольку эксперименетально такой ток не обнаруживается.

Обозначим момент двигателя и момент силы F как M_D , M_F . Тогда

M F « FL /2 = IBL^2 .                      (3 1 )

Мощность, развиваемая силой F , определена по (10), а мощность двигателя

P D = M d ® (32)

Используя принцип обратимости электрических машин, запишем по аналогии (20) уравнеие закона сохранения момента импульса для генератора:

Jd ® = P D - M F . dt ω	(33)
Следовательно,
d ® = f P D - M F ) Jj. dt V ®      //	(34)
Уравнение баланса мощности имеет вид:
P D = 1 2 R + P f .	(35)

Из (10, 35) находим:

P D = 1 2 R + a IBL/1
или	Iг R + el - P D = 0 .	(36)
где	e = ® BL 2/2 .	(37)
Эта формула совпадает с формулой (13) для двигателя		и с
формулой Тамма	[4], полученной иначе. Из (36) следует,	что
генератор Фаралея	является источником тока
	। _ - e + ee 2 + 4 RP D 2 R        ,	(38)

Напряжение на генераторе

U = IR .	(39)
Электрическая мощность генератора P = UI = 1 2 R .	(40)
Из (34, 31) находим: — = f P D - IBL^2 ) J J .	(41)
dt V to           )[ В установившемся режиме находим из (41): | P D - IBL 2/2 | = 0. V to              )	(42)

Следовательно, если двигатель вырабатывает мощность P_D при скорости ω , то ток генератора

I = 2 P D / to BL ².                                  (43)

Приведенные уравнения (37-41) позволяют найти все неизвестные, как функции времени, при данных начальных условиях I ( 0 ) = 0, to (0) = to o - см. рис. 3 при to o = 10 , J=0.02, L=0.2, R=0.5, B=1, P D =11, to max = 50 в системе СИ. Функции на рис. 3, указанные слева от окон, перечислены в соответствии с графиками сверху вниз; в скобках указан цвет линии.

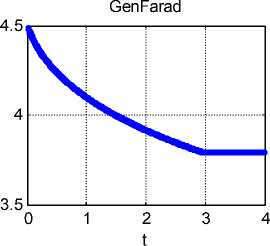
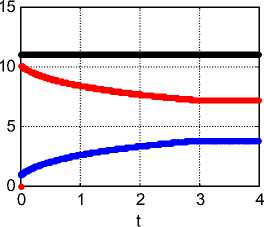
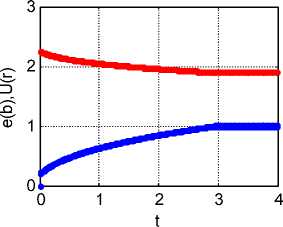
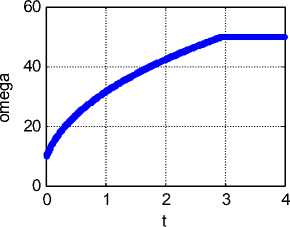
Рис. 3.

Решение этих уравнений существует при данных начальных условиях I ( 0 ) = 0, to (0) = to o . Следовательно, если в некоторый момент при вращении возникнет ток I , то через некоторое время он резко возрастет, а в дальнейшем начнет уменьшаться вместе с увеличением скорости вращения ω . При стабилизации скорости ® = to max двигателя (вращающего генератор) ток I генератора примет значение (43).

Начальный скачок тока может быть обеспечен (как уже говорилось) силой Лоренца. При этом сила F должна возникнуть как следствие закона сохранения момента импульса.