Принципы ab initio в моделировании газоподобных наносистем из молекул и пустоты

Пустота в данной работе представлена как обязательный компонент наносборки молекул в газе.

Основные термины: наносистема, наносборка и пустота . Термин «нано…» указывает на объект, размер которого является базовым фактором исследования. Нанораз-мерный объект в веществе, изделии или иной структуре составляет в каждом из трех измерений от 1 до 100 нм. В рамках этого соглашения нанообъект, например, в атомной структуре кристалла может составить от 27 до 27 000 атомов, если условно их расположить на расстоянии 1/3 нм друг от друга [7]. Группы из такого количества атомов можно называть кристаллическими нанофрагментами, когда они разграничены между собой условно, или наночастицами, когда они имеют отчетливо выраженную границу с окружающей средой. Объект с линейным размером менее 1 нм обычно называют кластером . Атомная частица имеет линейный размер от 0,1 до 0,3 нм. Различные системы радиусов атомных частиц составили важнейшие разделы молекулярной физики, минералогии, кристаллохимии и кристаллографии, квантовой физики и химии. Объекты с линейным размером более, чем атом, кластер или ассоциат, в газе не рассматривались. Ниже показано, что в газе можно выделить объект из молекул и пустоты размером 3 нм и более в зависимости от плотности вещества.

Наносистема в иерархии тела . Конституция вещества определяется не только соотношением размеров атомов, но также их количеством. Химическая связь объединяет атомы так, что их сцепка может быть бесконечно большой. Примером служит кристалл. Сцепка из 2–10 атомов имеет размер меньше 1 нм. Тогда сборка атомарных сцепок силами слабее химических может составить нанообъект. Энергия связи частей такой наносборки меньше, чем у молекул и наночастиц, поэтому устойчивость наносборки достигается действием внешней силы, источником которой может служить окружающая среда. Примерами действия окружающей среды на результат наносборки служат мицеллы в коллоидных растворах или кластеры в аэрозолях. Наносборки молекул с окружающей средой теперь принято называть наносистемой.

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 9

Пустота и атомы . Стабилизирующим компонентом газоподобных наносистем может служить пустота. Формулировка физической сущности пустоты нами в литературе не найдена. Здесь под пустотой понимается часть пространства вещества как антитеза атомам тела. Пустота реальна, как атомы и молекулы: например, будет справедливым утверждение, что на пустоту в воздухе приходится 99,9% объема.

Пустота, соударения и ассоциация . Пустота обеспечивает всем молекулам любой газоподобной наносистемы сближение и соударения в поступательном движении. Между молекулами существуют силы с действием 1 нм и более (Ван-дер-Ваальс, 1869 г.). Когда в конфигурации скрещивающихся траекторий можно построить перпендикуляр такой длины, тогда во время сближения молекул возможно формирование нанообъекта, кинетическая энергия которого превышает потенциальную, время жизни ограничено микросекундой. Такое взаимодействие молекул принято называть ассоциацией, с тем чтобы отличить сближение и удаление молекул по скрещивающимся траекториям от сближения, соударения и удаления молекул по пересекающимся траекториям. Формулировка явлений ассоциации и соударения атомов автором в литературе не найдена.

Пустота и наносборка . Традиционные понятия об ассоциации и соударении молекул не включает пустоту газа как участницу этих событий, поэтому наносборка из частиц и пустоты – более общее явление, чем ассоциация и соударение молекул.

Понятие о наносборке из молекул в сочетании с пустотой позволило получить новые данные о конституции газа и жидкости. Изложенные выше обстоятельства привели нас к выводу, что предлагаемая модель газа является качественно новой (см. далее).

Принципы ab initio в модели газа из пустоты и атомов

Постановка задачи . Соударения и ассоциацию молекул описывают методами статистической физики и термодинамики. Последовательный учет двойных, тройных, четверных и большего числа столкновений позволяет решить лишь геометрический аспект дальнего взаимодействия: коллективное взаимодействие в этом случае учтено не в полной мере [9]. Задача окончательно не решена, поэтому мы обращаем здесь внимание на истоки атомно-молекулярной гипотезы и кинетической теории, с тем чтобы найти согласие между законом Авогадро и уравнением состояния газа как новый аспект ближнего и дальнего взаимодействия в коллективе молекул.

В данной работе к такому традиционному принципу ab initio построения вещества, как атомно-молекулярная теория, нами добавлена пустота как неотъемлемая часть физического тела. Пустота обеспечивает атому и молекуле движение.

Атомы или молекулы в пустоте трактуются здесь как тело, устойчивость которого достигается взаимодействием частиц. Масса частиц обуславливает механическое взаимодействие; электромагнитное взаимодействие обеспечивается конституцией частиц.

Объединим в газе атомы или молекулы. Возникшее коллективное взаимодействие частиц построим на атомно-молекулярном и кинетическом принципах ab initio и следующих из них положениях нашей модели газа.

Частицы газа . Графика частиц газа. В излагаемой модели пустота и частицы составляют физическое тело. В графике тела пустота служит фоном для изображения частиц в виде геометрической фигуры – сферы или точки.

10 в ыпуск 2/2019

Химическая индивидуальность в графике частиц газа. Точечная частица в нашей модели не имеет структуры, поэтому она не обладает химической индивидуальностью. Точка как геометрический символ подчеркивает также изолированность частицы от других.

Носителем химической индивидуальности является атом. Атомы объединяются в молекулы. Атом и молекула являются частицами со структурой. В газе они представлены условно сферой, с тем чтобы подчеркнуть это качество. Сфера как геометрический символ сохраняется вне зависимости от связи атома или молекулы со средой и остальными частицами: сферическая частица является в нашей модели также символом химической индивидуальности.

Размерность частиц газа. Точечная, или условно-сферическая, частица является приближенным отражением реальности: структура атома или молекулы не может быть отображена в точке, а сфера лишь фиксирует ее наличие. Поэтому в газе условно-сферическая частица отнесена нами к размерному объекту, однако точечная частица безразмерна.

Единичное состояние частицы. Мерой регулярности положений частиц считают расстояние между ними. В газе положение частицы нерегулярно. Функция времени и координат частиц иллюстрирует корреляцию их положений. Ее непрерывность позволяет выделить в нашей модели положение частицы со средним удалением от других и считать его единичным. Подчеркнуть, что единичные состояния частиц не изолированы друг от друга, можно терминами «единичная частица» или «единичный атом или молекула». Кристалл и разреженный газ являются примером комбинации единичных частиц. В плотном газе количество единичных частиц переменно при постоянном количестве атомов или молекул. Отношение их количеств является одним из искомых решений моделирования нанообъектов в газе.

Движение частиц . В излагаемой модели газа движение атомов и молекул разделено на два вида: инерциальное и неинерциальное. Каждое из них вводится специальным способом.

Источником первого вида движения является пустота, которая обеспечивает частицам поступательное движение. Пустота неотъемлема от частиц как среда для них. В кинетической теории атрибутом инерциального движения является длина свободного пробега [11], введенная Дж. Максвеллом в 1859 г. Упругое соударение частиц – это предельное проявление инерциального движения.

Источником второго вида движения служат силы, которые вводятся в вещество извне и не вызывают инерциального движения. К ним относятся сила из классической механики, термостат из статики, заряды и токи из электродинамики. В отличие от пустоты эти источники движения преходящи: они возникают и исчезают, например, за время сближения и отдаления частиц газа.

В нашей модели движение частицы может быть комбинированным – ассоциация молекул, например, является его результатом. Неупругое соударение частиц представляет собой предельное проявление комбинационного движения.

Замкнутые и протяженные объекты в газе . Инерционное движение частица совершает без приложения силы. После приложения силы она совершает комбинационное движение, включающее как инерционное, так и неинерционное движения. Мы вправе

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 11

считать сферическую частицу материальной точкой приложения силы [11, с. 122]. Справедливо обратное утверждение, которое в данной модели использовано так, чтобы материальную точку приложения силы представить в виде группы сферических частиц, т.е. замкнутых и протяженных объектов.

Замкнутый объект. Поместим, например, две или три материальные точки в пустоту, с тем чтобы придать им инерциальное движение, выделим их сферой. Сведем к центру сферы векторы скоростей и составим общий импульс. Поток общего импульса через сферу возникает под действием внешней силы на движение материальных точек. Когда движение материальных точек не влияет на инвариантность общего импульса, мы вправе трактовать изменение общего импульса как движение сферы, т.е. замкнутого объекта из нескольких материальных точек.

Протяженный объект. Нерегулярность положений условно сферических частиц в пустоте позволяет выделить в графике частиц обособленную группу из двух, трех или более частиц. Опишем ее замкнутой поверхностью, определим центр их масс. Сведем к нему векторы скоростей и введем в рассмотрение силу, возникающую от движения зарядов внутри частицы и сферы. Составим общий импульс. Можно утверждать, что поток импульса через выделенное замкнутое пространство возникает и исчезает за счет вхождения, сближения и удаления частиц.

Выбрав поток импульса как критерий сравнения обособленной группы частиц и описанного выше замкнутого объекта из материальных точек и сферы, можно рассматривать движение в пустоте группы сближающихся и разлетающихся частиц как движение протяженного объекта из частиц, ограниченного сферой. Граница протяженного объекта произвольна, линейный размер определяется расстоянием между частицами. Протяженность объекта является одним из искомых решений моделирования нанообъектов в газе.

Протяженная частица в газе. Протяженность объекта из частиц зависит от тех физических условий, в которые попадают сферические частицы [1]. К протяженным объектам в газе можно отнести молекулярные ассоциаты, кластеры и наносборки. В нашей модели протяженные объекты отличаются от вышеперечисленных протяженных объектов. Объект из более чем одной частицы мы идентифицируем как «протяженную частицу», как антитезу термину «единичный атом или молекула».

Время жизни протяженной частицы ограничено временем действия внешней силы, т.е. отрезком времени от возникновения до завершения молекулой комбинационного движения. Необходимость в протяженных частицах вызвана тем, что их количество в газе варьируется при постоянном количестве молекул газа. Расчет количества протяженных частиц как функции давления и температуры является одной из задач моделирования нанообъектов в газе.

Ближнее и дальнее взаимодействие частиц . Близкие взаимодействия возникают на расстояниях меньших, чем среднее расстояние между частицами. Превышают указанную величину дальние взаимодействия. Среднее расстояние между частицами газа меньше средней длины свободного пробега, поэтому в газе возможны близкие и дальние взаимодействия.

Представление о единичной и протяженной частицах газа в излагаемой модели позволяет описывать ближнее и дальнее взаимодействия, избегая расчета среднего и мгновенного расстояний между молекулами, длины свободного пробега. Возникновение

12 в ыпуск 2/2019

протяженной частицы из единичных частиц и ее распад относятся нами к ближнему взаимодействию. Дальнее взаимодействие в нашей модели газа возникает, когда единичная частица участвует параллельно в образовании двух, трех и более протяженных частиц.

Представления о соударениях достаточны для описания ближнего взаимодействия в совокупности молекул. Метод двойных столкновений устанавливает равномерность распределения частиц в объеме газообразного тела, поэтому при одинаковых температуре и давлении число частиц в единице объема одинаково независимо от природы газа [11, с. 158]. Равномерность распределения энергий частиц в объеме газообразного тела должна быть результатом и дальнего взаимодействия. Поскольку число протяженных частиц зависит от давления и температуры, распределения частиц по скоростям и энергиям как их функции характеризуют и ближнее, и дальнее взаимодействия частиц газа.

История и современное состояние вопроса о пустоте

Пустота является тем атрибутом физического тела, которое вводит в нашей модели поступательное движение частиц газа по инерции. Инерциальное движение введено в механику Г. Галилеем в 1633 г. [4, с. 282]. Экспериментальное доказательство пустоты состоялось в 1643 г. в опыте Э. Торричелли. Доказательство существования атома и молекулы состоялось в эксперименте Ж. Перрена в 1908 г.

С точки зрения античных ученых, если есть пустота, то в ней должны быть атомы. Справедливым для них было и обратное утверждение: без атомов нет пустоты [10]. Признание пустоты как философской категории совершилось в два этапа. Первый этап составило учение об атомах Левкиппа (V в. до н.э.), второй – учение Демокрита (V–IV вв. до н.э.). Пустота рассматривалась обоими философами как Небытие. Левкипп разделяет все сущее на множество элементов с помощью относительного Небытия так, что свойства элементов зависят от ограничивающего их Небытия. Демокрит снял это ограничение, утверждая, что среди Бытия находится Небытие, наполняя и пронизывая его. Известно его прозвище Пустодум (т.е. думающий о пустоте).

Платон признавал пространство третьим родом сущего. Его ученик Аристотель утверждал, что существование пустого пространства невозможно. Влияние Аристотеля на людей было столь велико, что две тысячи лет пустота была в их сознании мнимой категорией, и только в 1643 г. ее существование было подтверждено в опыте Э. Торричелли со ртутью и стеклянной трубкой. О. Герике в 1650 г. с помощью насоса получил в сосуде безвоздушное пространство. В 1679 г. И. Ньютон наполнил пустоту Демокрита неуловимым эфиром. В физике торжество пустоты над эфиром наступило в 1905 г. благодаря А. Эйнштейну и предопределило доказательство существования атома и молекулы.

Понимание инерциального движения, доказательство пустоты состоялось 400 лет назад. Доказательство существования атома и молекулы состоялось всего 110 лет назад. В современных вызовах науки нам нужно избежать тех ошибок в оценке роли пустоты, которые были допущены на долгом пути атомистики от Античности к современности. Примером служит вековой и драматичный путь признания заслуги Дж. Дальтона (1803) из-за его взгляда на атом без сопутствующей ему пустоты. В современной физике абсолютное ничто соответствует абсолютной пустоте.

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 13

Пустота и тело

Пустота как физическая категория тела . Бесконечная Вселенная не ограничивает пустоту. Пустота является тем атрибутом, который вводит во Вселенную частицы. Мысленно выделяя часть пустоты и наполняя ее статическими и динамическими сочетаниями атомов и молекул, получим тела от галактических и планетарных размеров до лабораторных.

В атоме или молекуле нет пустоты, поэтому конституцию тела можно характеризовать долями частиц и пустоты. Превалирование пустоты означает газовую конституцию тела. Напротив, превалирование частиц над пустотой приводит тело к конденсированному состоянию. В плотных шаровых упаковках на долю «пустоты» приходится до 30% объема.

Соизмеримость долей частиц и пустоты приводит тело в жидкое состояние. Существует особое состояние, в котором исчезает различие газа и жидкости. Поэтому соотношение пустоты и частиц в газе и жидкости указывает на общий уровень их иерархии – критическое состояние [13, с. 63], обнаруженное Д.И. Менделеевым в 1861 г. Согласно кинетической теории, в критическом состоянии вещества средняя длина свободного пробега молекулы соизмерима с ее радиусом. Когда молекулы в нашей модели утрачивают инерциальное движение, часть их приобретает другое качество, чем условно-сферические частицы, образуя протяженные частицы конденсата в контакте с паром. Отсутствие инерциального движения молекул в жидком теле обусловливает гомогенный характер его отвердевания и кристаллизации.

Для сравнения напомним, что в кинетической теории различие между твердыми, жидкими и газообразными телами можно видеть в вариации длины свободного пробега: для твердых тел она меньше радиуса молекулы, для жидкостей – равна радиусу, для газов – больше его [12, с. 56]. Этого объяснения недостаточно для описания агрегатных превращений, так как оно ошибочно обязывает тело совершить конденсацию или испарение по всему объему. Напротив, условие сохранения инерциального движения молекул позволяет объяснить гетерогенный характер конденсации и существование равновесия «жидкость – пар».

Иерархия газообразного тела . Пустота и частица составляют базовый уровень иерархии физического тела – его дисконтинуум. Конституция физического тела определяется не только энергией взаимодействия, размером и поляризацией атомов или молекул, но также их числом. Численный фактор важен в идентификации объектов для описания иерархии газообразного тела. В качестве объектов счета – структурных единиц – выбирают атом, молекулу, ассоциат или кластер. Каждая из перечисленных выше структурных единиц характеризует уровень иерархии газообразного тела.

Атомы отображают химический и стехиометрический состав молекулы. На этом уровне иерархии газообразного тела молекула представлена как точечная или единичная частица. Длительная дискуссия о базовой структурной единице газа закончилась разграничением на Международном съезде химиков в Карлсруэ (С. Канниццаро, 1861) понятий об атоме (Дж. Дальтон, 1803) и молекуле (А. Авогадро, 1811), согласно которому газ составлен из атомов или молекул, молекулы составлены из атомов [5]. Номенклатурным наследием этой дискуссии осталось «атомарное» название газа из молекул: водород, кислород, азот, другие двухатомные и многоатомные газы, например, пары серы S, S2, S4, S6 или S8.

14 в ыпуск 2/2019

Следующий уровень иерархии газообразного тела отображает закономерность относительного расположения атомов или молекул, которые составляют протяженные частицы – ассоциаты или кластеры. Молекулы могут составлять в газе димеры и полимеры. В отдельных случаях они могут рассматриваться как весьма устойчивые составные частицы. Так, димеры муравьиной и уксусной кислот характерны и для газовой фазы. Результатом статистических сочетаний молекул, атомов и ассоциатов являются кластеры. Размеры димера и кластера позволяют рассматривать их как элемент наносистемы и предмет наносборки.

Газ как физическое тело не имеет определенной формы. Газообразное тело отображает воздействие внешней среды на геометрию тела. Тяготение формирует тело галактического газа, совершающего поступательное, вращательное и колебательное движение. В планетарном масштабе геометрию тела формируют тяготение и форма Земли. В лабораторном масштабе тяготение мало и геометрию тела формирует контакт газа с конденсированным веществом.

Ранние модели газа

Физический аспект ранних моделей газа . Первая модель газа не выходит из сферы абстракции и связана с именем Р. Бойля. Он заимствовал у древних философов идею абсолютно пустого пространства и универсальной материи со свойством формы, величины и движением [5]. В сочинениях 1661–1669 гг. Р. Бойль выделяет абсолютно неделимые частицы «minima», которые тверды и имеют определенную форму, составляют множество корпускул. Изменение свойств у видимого тела он рассматривал как результат движения корпускул. Газообразное состояние Бойль приписывал главным образом воздуху, состоящему из частиц самой разнообразной формы, что обусловливает его упругость.

Бойль не считал корпускулу весомой, иначе он бы предвосхитил работы Дальтона. Под частицей газа Дальтон понимал твердый шарик в центре шаровидной атмосферы-оболочки (рис. 1), объем которой может в 1000 и более раз превышать объем самого атома.

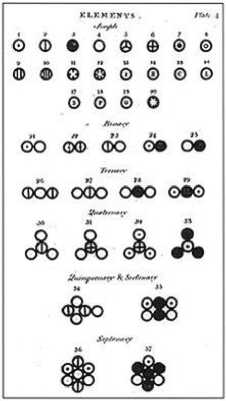
Рис. 1. Символы 37 простых и сложных атомов Дальтона (1808–1810): под номером 1 показан атом водорода, 3 – углерода, 4 – кислорода, 37 – сахара [5]

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем...

Частицы равны по объему и располагаются горизонтальными рядами. С их помощью Дальтон изобразил строение газов так, что шарики одной плоскости можно было ограничить линиями, которые составят геометрически правильные фигуры (рис. 2). Так как газы не являются угловатыми телами, Дальтон не стал соединять шарики черточками. Подчеркивая малую плотность газа в отношении кристалла, он выбрал символом кратности не геометрическую фигуру, а шарик-атом.

Рис. 2. Схемы Дальтона для водорода (1), окиси азота (2) и угольного ангидрида (3) [5]

Дальтон строил газ из атомов, между которыми действуют силы притяжения и отталкивания, имеющие всеобщий характер. Ошибаясь в источнике этих сил, он объяснял расширение и сжатие, нагревание и конденсацию результатом взаимного наложения этих сил. Ошибаясь в величине и весомости атомов, Дальтон объяснял диффузию газов и их абсорбцию жидкостями. Условие непрерывности вещества заставило Дальтона разместить шарики с оболочками по квадратам (рис. 3).

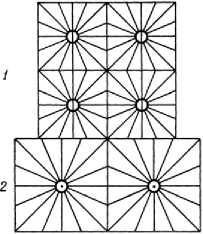
Рис. 3. Схема Дальтона для четырех частиц азота (1) и двух частиц водорода (2), объясняющая их взаимную диффузию [5]

Ошибаясь в регулярности расположения атомов в газе, Дальтон иллюстрирует открытый им закон кратных отношений объемов как соединение атома с атомом. Лучи, которые исходят из частицы газа, представляют упругую атмосферу. Они симметричны в квадратах (1), поэтому частицы азота могут образовывать механически равновесную систему. То же можно сказать о двух квадратах (2). Однако вместе частицы водорода и азота не могут составить равновесие; отсюда вывод о существовании внутреннего движения, всегда возникающего в смеси газов.

Модель газов Дальтона послужила стимулом к разработке атомно-молекулярной теории.

16 в ыпуск 2/2019

Математический аспект ранних моделей газа. Математические соотношения в ранних моделях газа просты. Бойль установил (1662) соотношение между давлением p и объемом V в виде pV = const.

Раскрытие физического содержания константы Бойля привело к установлению взаимосвязи между давлением и температурой ( p / Т = const, Ж. Шарль, 1787), объемом и температурой ( V / Т = const, Ж. Гей-Люссак, 1802). Эти соотношения стали достаточными для составления уравнения состояния газа. Первое уравнение состояния газа (Б. Клапейрон, 1834) содержало удельную газовую постоянную, индивидуальную для каждого газа.

Модель Дальтона вместе с гипотезой Авогадро (1811) позволили найти универсальное значение газовой постоянной. Закон кратных отношений Дальтона стимулировал Авога-дро в установлении отличия простых и сложных атомов Дальтона от молекулы. Дискуссия на эту тему выразилась в счете атомов и молекул.

В атомной модели Дальтона равные объемы газов при одинаковом давлении и температуре содержат одно и то же число атомов. В молекулярной гипотезе Авогадро равенство частиц относится к газам из молекул, которые составлены из атомов Дальтона. В атомной модели Й. Берцелиуса равенство частиц газов относится к числу атомов, составляющих молекулы. Справедливым оказалось утверждение Авогадро.

В настоящее время результат счета частиц выражается через физическую величину «количество вещества» и ее меру – моль. Принято, что число частиц в моле газа и других агрегатных состояниях любого вещества постоянно и равно величине N _А, названной постоянной Авогадро.

Постоянная Авогадро позволила Д.И. Менделееву вычислить универсальное значение R газовой постоянной [14, с. 288, 633, 653, 677] путем перехода от весомости частиц газа (массы вещества) к количеству частиц газа (1874). Уравнение для моля газа pV = RT (1)

включает только универсальную постоянную R . Очевидно, что законы Бойля, Шарля, Гей-Люссака представляют собой следствие уравнения (1).

В гипотезе Авогадро уравнение (1) имеет следующую физическую интерпретацию: равные объемы газообразных веществ при одинаковых давлении и температуре содержат одно и то же число молекул, так что плотность различных газов служит мерой массы их молекул и отношения объемов при соединении суть не что иное, как отношения между числом молекул, соединяющихся между собой при образовании сложной молекулы (Аво-гадро, 1814) [5, с. 184].

Заметим, что Бойль, так же как Дальтон и Авогадро, указывал на пропорциональность давления газа его плотности в изотермическом процессе. Поэтому уравнение (1) высвечивает справедливые утверждения корпускулярной и атомно-молекулярной гипотез. Так, математические соотношения в модели Бойля позволили утверждать, что газы разной химической природы могут находиться в одинаковых физических состояниях, которые могут быть достигнуты уравниванием двух параметров из трех: p, V и T . Выбрав давление и температуру в качестве независимых переменных, а объем как их функцию, Авогадро правильно сформулировал критерий равенства физических состояний газов:

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 17 равенство чисел молекул при равенстве двух независимых параметров, известное как закон Авогадро.

В дискуссии Дальтона и Авогадро параметры газа впервые были неявно классифицированы не только как независимые, но и как макро- и микроскопические, отнеся по этому признаку число частиц к внутреннему или микроскопическому параметру. Поэтому их дискуссию об атоме и молекуле можно интерпретировать как поиск корреляции макро-и микропараметров, в котором Авогадро был успешнее.

Ранние модели газа и гипотеза Авогадро все-таки не смогли дать теоретического обоснования уравнения состояния газа. Решение было найдено в кинетике большого числа молекул.

Кинетический аспект теории газа . Первое объяснение закона Бойля принадлежит Д. Бернулли, который в 1738 г. указал на внутреннее движение частиц как причину давления газа. Постоянное движение корпускул в пустоте составило основу модели Бойля, но обратная зависимость давления и объема, установленная в опытах (1660) и выраженная в форме уравнения (1), не получила объяснения из-за предположения о том, что притяжение и отталкивание корпускул зависят от их величины и формы.

Дальтон в газовой модели отказался от постоянного движения корпускул и пустоты как последователь теории флогистона. Однако он справедливо заменил корпускулу Бойля атомом, отказался от формы частицы как источника сил притяжения и отталкивания, связав форму и структуру частиц с химическим составом (см. рис. 1). Такая позиция Дальтона не противоречила теории флогистона, но и не привела его к отказу от идеи регулярности расположения атомов в газе.

Дальтон ошибочно расположил атомы в пространстве по законам симметрии решеток так, что между атомами не было пустоты (см. рис. 2). По его мнению, внутреннее движение в смеси разнородных атомов совершается вынужденно по причине неустойчивости комбинации из атомных оболочек-атмосфер, проистекающих из теории флогистона (см. рис. 3).

Дж. Герапат в 1820 г. отказался от модели регулярного расположения атомов и представил их в виде сталкивающихся шаров без каких-либо оболочек, т.е. упругих шаров. В новой модели шар стал постоянно двигаться с большой скоростью по отрезку прямой, была предложена зависимость произведения давления и объема от массы и скорости частицы, вычислены средняя скорость частиц (1832) и скорость звука, объяснены газовые законы и диффузия.

Однако в своей модели Дж. Герапат предложил считать, что импульс частицы задает температуру газа, или измерение импульса частиц является измерением температуры газа. Поэтому он хотя и предсказал существование абсолютного нуля температуры, но ошибся в квадратичной зависимости произведения давления и объема от температуры.

Удары частиц-шариков о стенки сосуда рассмотрел Дж. Джоуль в 1848 г. В 1856 г. Р. Клаузиус показал, что на давление газа влияют удары о стенку, а не соударения частиц. Вместе с А. Кренигом он обосновал уравнение состояния идеального газа, связав среднюю кинетическую энергию (а не импульс, как Герапат) с температурой. Крениг впервые предложил вероятностно-статистическое описание поведения молекул, сумел теоретически доказать закон Авогадро.

18 в ыпуск 2/2019

Максвелл осмыслил знания по физическим свойствам газа, накопленные коллегами ранее, и в 1859 г. вывел распределение молекул по скоростям, определил среднюю длину свободного пробега, средний диаметр частицы [1]. Международный конгресс химиков (Карлсруэ, 1860) по представлению С. Канниццаро внес ясность в понятия атома Дальтона и молекулы Авогадро, согласовал их конституцию в разных химических соединениях. Деление молекул стало одной из форм движения в молекулярной гипотезе Авогадро.

Исследования Л. Больцмана, Й. Ван-дер-Ваальса позволили перейти к расчету величины молекулы и их числа в единице объема. И.Й. Лошмидт вычислил количество молекул на единицу объема (1865). Превосходное совпадение полученных значений стало убедительным свидетельством реального количества молекул и справедливости молекулярно-кинетической теории. Опыт Ж. Перрена доказал существование молекул (1908).

Таким образом, из атомно-молекулярной гипотезы, с одной стороны, и гипотезы, согласно которой молекулы находятся в быстром движении, причем скорость этого движения возрастает с температурой, – с другой, трудами многих ученых была создана молекулярно-кинетическая теория газа, основные положения которой не утратили своих позиций и в настоящее время. Данная работа развивает эти положения. Ее предметом является существование систем из молекул и пустоты в газе. Автор не нашел в литературе работ, посвященных этой тематике, и считает роль наносистем в теории газа важнейшей.

Основные соотношения излагаемой модели

Закон Авогадро является необходимым следствием кинетической теории газа: в равных объемах различных газов, взятых при одинаковых температурах и давлениях, содержится одно и то же количество молекул. Закон Авогадро составляет существо современной физики и химии. В нашей модели он представлен в следующем виде.

• А.    Молекулы в количестве N ₀ составляют газ. В коллективе себе подобных молекула может менять качество в зависимости от физического состояния газа. Она может быть представлена в качестве точечной или единичной частицы или составлять протяженную частицу.

Б. Конституция газа определяется комбинацией молекул как точечных, единичных и протяженных частиц.

• 1.    Газ как комбинация из точечных и единичных частиц. Обозначим символом N ₁ количество единичных частиц. Величина N ₁ зависит от физического состояния газа. Так как количество исходных частиц N ₀ постоянно, отношение

• 2.    Газ как комбинация из единичных и протяженных частиц . Очевидно, что суммарное количество единичных и протяженных частиц N * зависит от физического состояния газа, выполняется условие N ₀ ≥ N *.

γ₁ ≡ N ₁ / N ₀                                   (2)

является мольной долей единичных (сферических) частиц в газе. Тогда выражение из количеств исходных ( N ₀) и единичных ( N ₁) частиц

γ_т ≡ ( N ₀– N ₁) / N ₀                               (3)

представляет собой в излагаемой модели мольную долю точечных частиц. Очевидно, что γ1 + γт = 1.

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 19

Величина N является известным параметром состояния газа, вычисляется через измерение плотности вещества. Величина N * не поддается ни прямому, ни косвенному счету. Для ее вычисления в нашей модели газа вводится искомая функция:

β ≡ N ₀ / N *. (4)

pV- кривая позволяет выразить зависимость величины β от давления и температуры, которая ниже раскрыта в рамках предлагаемой модели.

• В.    Выражения (2)–(4) являются основными соотношениями излагаемой модели. В отличие от давления, температуры и объема равные значения β и γ не означают равные физические состояния газа. Вычисление β и γ составляет первый этап моделирования газоподобных нанообъектов.

Примеры раскрытия величины γ и β. Закон Авогадро справедлив для частиц различной химической индивидуальности. Пусть N – количество исходных одинаковых частиц газа в виде много- или одноатомных молекул, N ₁ – количество единичных частиц, для которых выполняется условие N ₀≥ N ₁. Согласно выражению (2), мольная доля единичных частиц N ₁ / N ₀ в газе с точечными частицами лежит в интервале 0 ≤ γ₁ ≤ 1. Рассмотрим физические состояния газа, которые определяют вариацию значений γ₁.

Предельные значения γ₁ . Величина γ₁ имеет предельные значения: нижний предел γ = 0 отвечает условию N ≡ 0 верхний пределγ = 1 отвечает условию N ≡ N . Важно, что два предела указывают на два сорта газа: один из них составляют точечные частицы: γ₁ = 0 и γ_т = 1, другой – единичные частицы: γ₁ = 1 и γ_т = 0.

Точечная частица не обладает химической индивидуальностью, так как точка не обладает внутренней структурой. Атом или молекула как точечные частицы изолированы. В силу этого утверждения сближение и отдаление точечных частиц совершается без соударений. Примером служит форвакуумное состояние воздуха: γ = 0 и γ = 1.

Атом или молекула как единичные частицы не изолированы. Единичная частица может изображаться в нашей модели условно сферой, когда необходимо подчеркнуть существование ее внутренней структуры. В силу этого утверждения единичные частицы обладают химической индивидуальностью, которая проявляется в их сближении и разлете через соударения. Примером может служить воздух в нормальных условиях: ~ 5×109 столкновений молекулы за одну секунду, γ = 1 и γ = 0.

Значения γ₁ и γ_т идеального газа. В рамках термодинамики термин «идеальный газ» относится к гипотетическому состоянию вещества. Пределы величины γ указывают на два сорта газа: один из них составляют точечные частицы, другой – единичные. Предельные состояния газа можно считать гипотетическими, или идеальными.

Физическое состояние газа характеризуется плотностью: менее плотный газ, состояние которого можно считать гипотетическим, также выделяют как идеальный газ. Иные состояния газа называют реальными. Свойства идеального газа ранее не различали по сортам частиц. В нашей модели он разделен на два вида по количественному и качественному признакам: идеальный газ из точечных частиц, когда γ1 = 0 и γт = 1, или единичных частиц, когда γ1 = 1 и γт= 0. Их качественное различие состоит в том, что идеальный газ из точечных частиц не подчиняется уравнению (1): нет столкновений – закон Авогадро не выполняется [1, с. 158].

20 в ыпуск 2/2019

Значения γ смеси идеальных газов . Величина γ имеет предельные значения только для идеального газа. Идеальные газы, которые обладают химической индивидуальностью, могут составить смесь. В смеси все частицы единичны, но различаются по сортам. Пусть число и состав частиц идеального газа удовлетворяют равенству

N ₀ = N ₁₁ + N ₁₂.

Тогда для i -го сорта частиц выполняются условия: N ≠ N и γ ≠ 0, N ≠ N и γ ≠ 0 или 0 < γ _i < 1 и γ₁₁+ γ₁₂= 1.

Молекулярная наносборка в идеальном газе. Химическая индивидуальность единичных частиц позволяет образовать в идеальном газе устойчивую надмолекулярную структуру как сборку молекул. Примером может служить димер уксусной кислоты. Такую надмолекулярную частицу можно отнести к нанообъекту в идеальном газе: ее линейный размер превышает 1 нм.

Покажем, что для наносборок в идеальном газе должно выполняться условие 0 < γ < 1. Сборку молекул выразим через количество частиц до ( N ₀) и после ( N ) ассоциации, для чисел которых выполняется условие N ₀ ≥ N . Пусть в идеальном газе существуют димерные нанообъекты. Тогда число и состав частиц идеального газа удовлетворяют равенству

N = N ₁ + N ₂,                                (5)

где N – целое число, показывающее количество димерных частиц в газе. Общее число молекул до наносборок [2; 15]

N ₀ = N ₁ + 2 N ₂.                                (6)

Очевидно, что выполняются условия N 0 >  N >  N 1 . Поскольку в математическом аспекте две соприкасающиеся точки не являются протяженной фигурой, димерные нанообъекты N ₂ в идеальном газе также являются единичной частицей. Поэтому наносборка молекул идеального газа не является ни точечной, ни протяженной частицей: γ₁ = 1 и γ_т = 0.

Эффективность наносборки в идеальном газе в нашей модели можно характеризовать через сумму числа N ₁₁ мономерных молекул и числа N ₁₂ димеров. Поскольку после наносборок в идеальном газе нет ни точечных, ни протяженных частиц, то их сумма N = N ₁₁ + N ₁₂ и

η = N ₀ /( N ₁₁ + N ₁₂) = N ₀ / N .

Когда предметом моделирования является нанообъект в идеальном газе, вариации η и γ служат параметрами моделирования.

Реальный газ. Плотный газ, свойства которого не описываются уравнением (1), называют реальным. В нашей модели он составлен из единичных и протяженных частиц. Точечные частицы, как не участвующие в соударениях, отсутствуют. Значение 0 < γ₁< 1 для единичных частиц может быть вызвано ассоциацией или наносборкой одинаковых по химической индивидуальности частиц идеального газа, но разных по стабильности и составу частиц. В результате взаимодействия долю 1 – γ₁ единичных частиц образуют протяженные частицы.

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем...

Сборки молекул выражают через число частиц до ( N ) и после ( N ) их ассоциации. Пусть составы частиц удовлетворяют равенству

N = N + N + N +…+ N +…,(7)

где i – целое число, показывающее количество одинаковых частиц в группе. Для единичных частиц в газе i = 1. Значения i <  1 в сумме (7) указывают в нашей модели на протяженную группу из i частиц. Общее число молекул до ассоциации равно:

N0 = N1 + 2N2 + 3N3 +…+ iNi +… .(8)

N ₁ меньше N ₀. Доля единичных молекул равна γ₁ ≡ N ₁ / N ₀ и 0 < γ₁< 1. Тогда точечные частицы, доля которых 1 – γ₁ ≡ 1 – N ₁/ N ₀ составляют в газе протяженные группы. В статистической механике рассматривают группы не более пяти частиц [9].

Согласно равенству (7), величина N больше, чем N ₁. Согласно суммам (7), (8), ассоциаты и наносборки составляют только часть той доли γ-частиц, которые участвуют в сближениях и удалениях. Это обстоятельство указывает на то, что указанные суммы учитывают эффекты коллективного взаимодействия не в полной мере. Например, в них отсутствует учет надмолекулярных структур из частиц i -го сорта как результат дальнего взаимодействия. В нашей модели учет надмолекулярных структур представлен ниже уравнением (11) и величиной β из уравнений (4) и (12), для которых выполняется условие N ₀ > N ₁ >  N *, где N * – сумма единичных и протяженных частиц газа.

Закон Авогадро и уравнение состояния газа

Результаты изучения макроскопических параметров газа приводят в виде таблиц или в установлении уравнения состояния – соотношения между давлением p , объемом V и температурой T . Применения закона Авогадро к уравнению состояния в рамках молекулярной физики и термодинамики нами не найдено.

В установлении уравнения состояния массу газа принято считать постоянной. Удобно выражать ее через микроскопический параметр – сумму масс молекул, составляющих газ. Поэтому принято записывать уравнение состояния с постоянным числом N ₀ исходных молекул. Примером является уравнение (1).

Происхождение и сущность поправок в уравнении состояния . Обнаруженные отклонения свойств газа от уравнения (1) учитывали поправками к давлению (Г. Гирн, 1865) и объему (М. Депре, 1864)

p ( V – N ₀ В ) N _А = N ₀ RT .                            (9)

Ван-дер-Ваальс дал поправке к давлению физическое объяснение (1873) и записал уравнение с тремя константами:

( p + А N ₀²/ V ²) ( V – ВN ₀) N _А = N ₀ RT .                      (9)

Константа А является поправкой к давлению, константа В – поправкой к объему. Универсальную газовую постоянную R можно исключить и свести уравнение (9) для газов 1 и 2 при температуре Т и давлении p к многочлену:

p ( V ₂ – V ₁) = p ( N _0,2 В ₂ – N _0,1 В ₁) + ( А ₁ N _0,1²/ V ₁ – А ₂ N _0,2²/ V ₂) +

+ ( А ₂ В ₂ N _0,2³/ V ₂² – А ₁ В ₁ N _0,1³/ V ₁²).                          (10)

22 в ыпуск 2/2019

Уравнения Депре и Гирна также сводятся к аналогичному равенству.

Условие V = V означает, что для суммы (10) введение поправок А и В в уравнение (1) идеального газа не противоречит закону Авогадро, если выполнимы равенства:

А ₁ N _0,1²= А ₂ N _0,2² и N _0,1 В ₁ = N _0,2 В ₂.

Однако значения поправок А и В не обнаружили универсальности: установлено, что А ≠ А и В ≠ В . Тогда возникает неравенство N ≠ N , которое противоречит закону Авогадро. Поэтому происхождение поправок к давлению и объему в уравнении состояния заключается в том, что оно не удовлетворяет закону Авогадро. Поправка, по своей сущности, должна устранить это противоречие.

Противоречие между поправкой в уравнении состояния и законом Авогадро не было разрешено до настоящего времени. В данной работе оно преодолено предположением о том, что частицы могут менять свое качество в зависимости от физического состояния газа при постоянном числе молекул.

В рамках предлагаемой нами модели эта идея реализована следующим образом: поскольку вычисление констант А и В не требует знания состава частиц, уравнение (9) следует записать относительно количества N * единичных и протяженных частиц газа как результата ближнего и дальнего взаимодействия N ₀ исходных (точечных) молекул в форме

( p + АN *²/ V ²) ( V – ВN *) N _А = N * RT . (11)

Тогда требуемое законом Авогадро равенство N0,1 = N0,2 для газов 1 и 2 при температуре Т и давлении p можно свести к выполнению при любых давлениях и температурах двух равенств:

А ₁ N *₁²= А ₂ N *₂² и N *₁ В ₁ = N *₂ В ₂.

В предлагаемой модели они выполнимы для общего количества единичных и протяженных частиц, так как N *₁ ≠ N *₂ в силу химической индивидуальности газов.

Таким образом, математическое описание свойств реальных газов, данное в форме поправок (9) Ван-дер-Ваальса к уравнению (1), не отвечает закону Авогадро, в то время как поправки уравнения (11), наоборот, удовлетворяют этот закон при любом давлении или температуре. Мы видим в этом факте новое содержание теории Ван-дер-Ваальса, которое будет использовано ниже в моделировании газоподобных нанообъектов.

Пример раскрытия величины N* . Уравнения (9) и (11) описывают кубическую pV- кривую с двумя экстремумами. Поскольку N ₀ ≠ N *, их изотермы не совпадают. Сравним их.

Изотерму, на которой экстремумы совмещаются, называют критической, а полученную таким образом точку перегиба – критической точкой с координатами p _с, V _с и T_с . Значения p и T_с определяют непосредственно из опыта и вычисляют константы A = A_m / N _А² и B = B_m / N _А из комбинаций

Am = 27R2 Tс2/ 64pс , Bm = RTс / 8pс критических параметров вещества. Видно, что расчет Am и B не требует знания состава

m

и качества частиц. Тогда критические изотермы уравнений (9) и (11) пересекаются в кри- тической точке, и выражение (4)

β ≡ N ₀ / N *

можно рассматривать как функцию их соответствия.

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 23

Пример раскрытия β как функции давления и температуры . Полагая, что изотермы уравнений (9) и (11) ниже критической температуры также сливаются в экстремальных точках, можно утверждать об их математическом соответствии через величину β. Для N ₀= N _А результат подстановки выражения (4) в (9) можно свести к многочлену

β ³ + а β ² + b β+ c = 0,                                   (12)

константы которого а = –(pBm+ RT)/pV, b = Am/pV 2, c = –AmBm/pV 3

являются комбинациями величин уравнения (9). Очевидно, что уравнение (12) выражает математическое соответствие изотерм уравнений (9) и (11). Таким образом, зависимость величины β от давления и температуры через коэффициенты а , b и c отражает соответствие числа N ₀ исходных молекул газа числу N * его единичных и протяженных частиц.

Пример вычисления величины β . За полтора столетия выполнено большое количество p- , V- , T -измерений газов и жидкостей. Вода является веществом, для которого имеется наиболее полная сводка термодинамических данных [3]. Тщательность этих исследований позволяет решить обратную задачу определения числа единичных и протяженных частиц воды и пара по известным значениям p и V . В таблице представлены рассчитанные по уравнению (12) значения β воды и пара на линии насыщения.

Температурная зависимость отношения β числа исходных молекул N ₀ к числу реальных частиц N * воды и пара по линии насыщения

Температура, К	Значения β, рассчитанные по уравнению (12)
	Пар	Вода
273,16	1,000	1,978
343,15	1,005	2,051
373,15	1,010	2,070
413,15	1,023	2,092
453,15	1,042	2,115
513,15	1,086	2,162
588,15	1,191	2,503
623,15	1,289	2,214
643,15	1,441	1,937
647,15	1,601	1,751
647,27	1,614	1,614

Согласно таблице, значения β можно разделить на две группы по признаку их отличия от единицы. Значение β = 1 трактуется как компенсация сил взаимодействия между молекулами, т.е. газ образован либо единичными, либо точечными частицами. Примером этого случая может служить идеальный газ. Когда β > 1, взаимодействие между молекулами не компенсировано, в веществе формируются протяженные частицы с ограниченным временем жизни. Механизмы их взаимодействия разнообразны и определяются химической индивидуальностью вещества. Вариации β могут быть как монотонными, так и экстремальными. Описание этих случаев для воды и других веществ дано в [6; 8; 16].

24 в ыпуск 2/2019

Геометрический аспект моделирования наносистем в газе

Инерциальное движение молекул может приводить к возникновению наносистемы в газе. Моделирование наносистем из молекул и пустоты строится в нашей модели на положении о равномерном распределении молекул и их энергий в координатном пространстве. Равномерность распределения молекул характеризует константа Авогадро N _А. Равномерность распределения энергий молекул характеризует постоянная Больцмана k . Пропорциональность 1/ k и _А дает основание выделить в координатном пространстве минимальную по размеру и составу ячейку.

Разбиение объема на равные количества ячеек и молекул отвечает условию минимальности размера и состава ячейки. Согласно Авогадро, газ в нормальных условиях содержит 6,0221 · 1023 молекул в объеме 22,41 л. В нашей модели отношение этих чисел равно 37,26 нм3/молекулу. Кубический корень от этого числа равен 3,34 нм. Если его рассматривать как эффективный линейный размер ячейки в координатном пространстве, тогда ограниченную ячейкой пустоту и молекулу можно рассматривать как минимальный нанообъект. Заметим, что минимальная ячейка кристалла не является нанообъектом.

Максимальный объем нанообъекта по условию равен 106 нм3. Поэтому моделирование наносистемы в газе при нормальных условиях не должно превышать 106/37,26 = 26 840 ячеек или молекул. Примечательно, что ~27 000 частиц кристалла также составляют его максимальную наноразмерную подсистему [1]. Это совпадение количеств частиц неслучайно и позволяет авторам быть уверенным в реальном существовании в газе нанообъекта и возможности сравнения газоподобного нанообъекта с кристаллическим.

Метод ячеек случайных форм . Разбиение кристалла на ячейки производят так, чтобы ячейка сохранила симметрию кристалла. Известно 14 способов такого разбиения (О. Браве, 1848). Разбиение газа на ячейки следует осуществить, также отразив реальную симметрию газа. Геометрия газообразного тела случайна. Автор также считает форму каждой ячейки случайной. Выполнение ими пространства можно осуществить бесконечным числом способов. Выделим из них одно из разбиений как мгновенное состояние газа и примем его к рассмотрению как статическую систему ячеек случайных форм. На рисунке 4 случайная форма ячейки имеет минимальную симметрию 1, т.е. может быть совмещена сама с собой только один раз.

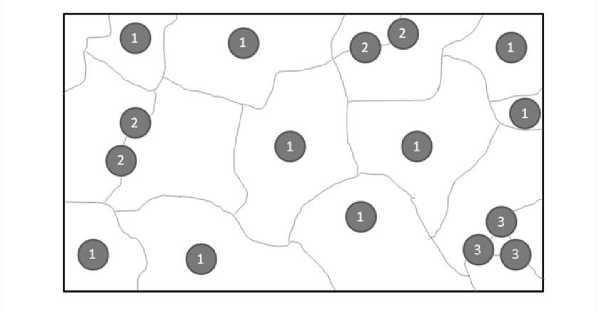
Рис. 4. Статическая схема ячеек случайных форм, поясняющая мгновенные состояния частиц газа

Лаптев В.И. Принципы ab initio в моделировании газоподобных наносистем... 25

На каждую ячейку (см. рис. 4) приходится одна частица: частицы под номером 1 расположены внутри ячеек, 2 – помещены на границе двух ячеек, 3 – занимают узлы трех ячеек. Различие в положении частиц определяет различие их качества.

Заметим, что к рассмотрению недопустима максимальная симметрия ячейки, например симметрия ячейки из атома Дальтона вместе со сферической огранкой теплородом (см. рис. 2). Укладка таких ячеек не выполняет пространство и исключает инерциальное движение частиц в ошибочной модели Дальтона. Однако допустимы к рассмотрению менее симметричные ячейки. Так, выполнение пространства кубическими ячейками (см. рис. 3) привело Дальтона к верному убеждению о существовании внутреннего движения частиц газа и его закону о парциальном давлении в смеси газов. В нашей модели симметрия ячейки минимальна и равна 1.

По условию нашей модели, одна ячейка содержит одну частицу, поэтому для счета частиц в ячейках газа действует известное правило для примитивной ячейки кристалла. Например, если частица находится внутри ячейки, то ее граница остается незанятой. На границе двух ячеек могут находиться только две частицы. Если частица находится в узле, тогда и остальные частицы соседних ячеек располагаются по узлам.

В отличие от кристалла положение частицы в ячейке газа имеет принципиальное значение: в силу инерциального движения молекул газа не только их положение, но и состояние в ячейках переменно. Внутри ячейки молекула является точечной, или условно-сферической, частицей, поэтому столкновения внутри ячейки отсутствуют. На границе ячеек молекула представляет уже единичную частицу. Протяженный объект составят две частицы на границе двух ячеек или три частицы в узлах трех ячеек. Возможны другие комбинации. Именно в граничных состояниях молекул возможно их столкновение.

Ячейка, минимальная по составу и размеру, не способна к самостоятельному существованию вне окружения других ячеек. Только в совокупности с ними она будет наносистемой из одной молекулы и окружающей ее пустоты ячейки. С этой точки зрения протяженная частица является сборкой нескольких наноячеек газа. Поэтому молекулы с сопутствующей ей пустотой как точечные, единичные и протяженные частицы выступают в нашей модели в роли наноразмерного атрибута иерархии газообразного тела, отвечающего за конституцию тела на наноуровне.

Отличие газа от кристалла на наноуровне состоит в том, что в газоподобном теле симметрия наносистемы не связана с ее составом, в то время как связь состава кристалла с его симметрией является предметом кристаллографии и кристаллохимии. Однако в специальных случаях возможно применение к газу решеточной модели.

Заключение

Построение принципов ab initio в моделировании наносистем из молекул и пустоты осуществлено в данной работе при соблюдении нескольких руководящих в методологическом отношении моментов.

• 1.    Отказ от строго точечного описания частиц газа. Представление о частице как о материальной точке, сохраняющей это свойство вне зависимости от свойств окружающей среды и остальных частиц, является лишь приближенным отражением реальности. В излагаемой модели газа лежит новая трактовка понятия частицы, отражающая зависимость протяженности частицы от тех физических условий, в которые эта частица попадает.

• 2.    Новый подход к понятию замкнутости физической системы. Динамика частиц в излагаемой модели описана как сумма инерциального и неинерциального движений. Благодаря этому понятие замкнутости системы приобрело новый смысл, перейдя от классической частицы к понятию о протяженной частице.

• 3.    Подход к моделированию наносистем построен так, что движение является неотъемлемым свойством частиц газа. В излагаемой модели указанная идея осуществляется составлением газообразного тела из частиц и пустоты. Пустота служит источником инерциального движения частиц, которое существует вне зависимости от свойств окружающей среды и физической организации газообразного тела.

26 в ыпуск 2/2019

Принципы ab initio и указанная выше методология их применения позволили автору согласовать уравнения излагаемой модели с законом Авогадро, найти и сформулировать параметры моделирования конституции газа на наноуровне.

Следует подчеркнуть, что излагаемые принципы ab initio в моделировании наносистем не противопоставлены классической теории, но дают возможность уточнить расширение границ ее применимости. Например, указаны границы применимости представления точечной частицы, показано в каких случаях оно теряет смысл и должно быть обобщено до понятия протяженной частицы. Поэтому подход к газу как к системе из частиц и пустоты не ограничивается моделированием газоподобных наносистем.