Принципы ab initio в моделировании наноразмерного объекта как конечного числа узлов кристаллической решетки

В веществе, изделии или иной структуре наноразмерный объект составляет в каждом из трех измерений от 1 до 100 нм. В рамках этого соглашения нанообъект в атомной структуре кристалла может составить от 3 до 30 межатомных расстояний, или от 27 до 27000 атомов, если модуль трансляционного вектора решетки Браве условно принять равным 0,33 нм. Такие группы атомов можно называть кристаллическими нанофрагментами, когда они условно разграничены между собой, или наночастицами, когда они имеют отчетливо выраженную границу с окружающей средой. Объекты с линейным размером менее 1 нм обычно относят к кластерам. В их описании используют квазикристалличе-ское приближение, как пример – используют оси симметрии пятого и седьмого порядков. В дан ной работе нан ообъекты рассмотрены без при-

The principle of simulation of clusters, crystal nanoparticles and nanofragments including a concept about the coordination nanosphere as mathematical description of coordination of the equidistant sites in a crystal lattice or atoms in crystal space are presented. A set of concentric nanospheres covers several tens of clusters or atoms therefore it allows to describе the geometrical and morphological features of clusters, crystal nanoparticles and nanofragments.

ВЕСТНИК 2017

влечения квазикристаллического приближения; вводится понятие о координационной наносфере как математического согласования положений равноудаленных узлов в кристаллической решетке или атомов в кристаллическом пространстве. Набор концентрических наносфер позволил найти новые аспекты в геометрическом и морфологическом описаниях свойств кристаллических кластеров, нанофрагментов и наночастиц из основополагающего принципа – свойств решеток Браве.

История и современное состояние вопроса об уровнях организации кристалла

Конституция кристалла определяется не только энергией взаимодействия, соотношением размеров и поляризацией атомов, но также их числом. Последний фактор важен в идентификации кристаллического объекта или фрагмента для описания иерархии структур кристалла. Такие фрагменты называют структурными единицами и выбирают в этом качестве атом, формульную единицу, ячейку, координационный многогранник, индивид или сам кристалл.

ВЕСТНИК 2017

Каждая из перечисленных выше структурных единиц составляет минимальную часть кристалла, которая характеризует конкретный уровень организации его структуры. Атом и формульная единица отображают химический и стехиометрический составы кристалла; ячейка и координационный многогранник – закономерность атомного расположения; индивид и габитус – организацию кристалла как физического тела.

Длительная дискуссия [1] о структурных единицах кристалла закончилась разграничением понятий о молекуле и формульной единице, ячейке, индивиде (Г.Б. Бокий, С.С. Бацанов, 1954 г.). Молекул в кристалле нет, кроме специального случая молекулярного кристалла, к ячейке которого относят одну формульную единицу. Формульная единица кристалла – условная группа атомов или ионов, состав которой соответствует химической формуле данного вещества.

Ячейкой кристалла называется минимальный воображаемый объем, параллельные переносы которого в трёх измерениях позволяют построить трехмерную кристаллическую решетку в целом. Выбор ее неоднозначен. При моделировании кристаллических структур удобнее использовать ячейку с теми же элементами симметрии, что и конечный объем, так как она воспроизводит не только структуру, но, в конечном счете, и свойства кристалла.

Реальный кристалл состоит из блоков [2]. Эти блоки разориентированы друг относительно друга на 1–3º, реже – до 5º (Г.Б. Бокий, 1985 г.). Отдельный блок кристалла размером 10–7 – 10–8 м считается индивидом. Понятие об индивиде кристалла наиболее полно разработано Г.Б. Бо-кием (1975 г.).

Индивид можно выделить на фотографиях поверхности, полученных с помощью электронного микроскопа в режиме катодолюминесценции [3; 4] (рис. 1).

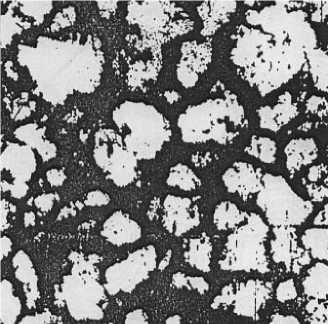
Рис. 1. Катодолюминесцентное изображение полированной поверхности алмаза размером 300 мкм2 (Hanley et al, 1977;

Lang, 1979)

Индивид можно выделить также на оже-электронном изображении [5] (рис. 2).

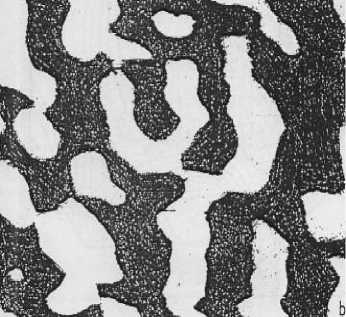
Рис. 2. Оже-электронное изображение поликристаллической пленки сульфида свинца (Petrov, 1992)

Индивид можно выделить также на картах изолиний концентрации ионов по пластинке кристалла, полученных методом оптической спектроскопии [6] (рис. 3)

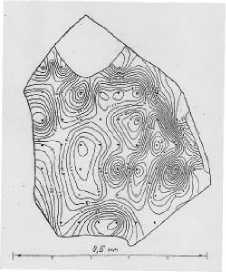
Рис. 3. Карта изолиний концентрации ионов Fe2+ на поверхности пластинки оливина (Bakhtin et al, 1996)

Зародыш кристалла также есть его индивид.

Га́битус – наружный вид кристаллического многогранника, определяемый преобладающим развитием тех или иных граней. Кристаллы одного и того же химического состава могут иметь различный габитус.

Таким образом, в реальном кристалле выделяют четыре подсистемы его организации. Первая отображает химический состав; вторая – расположение атомов; третья – организацию кристалла как физического тела, четвертая – его форму. К минимальным структурным единицам этих подсистем относятся понятия о формульной единице, ячейке, индивиде и габитусе кристаллического многогранника, соответственно.

Кристалл как математическая модель Браве

Модель идеального кристалла строится на идее Браве описывать кристалл как конечной, так и бесконечной геометрическими фигурами: многогранником и решеткой. Многогранник составлен из многоугольников, элементы которых называют в кристаллографии гранью, ребром и вершиной. Решетка представляет собой бесконечную геометрическую фигуру из точек, которые в кристаллографии называются узлами . Действием группы трансляций Браве на точку воспроизводится одноименная решетка. Решетка, возникающая из произвольно выбранной точки кристалла под действием группы трансляций Браве, называется кристаллической . Этот вспомогательный геометрический образ интересен в кристаллографии тем, что относительно каждого узла все остальные расположены одинаково. Для удобства анализа структуры кристалла в узлы такой решетки помещают атом, атомную группу или элемент симметрии. Браве ошибочно помещал в узел молекулу. В общем случае, решетка Браве не совпадает с реальным кристаллом, а узлы не соответствуют атомам. Поэтому в моделях реального кристалла, которые здесь не рассматриваются, следует отличать кристаллическую решетку как математическую модель кристалла и решетку Браве как бесконечную геометрическую фигуру.

Постановка задачи

Кристаллическое пространство в математических моделях бесконечно, реальный кристаллический многогранник обладает конечным объемом. Поэтому возникает задача разбиения пространства на многогранники так, чтобы никакие два многогранника не налегали друг на друга (условие упаковки) и множество этих многогранников заполняло полностью всё пространство (условие покрытия – заполнения). Отыскание возможных способов разбиения кристаллического пространства является одной из задач геометрической кристаллографии.

Метод элементарных ячеек Браве является одним из главнейших, но не единственным способом разбиения бесконечного трехмерного кристаллического пространства на конечные фрагменты: известны разбиения Федорова, Вороного – Дирихле и Делоне. В них фигуры разбиения являются наноразмерными объектами. Здесь мы ставим задачу описать наноразмерные объемы кристаллического пространства, которые больше объема элементарных ячеек Браве, областей Вороного – Дирихле и Делоне.

Математический аспект моделирования кристалла

Выбор и описание фрагмента кристалла как ограниченного объема в безграничном кристаллическом пространстве составляет сущность моделирования наноразмерных кристаллических объектов. Представим этот фрагмент в форме многогранника. Описание его формы дадим через известные фигуры разбиения кристаллического пространства, которые включаются в искомый объем. Поскольку любой сложный кристаллический многогранник можно подвергнуть разбиению на конечное количество простых форм, воспользуемся далее аппаратом простых форм.

Простая форма в геометрии – это совокупность граней, выводящихся друг из друга элементами симметрии точечной группы. Геометрически они различаются по форме, по количеству, по расположению граней относительно друг друга. Всего известно 47 простых форм, их комбинации многочисленны. Идея о простых формах и их комбинациях впервые высказана В. Дависсоном в 1630 году для описания гран-ных форм кристалла.

Грани простой формы эквивалентны в кристаллографическом аспекте, так как совмещаются друг с другом действием операций симметрии данного класса. В комбинациях простых форм грани неэквивалентны и делятся на столько видов, сколько простых форм составляют кристаллический многогранник. Грани реального кристалла в подавляющем числе случаев неэквивалентны в кристаллографическом аспекте. Однако они ориентированы в пространстве так, что отсекают отрезки на трех кристаллографических координатных осях кристалла, которые можно представить как отношение целых чисел. Этот закон открыт Гаюи в 1784 году, носит его имя и составляет основу кристаллографии.

Плоская сетка из атомов видится нам как грань кристалла. Идея свернуть грань кристалла в точку составляет вклад Браве в кристаллохимию. Система таких точек должна быть аналогом простой формы в том смысле, что грани кристалла располагаются по закону простых форм, но атомы – по законам систем таких точек. Совокупность симметрично эквивалентных точек (позиций), связанных между собой симметричными преобразованиями пространственной группы, называется в кристаллографии правильной системой точек. Известно более тысячи правильных систем точек, их комбинации многочисленны. Правильные системы точек описаны Е.С. Федоровым в 1885 году.

ВЕСТНИК 2017

ВЕСТНИК 2017

Простая форма и правильная система точек: химический аспект

Правильную систему точек можно получить из одной точки, повторив ее всеми операциями симметрии, свойственной данной пространственной группе. Справедливо обратное утверждение. Поэтому правильная система точек составляет геометрический образ закона пространственного расположения атомов в кристалле, в котором атомы разного сорта не могут занимать одну систему.

Основной закон химии имеет название «закон кратных отношений», который в математическом аспекте соответствует утверждению, что атомы соединяются по закону отношений целых чисел. Реальный кристалл – химическое соединение, и его гранная форма подчиняется закону Гаюи, который также называют законом целых чисел , или законом рациональности . Названия, различные по форме, но одинаковые по математической сущности, сложились не случайно. Их сущность означает, что расположение атомов в кристаллическом пространстве и формы кристаллических многогранников обусловлены химическим составом вещества. Однако эта связность неоднозначна. Например, кристаллы одинакового химического состава могут иметь различную гранную форму, простой и сложный кристаллический многогранник. В то же время, кристаллы одинаковой формы могут иметь разный химический состав (явление изоморфизма). Любой из таких кристаллических многогранников можно подвергнуть разбиению на конечное количество простых форм. Поэтому грани кристалла, равные в кристаллографическом аспекте, имеют одинаковый химический состав с тем отличием от правильной системы точек, что и грани кристалла могут составить атомы разных сортов. Грани кристалла, разные в кристаллографическом аспекте, различаются по химическому составу и могут отличаться от стехиометрического состава вещества.

Атомно-координационный аспект моделирования кристалла

Пусть кристалл для простоты описания образован атомами одного сорта. Определяя число ближайших равноудаленных атомов, выделяют многогранник. Его образуют прямые линии, соединяющие центры ближайших равноудаленных атомов. Такой многогранник называют координационным, его используют в наглядной иллюстрации ближайшего окружения атома. Однако геометрия координационного многогранника не согласуется с микросимметрией кристалла. В данной работе координация атомов представле- на как математическое согласование их положений в кристаллическом пространстве.

Идея выделения в кристалле координационного многогранника в формах октаэдра и тетраэдра принадлежит Л. Полингу (1929) [7]. Более сложные и менее симметричные формы координационных многогранников предложил Н.В. Белов (1947) [8]. Координация атомов в кристалле была рассмотрена Урусовым В.С. 1987) и Грековым (1995), О’Keeffe (1991) и Раrthe (1990). Упаковка координационных многогранников просто и наглядно иллюстрирует структуру кристалла как совокупность некристаллических нанораз-мерных объектов.

Поместив атом в систему координат, можно выделить вокруг него набор концентрических сфер, объединяющих равноудаленные атомы. Поскольку в эти сферы вписаны координационные многогранники, назовем сферы координационными. Число этих сфер бесконечно. Радиусы ближайших к центральному атому сфер отвечают наноразмерному масштабу. Подчеркивая это свойство сфер, назовем их координационными наносферами.

Координационные наносферы иллюстрируют структуру кристалла не как некристаллические наноразмерные объекты, а как упаковка кристаллических наноразмерных фрагментов с теми же элементами симметрии, что и бесконечное кристаллическое пространство. Математическое моделирование кристаллических наноструктур удобнее вести по этому пути, так как он воспроизводит не только наноструктуру, но, в конечном счете, и свойства кристалла как микро-и макроструктуры.

В кристаллохимии отсутствует геометрическая интерпретация закона целых чисел для гранных форм, выделенных как в правильной системе точек, так и в кристаллической решетке для координационных сфер и многогранников. Поэтому в данной работе представлен геометрический аспект задачи моделирования кристаллических наноразмерных объектов, который состоит в отыскании математического выражения между симметрийными свойствами простых форм, координационных многогранников и правильных систем точек в единстве с химическим составом кристаллического вещества.

Математическое обоснование координационного многогранника

Узел решетки, или правильной системы, не размножается элементами симметрии, входящих в комплекс элементов симметрии данного узла и эквивалентной позиции правильной системы. В работе развивается идея о том, что плоскость вне этой позиции будет размножена и образует одну из правильных форм в зависимости от ее положения относительно элементов симметрии. Возможны два варианта положения вершин простой формы относительно начальной плоскости и начальной позиции. В первом варианте все вершины или часть их принадлежат эквивалентным в кристаллографическом аспекте позициям относительно выбранной позиции. В другом варианте все вершины или часть вершин принадлежат неэквивалентным в кристаллографическом аспекте позициям относительно выбранной позиции.

Поместим атом в узел решетки, назовем его исходным. Расположим возле атома пробную грань так, чтобы реализовался один из двух способов расположения вершин образованной элементами симметрии простой формы. Тогда линии между вершинными атомами образуют координационный многогранник. В обоих вариантах симметрия простой формы должна быть закономерным образом связана с симметрией координационного многогранника, в центре которого находится исходный атом. Поэтому координационный многогранник в данной работе представлен простой формой или комбинацией нескольких простых форм.

В координационном многограннике воспроизводится не только структура, но и химический состав кристалла. Нами составлено равенство между числом Z формульных единиц и числом q дополнительных трансляций в элементарной ячейке Браве, числом s граней координационно- го многогранника, стехиометрическим коэффициентом pi химического элемента в химической формуле кристаллического вещества в виде [9]:

Z = ( q + 1) s ( p_i ) ^–1Σ _n (1 ⁄ S_i ) / Σ _m (1 ⁄ S_i *), (1) где n – число правильных систем точек в кристаллической структуре. S_i – величина симметрии правильной системы точек, численно равная отношению порядка пространственной группы симметрии к кратности правильной системы точек. Символ S_i * обозначает величину симметрии грани простой формы, которая равна отношению порядка точечной группы симметрии к числу граней простой формы. Величина m соответствует числу простых форм, комбинация которых образует координационный многогранник.

Отсутствие в уравнении (1) полного набора трансляций Браве (присутствуют только дополнительные трансляции) позволяет разделить координационные многогранники на две группы по следующему признаку. Вершины одних координационных многогранников могут быть совмещены с выбранным началом кристаллографических координат элементами симметрии без участия трансляции. Вершины других координационных многогранников требуют для этого трансляционных переносов. В табл. 1 на примере кубических решеток Браве первые координационные многогранники помечены в первой колонке символом «•».

Таблица 1

ВЕСТНИК 2017

Координационные многогранники и сферы кубических решеток Браве

	Координационный многогранник	Координаты вершины	Число вершин	Число граней	Радиус координационной сферы
cP – примитивная решетка
•	октаэдр	0,0,1	6	8	1
•	кубооктаэдр	0,1,1	12	14	1,414
•	куб	1,1,1	8	6	1,732
	октаэдр	0,0,2	6	8	2
	кубооктаэдр	0,1,2	24	14	2,236
	кубооктаэдр + ромбододекаэдр	1,1,2	24	26	2,450
cI – объемоцентрированная решетка
•	куб	1/2,1/2,1/2	8	6	0,866
•	октаэдр	0,0,1	6	8	1
•	кубооктаэдр	0,1,1	12	14	1,414
	кубооктаэдр + ромбододекаэдр	1/2,1/2,3/2	24	26	1,658

ВЕСТНИК 2017

•	куб	1,1,1	8	6	1,732
	октаэдр	0,0,2	6	8	2
cF – гранецентрированная решетка
•	кубооктаэдр	0,1/2,1/2	12	14	0,707
•	октаэдр	0,0,1	6	8	1
•	кубооктаэдр + ромбододекаэдр	1/2,1/2,1	24	26	1,225
•	кубооктаэдр	0,1,1	12	14	1,414
	кубооктаэдр	0,1/2,3/2	24	14	1,581
•	куб	1,1,1	8	6	1,732
	кубооктаэдр + ромбододекаэдр	1/2,1,3/2	24	26	1,937
	октаэдр	0,0,2	6	8	2

Уравнение (1) выполняется для всех координационных многогранников в атомной структуре кристалла; оно является математическим обоснованием выделения координационного многогранника.

Математическая связность симметрии конечного и бесконечного объектов

Классификация атомов по признаку трансляционных переносов имеет принципиальное значение для геометрического и морфологического описаний кристаллических наноразмер-ных объектов. Так, решетка Браве ( n = 1) может быть рассмотрена как правильная система точек с максимальной симметрией S ее позиций. Тогда число формульных единиц в ячейке Браве равно кратности k правильной системы точек, p_i = 1, S = S ₀ / k , где S ₀ – порядок пространственной группы симметрии решетки Браве. Подставляя это соотношение в (1), получим [10]

S ₀ / ( q + 1) = s / Σ_m (1 / S *). (2)

Левая часть равенства включает символы свойств бесконечной фигуры – правильной системы точек, бесконечного числа узлов решетки Браве. Его правая часть включает символы свойств конечной фигуры – простой формы или координационного многогранника данного узла решетки Браве. Такой узел может быть выбран произвольно. Поэтому равенство (2) представляет собой математическое выражение единства ближнего и дальнего порядков решетки Браве, математической связности конечного и бесконечного объектов, конечного объема и бесконечного кристаллического пространства.

Моделирование кристаллического нанофрагмента по числу координационных наносфер

В решетке можно выделить бесконечное множество координационных многогранников, которые можно разделить на два вида по признаку их принадлежности к ближнему или дальнему порядкам. В табл. 1 координационные многогранники ближнего порядка решеток Браве помечены в первой колонке символом «•»; остальные составляют дальний порядок. Видно, что атомы ближнего порядка располагаются в сфере радиусом не бóльшим, чем 1,732 модуля единичного трансляционного вектора решетки Браве. Он удовлетворяет линейному критерию нанообъекта, поэтому ближний порядок кристаллической решетки можно характеризовать набором из координационных наносфер.

Узлы ближнего порядка решетки распределяются по нескольким наносферам. В трех кубических решетках можно выделить 3, 4 и 5 наносфер, количество которых достигает максимального числа в триклинной и ромбической гранецентрированной решетках (13 наносфер, табл. 2).

Вариация числа наносфер позволяет характеризовать протяженность ближнего порядка кристалла количеством координационных наносфер. Наибольшая наносфера ближнего порядка имеет радиус, равный большой диагонали ячейки Браве. Тогда количество координационных наносфер равно числу всех возможных расстояний между узлами в ячейке Браве. В 14 ячейках Браве можно насчитать 108 координационных наносфер ближнего порядка [11].

Координационные наносферы ближнего порядка решетки Браве

Симметрия решетки	Символ решетки	Число дополнительных трансляций, q	Число трансляций в ячейке	Максимальное число координационных наносфер в ближнем порядке, nб
P – примитивные решетки
Триклинная	aP	0	13	13
Моноклинная	mP	0	11	9
Ромбическая	oP	0	11	7
Тетрагональная	tP	0	6	5
Гексагональная	hP	0	11	5
Кубическая	cP	0	3	3
I – объемоцентрированные решетки
Ромбическая	oI	1	11	8
Тетрагональная	tI	1	6	6
Кубическая	cI	1	3	4
C – б азоцентрированные решетки
Моноклинная	mC	1	15	12
Ромбическая	oC	1	13	9
R – дважды объемоцентрированные решетки
Гексагональная	hR	2	19	9
F – гранецентрированные решетки
Ромбическая	oF	3	20	13
Кубическая	cF	3	4	5
			Всего 146	Всего 108

ВЕСТНИК 2017

Моделирование координационной наносферы по числу узлов

Характеризуя кристаллическую решетку набором из n концентрических наносфер, можно найти число входящих в них узлов по формуле

N = 1 + Σ _n N_n , (3)

где N_n – число узлов, приходящихся на одну из n наносфер. Они находятся геометрическим построением как число вершин координационного многогранника. Для каждого типа решетки, набора ее элементов симметрии существует предельное количество n_б наносфер ближнего порядка, которое приведено в табл. 2 для всех типов решеток. Рассчитанное по формуле (3) предельное число узлов N _{б пред} в наносферах ближнего порядка всех типов решеток Браве приведено в табл. 3.

Связность симметрии решетки и предельного числа узлов наносфер

Из сопоставления найденных значений N _{б пред} с числом узлов ячейки решетки Браве определим, что увеличение предела количества узлов в ближнем порядке от 27 до 63 коррелирует с повышением симметрии кристаллического пространства. Вариация ближнего порядка по предельному числу N _{б пред} узлов решетки свидетельствует об обоснованности выделения в кристалле координационных наносфер как альтернативного развития метода координационных многогранников для наглядного изображения особых свойств кристаллических наноструктур.

Геометрический аспект выделения в кристалле координационных наносфер следует из анализа табл. 2, 3: вариация величины N _{б пред} определяется симметрией кристаллической решетки так, что предельное число узлов N _б,пред корре-

Вариация числа атомарных конфигураций в ближнем порядке решетки Браве

ВЕСТНИК 2017

Симметрия и символ решетки		Максимальное число координационных наносфер в ближнем порядке, nб	Максимальное число узлов в ближнем порядке, N б,макс	Число возможных конфигураций из N узлов, Ψ
P – примитивные решетки
Триклинная	aP	13	27	27
Моноклинная	mP	9	27	27
Ромбическая	oP	7	27	27
Тетрагональная	tP	5	27	27
Гексагональная	hP	5	27	27
Кубическая	cP	3	27	27
I – объемоцентрированные решетки
Ромбическая	oI	8	35	595
Тетрагональная	tI	6	35	595
Кубическая	cI	4	35	595
C – б азоцентрированные решетки
Моноклинная	mC	12	39	741
Ромбическая	oC	9	39	741
R – дважды объемоцентрированные решетки
Гексагональная	hR	9	43	12341
F – гранецентрированные решетки
Ромбическая	oF	13	63	595665
Кубическая	cF	5	63	595665
		Всего 108

лирует с числом координационных наносфер и числом дополнительных трансляций q на общем фоне комплекса элементов симметрии. Решетки с равным числом q дополнительных трансляций в элементарной ячейке Браве имеют одинаковый предел числа N _б,пред узлов в наносферах ближнего порядка решетки. В ряду решеток Браве минимальное значение N _{б пред} имеет примитивная решетка с максимальным числом наносфер, максимальное N _{б пред} имеет гранецентрированная решетка с максимальным числом дополнительных трансляций. Таким образом, увеличение количества координационных наносфер в ближнем порядке кристаллического фрагмента свидетельствует о понижении его симметрии.

Моделирование кристаллических нанофрагментов по числу узлов по формулам (2), (3) состоит в изучении корреляции предельного числа узлов в ближнем порядке кристалла с числом координационных наносфер и числом дополнительных трансляций в ячейке.

Наносфера как источник математического обоснования запрета на комбинацию из решеток

Комбинации из простых форм или правильных систем точек используются для описания макро- и микросимметрии кристалла. При этом подчеркивается, что решетка Браве или кристаллическая решетка не может быть представлена комбинацией решеток. Понятие о координационной наносфере позволяет найти этому правилу математическое обоснование.

Поместим атомы в узлы решетки Браве и выделим один из них как начальный объект моделирования и счета координационных наносфер. Совмещение центра наносферы с атомом не- однозначно, но выбор другого атома или точки межузельного пространства в качестве центра сферы не изменит распределения атомов по наносферам, оно вновь воспроизведется. В этом заключается физический аспект единства ближнего и дальнего порядков кристалла. Поэтому моделирование координационной наносферы по числу атомов не требует ее фиксации к атомам ближнего и дальнего порядка кристалла, элементам симметрии или узла решетки в бесконечном кристаллическом пространстве.

Пусть координационная наносфера начального атома охватывает N других атомов. В моделировании атомарных нанофрагментов представляет интерес число Ψ возможных пространственных комбинаций из Z атомов при условии Z ≤ N . Согласно формулам комбинаторики, это число равно

Ψ = N !/( N – Z )! Z !. (4)

Область значений Ψ ограничена условием Z ≤ N . Действительно, когда Z = N , возможна одна пространственная атомарная конфигурация, так как Ψ = 1, т.е. кристаллическая решетка или решетка Браве не может быть представлена комбинацией решеток. В моделировании атомарных нанофрагментов представляют интерес другие комбинации N и Z из формулы (4).

Распределение атомов по координационным наносферам

В бесконечном кристаллическом пространстве величины N и Z независимы в области их значений. Напротив, в кристаллографии ближнего порядка величины N и Z взаимосвязаны. Так, значения N включают в себя предельные числа 27, 35, 39, 43 и 63 атомов, которые определяются набором элементов симметрии кристаллического пространства (табл. 2, 3). Величина Z не может быть больше N , поэтому она также имеет предельное значение 63.

Таким образом, в моделировании атомарных кристаллических нанофрагментов представляет интерес число Ψ возможных пространственных комбинаций из 1 ≤ Z ≤ 63 атомов ближнего порядка. В кристаллохимии величина Z имеет смысл числа формульных единиц. Для ячейки Браве с q дополнительных трансляций выполняется равенство Z = q + 1. Пространственные комбинации из 1 ≤ Z ≤ 4 атомов представляют важнейший объект моделирования кристаллических нанофрагментов.

Так, для Z = 1 возможно максимальное значение N , равное 2727 (табл. 2, 3). Для Z = 2 возможны значения N , равные 35 и 39. Для Z = 3

возможно максимальное значение N , равное 43, а для Z = 4 значение N составит 63. Когда Z = 1 и N = 27, возможны вариации 27 конфигураций из атомов ближнего порядка, так как и Ψ = 27. Значения N и Ψ для решеток Браве всех типов приведены в табл. 3.

Согласно (4), для Z = 2 атомы могут составить Ψ = 39!/(39 – 2)!2! = 741 вариантов конфигураций нанофрагментов в базоцентрированной решетке. Ячейку решетки с Z = 2 можно выбрать произвольным способом. Это означает, что атомы можно расположить в ближнем порядке 741 способом в 12 координационных наносферах для моноклинных и в 9 наносферах – для ромбических кристаллов. Конфигурации нанофрагментов будут различны по симметрии, но ячейка Браве имеет наибольшую симметрию, чем другие конфигурации атомов нанофрагмента.

Моделирование нанофрагментов по числу атомов состоит в изучении корреляции предельного числа узлов в ближнем и дальнем порядках кристалла с числом координационных наносфер, числом дополнительных трансляций в ячейке по формулам (1) – (4).

Морфология наноразмерных объектов из атомов

В минералогии морфология отражает всю историю образования и последующего изменения кристалла. Симметрия кристаллов получает наружное выражение только тогда, когда они имеют возможность свободно расти без каких-либо помех. Форма кристалла зависит от многих факторов, один из которых – форма элементарной ячейки.

В кристаллохимии морфология нанофрагмента должна отражать всю историю его образования и последующего изменения пространственного расположения небольшого числа атомов. Нанофрагмент может составить от 3 до 30 межатомных расстояний. Целью данной работы является рассмотрение изменчивости кристалломорфологии таких нанофрагментов, т.е. описание кристаллографических разновидностей наноразмерных объектов из атомов без учета их химического состава.

В основу кристалломорфологии нанофрагментов можно положить тот факт, что не все трансляции ячеек Браве с равным модулем располагаются по отношению к кристаллографическим осям таким образом, что могут быть совмещены друг с другом осью симметрии. Причиной является отличие их углов с кристаллографическими осями от угловых параметров ячейки. Такие трансляции можно считать неравноценными в кристаллографическом аспекте. Напри-

ВЕСТНИК 2017

Перечень трансляционных векторов в ячейке Браве

ВЕСТНИК 2017

Символ решетки	Число трансляций в ячейке	Координаты трансляций. Координаты начала трансляций 0,0,0 опущены.	Максимальное число координационных сфер в ближнем порядке, n
aP	13	a 00*, 0 b 0, 00 c , ab 0, a 0 c , 0 bc , abc , ( a 00-0 b 0), ( a 00-0 bc ), ( a 00-00 c ), (00 c - ab 0), (00 c -0 b 0, (0 b 0- a 0 c )	13
mP	11	a 00, 0 b 0, 00 c , ab 0, a 0 c , 0 bc , abc , ( a 00-0 b 0), ( a 00-00 c ), ( a 00-0 bc ), (0 b 0-00 c )	9
oP	11	a 00, 0 b 0, 00 c , ab 0, a 0 c , 0 bc , abc , ( a 00-0 b 0), ( a 00-00 c ), ( a 00-0 bc ), (0 b 0-00 c )	7
tP	6	a 00, 00 c , aa 0, a 0 c , abc , ( a 00-00 c )	5
hP	11	a 00, 0 a 0, 00 c , aa 0, a 0 c , 0 ac , aac , ( a 00-0 a 0), ( a 00-00 c ), ( a 00-0 ac ), (0 a 0-00 c )	5
cP	3	a 00, aa 0, aaa	3
oI	11	a 00, 0 b 0, 00 c , ab 0, a 0 c , 0 bc , ( a /2, b /2, c /2), ( a 00-0 b 0), ( a 00- a /2, b /2, c /2), ( a 00-00 c ), (0 b 0-00 c )	8
tI	6	a 00, 00 c , aa 0, a 0 c , ( a /2, b /2, c /2), ( a 00-00 c )	6
cI	3	a 00, aa 0, ( a /2, a /2, a /2)	4
mC	15	a 00, 0 b 0, 00 c , ab 0, a 0 c , 0 bc , abc , ( a /2, b /2, c ), ( a 00-0 b 0), (0 b 0-00 c ), (00 c - a 00), ( a 00-0 bc ), ( a 00- a /2, b /2, c ), ( ab 0, a /2, b /2, c ), (0 b 0- a /2, b /2, c )	12
oC	13	a 00, 0 b 0, 00 c , a 0 c , 0 bc , abc , ( a /2, b /2, 0), ( a /2, b /2, c ), ( a 00- a /2, b /2, 0), ( a 00-00 c ), ( a 00-0 bc ), ( a 00- a /2, b /2, c ), (0 b 0-00 c )	9
hR	19	a 00, 0 a 0, 00 c , aa 0, a 0 c , 0 ac , aac , ( a /3, 2 b /3, 2 c /3), ( a 00-0 a 0), (0 a 0-00 c ), (00 c - a 00), ( aa 0-00 c ), (0 a 0- a 0 c ), ( a /3, 2 a /3, 2 c /3-00 c ), ( a /3, 2 a /3, 2 c /3-0 ac ), ( a/ 3, 2 a /3, 2 c /3- aac ), ( a /3, 2 a /3, 2 c /3- a 0 c ), ( a /3, 2 a /3, 2 c /3- aa 0), ( a /3, 2 a /3, 2 c /3-0 a 0)	9
oF	20	a 00, 0 b 0, 00 c , ab 0, a 0 c , 0 bc , abc , ( a /2, b /2, c ), ( a , b /2, c /2), ( a 00-0 b 0), ( a 00-00 c ), ( a 00-0 bc ), (0 b 0-00 c ), ( a /2, b /2, c -0 b 0), ( a /2, 0, c /2- a , b , 0), ( a /2, 0, c /2- a , b , c ), ( a , b /2, c /2-00 c ), ( a /2, b /2, 0- a /2, 0, c /2), ( a /2, b /2, 0- a , b /2, c /2), ( a /2, b /2, c /2- a , b /2, c /2)	13
cF	4	a 00, aaa , ( a , a /2, 0), ( a , a /2, a /2)	5
	Всего 146		Всего 108

мер, к ячейке кубической решетки относятся 7 трансляций, которые могут быть сведены к трем трансляциям (000-а00), (000-аа0) и (000-ааа). Наибольшим числом неравнозначных кристал

лографических направлений - двадцатью - обладает ромбическая гранецентрированная ячейка (табл. 2). Перечень всех таких трансляций дан в табл. 4. В 14 типах ячеек Браве их оказалось 146.

Можно получить 146 многогранников, расположив плоскость и операции симметрии перпендикулярно каждой трансляции из табл. 4. С другой стороны, известны 146 кристаллографических разновидностей 47 простых форм (Г.Б. Бокий, 1939 г.). Совпадение этих чисел нельзя считать случайностью, поскольку симметрия позиций правильной системы точек и граней простой формы описывается одинаковыми классами и математически выражается уравнением (2).

Критерий роста в концепции координационных наносфер

Поместив в узлах решетки атомы, определим предмет моделирования кристаллических нанофрагментов по числу атомов как изучение пространственных конфигураций из предельного и меньшего числа атомов в ближнем порядке кристалла по всем координационным наносферам.

Материальное наполнение координационной наносферы с предельным N _{б пред} и меньшим количеством атомов в ближнем порядке не требует трансляционных движений. Наносистема атомов, лишенная трансляций, не обладает способностью материального роста вне кристаллического пространства, ее нельзя назвать кристаллическим наноиндивидом или зародышем кристалла. Атомам в большем количестве, чем N _{б пред}, присуще трансляционное движение. Они могут составить кристаллический наноиндивид, так как такая атомная система приобретает способность к росту числа атомов.

Координационные сферы ближнего порядка описывают одну и более ячеек Браве. Поэтому другим аспектом моделирования наноразмер-ных объектов из атомов является изучение числа Ψ возможных комбинаций как вариации числа Z _i формульных единиц в ряду из n координационных сфер в ближнем порядке кристаллического пространства.

Атомы ближнего и дальнего порядков в кристаллическом пространстве не составляют физической поверхности или грани: начало кристаллографических координат можно совместить с любой позицией правильной системы точек, решетки Браве или кристаллической решетки. Поэтому в кристалле нельзя выделить наночастицу, и кристалл не может быть рассмотрен как сумма частиц из атомов ближнего порядка или как сумма наноразмерных частиц. Другими словами, кристаллический нанофрагмент отличается от нанокристаллического индивида тем, что у нанофрагмента отсутствует способность к росту, увеличения размера и массы. Если нанофрагмент по какой-либо причине приобретает гранную форму, то его можно назвать наночастицей. Поэтому критерий моделирования из атомов наноразмерных частиц и кристаллических наноиндивидов имеет противоположную направленность: либо абсолютное подавление роста наноразмерного объекта вещества, либо их всемерная активизация.