Принципы моделирования многофазного течения в системах сетевой гидравлики и продуктивных пластов

Актуальность точных и достоверных расчетов многофазных систем, как в области сетевых задач гидродинамики, так и в условиях продуктивных пластов неоспорима [1–9]. Для систем поддержания пластового давления это критически важно, так как внутри продуктивных пластов происходит активный энергообмен между водой и нефтью.

Существует до сих пор не решенная проблема выделения критерия (ев) структурной неоднородности потоков, состоящих из нескольких разнородных компонентов. В различных гидродинамических условиях [12, 13] компоненты формируют так называемые элементы течения (потока): струи, глобулы, капли сферической и вытянутой формы, слои и т.п.

Особо сложной задачей является однозначный выбор факторов зарождения и преобразования структуры потока и всех его элементов.

В данной работе авторы сделали попытку создать систему факторов, которые позволяют сквозным образом описать структуру потока через элементы потока каждого компонента и функций их взаимодействий.

Предполагается, что поток может состоять из m компонентов любой природы и агрегатного текучего состояния. Течение в первом приближение осуществляет в неком контрольном неделимом объеме.

Итак, введем первый фактор, влияющий на взаимодействие фаз, это фактор раздробленности компонента i в контрольном объеме V ai =

V i^e V ^,

где V ^e – объем элемента в объеме компонента – i , м³.

Этот фактор показывает долю объема элемента в общем объеме.

Элементами потока могут быть капли, глобулы, струи, полосы, кольцевые структуры (рис. 1).

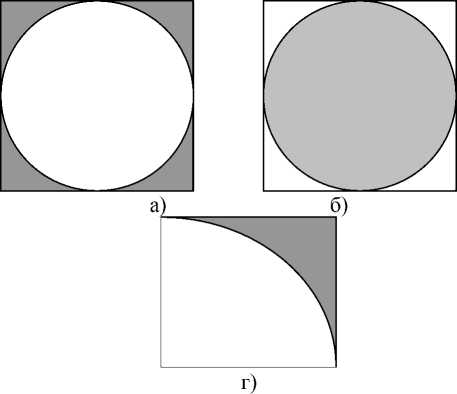
Рис. 1. Элемент потока в сечении контрольного объема: а – сфера; б – область окутывающая сферу; г – выбор элемента позволяет учесть инверсию эмульсии.

Чем меньше объем (не обязательно размеры) элементов компонента в потоке, тем меньше фактор ^a i .

Когда a i =1, тогда объем, например, капли или глобулы полностью покрывает контрольный объем (КО), т.е. форма капли совпадает с формой контрольного объема. При этом насыщенность компонента - О^ будет равна 1. Примером такого случая может служить кольцевая и расслоенная структура (рис. 2).

Как видно из рис. 2 одноэлементные структуры потока не отличаются по фактору раздробленности, что вполне логично. Расположение элементов потока относительно других компонентов, безусловно, будет влиять на фактор α. Для КО кубической формы ограниченными с какой-либо грани твердым телом, с целью учета положения слоев относитель- но граней объема потребуется коэффициент связи компонента с гранями.

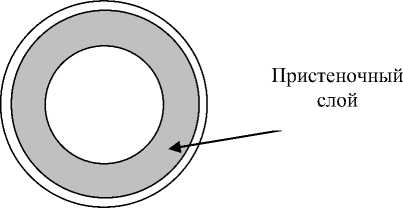
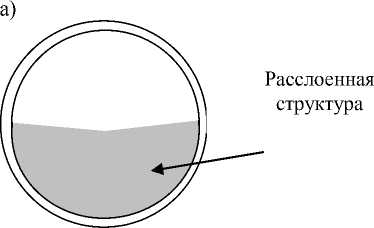
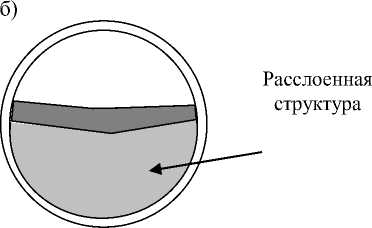
Рис. 2. Примеры структур с одним элементом потока: a =1, ^ е [0,1] .

Количество элементов i -го компонента в контрольном объеме будет

V ct    V ct   ст

V = Va => n =— =--= —.

i      i   v e    Va  a

Т.е. когда объем элемента равен всему объему среды, то элемент один. Равно, как если a = ст, то элемент тоже один.

Введем критерий/фактор, показывающий рациональность формы элементов компонента (пузырьков, струй, лент и т.п.) .

Этот фактор отражает форму элемента и показывает отношение боковой площади элемента, т.е. площади поверхности внешнего контакта (границы) к площади контрольного объема

Sie

Pt    ^ , д.е., где S e – средняя боковая поверхность кап-ли/глобулы i-го компонента, м2.

S – боковая поверхность контрольного объема, м².

Почему выбрана площадь поверхности элемента. Дело в том, что если вместо нее брать периметр в поперечном сечении, то для сферических капель и квазицилиндрических струй, четок и снарядных структур этот параметр будет одинаковым.

Для нормирования выбрана площадь контрольного объема, вследствие того, что она неизменна и всегда (за исключением кольцевой структуры) будет больше боковой площади одного элемента потока - капели, глобулы, струи и полосы. Так неравномерность распределения вдоль потока компонента также учитывается в данном факторе - в .

Направление, по которому происходит вытягивание струй и т.п. можно считать известным из текущего вектора скорости движения.

Проведем проверку классических структур для оценки инвариантности относительно введенных факторов.

Вариант 1. Полного заполнение цилиндрического или любого другого КО дает нам а = 1.0, в = 1.0, ст = 1.

Когда элементом потока является струя квази-цилиндрической формы, то факторы будут:

nr2 L   r2 п  1nrLr а = —=  , в == — nR2 L  R2     1nRLR

•

Вариант 2. Сферические капли в цилиндрическом КО.

4 r3

а =--z—, в = 2,

3 R2L где r - радиус сферы; R - радиус контрольного объема; L - длина контрольного объема.

Для удобства анализа введем пси-фактор, показывающий степень раздробленности потока компонента и совершенство форм элементов

а

I/. =

Pi

Пси-фактор здесь

₂ r ²

RL

„ = а= = vr?l = 2 _L в

ст

Количество элементов потока n = — а r2    3 R

RL

3 R ² L ct

4 r ³

•

Если радиус сферы равен радиусу КО, тогда

4R     R а =    , в = 2 —,

3L      L

Пси-фактор

4R ал 2,1

v = в=^ = 3

L

4 R

Насыщенность ст =    , для длины канала

3L равной 2R будет - ст = —.

Если сфера по малому диаметру равна диаметру канала, при этом вытянута вдоль канала (аналог снарядной структуры), то пси-фактор будет увели- чиваться.

Определение количества элементов связано с допущением, что количество капель по длине канала и по площади сечения примерно равны.

Таким образом, получается, что при радиусе капли равном радиусу канала пси-фактор равен 2/3. При уменьшении радиуса пси-фактор падает, что отражает более сильное взаимодействие компонентов через трение.

Получим функцию от 0 до 2/3, когда сфера перекрывает весь КО в сечении, но не весь в объеме (рис. 3).

В процессе вычисления сил трения потребуется вычислить суммарную площадь соприкосновения фаз. Для начала нужно вычислить суммарную поверхность всех элементов потока через известные на данный момент значения а и в • в -фактор позволяет вычислить среднюю площадь элемента Se = ^S, а а -фактор количе ство элементов n =

CTi а-

Для включения в расчет нам понадобится натуральное выражение площади соприкосновения фаз. Для канала, в котором, как по площади, так и по длине равномерно распределены текучие среды. Таким образом можно получить суммарную поверхность всех элементов компонента i z se=nAs=ст- ^S.

* а

При этом в качестве настроечных функций можно ввести вероятность взаимодействия компонента i с компонентом j в виде - g_t j ( ст^, стj ) •

На рис. 3 показана зависимость пси-фактора от радиуса капель. По-мере роста размеров капель пси-фактор реагирует линейным ростом.

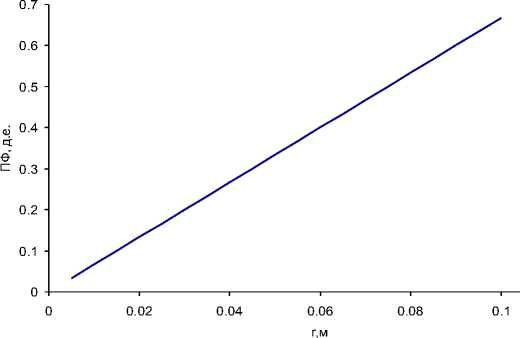
Рис. 3. Зависимость пси-фактора для сферических капель в цилиндрическом канале от их размера.

пузырьковая

струйная

Рис. 4. Переход от пузырьковой структуры к струйной.

Логично полагать, что при деформации капель в сторону вытягивания вдоль канала, т.е. форма будет стремиться к цилиндру (или эллипсоиду) и отношение их объемов к боковым поверхностям будет расти, стремясь к единице.

Рассмотрим случай струйного течения. Для нашего случая ( r - радиус струек, R - радиус цилиндрического канала)

V,e S  nr2L 2nRLr

^, === i S" V  2nrL nR2LR

Логично предположить, что при переходе от пузырьковой структуры к струйкам (промежуточные моменты - вытягивание капель вдоль канала, локальная четочная структура, а затем струйки), см. рис. 4.

Как видно из рис. 5 пузырьковый режим переходит к струйному, и далее достигнет предела r=R ( R =0,1 м в примере).

Наиболее неоптимальный с позиции минимума энергии (минимальная производная пси-фактора по размеру - r ) будет лентовидная или кольцевая структура при малых толщинах ( r ), когда каждый элемент компонента i будет иметь минимальный объем при больших боковых площадях.

Вышеописанные теоретические аспекты не ограничивают применения предложенного фактора, т.к. линейные участок (рис. 4, 5) характеризуют идеальные формы. Для вычленения характерных размеров элементов структуры можно опираться на размер канала и его боковую поверхность.

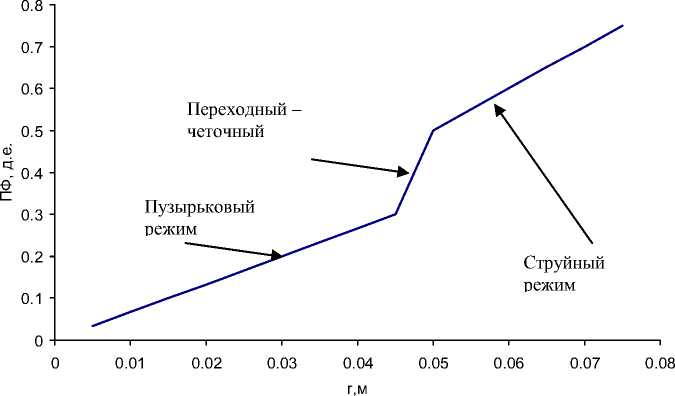
Рис. 5. Пси-фактор от радиуса пузырьков, четок и струй.

Так теоретическую зависимость

Y i ^{( r} ) лучше

построить в относительных координатах

(рис. 6).

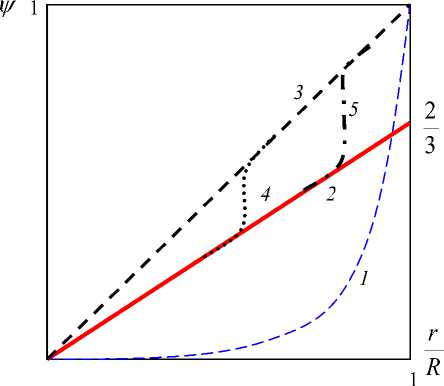
Рис. 6. Сводный график теоретической зависимости пси-фактора от характерного размера элементов структуры расположения компонента i в другой среде ( 1 - расслоенная, лентовидная, кольцевая; 2 -пузырьковая; 3 - струйная; 4 - четочная; 5 - снарядная).

Интересным моментом является кольцевая и расслоенная структуры.

Для кольцевой структуры, полагая, что компонент прижат к стенкам контрольного объема (рис. 2- а ), характерным размером - r будет толщина слоя.

а =

п [ R ² - ( R - r )²] L  R ² - ( R - r )²

niL        R в = L

2 п [ R + ( R - r )] _ R + ( R - r )

2 nRL         R

На рис. 6- б отображена теоретическая зависимость пси-фактора от толщины слоя. Как видно предельным значением, когда толщина слоя равна R пси-фактор равен 2/3.

I r I                  .

Как видно функция Y I имеет нелинейную k R j

I r I форму, а в I линейную и находится в границах

k R )

(1,2) (рис. 6- б ).

В случае расслоенной структуры характерным размером r будет расстояние от края контрольного объема (рис. 2 - б).

Y i

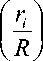
0            0.2           0.4           0.6           0.8            1

r/R,м

б)

Рис. 6. Зависимость пси-фактора и бета-фактора от относительной толщины кольцевого слоя.

_ п [ R ² - ( R - r )²] L  R ² - ( R - r )²

а      nR L         R    ’

_Л 2 п [ R + ( R - r )] ₌ R + ( R - r )

Р      2nRL        R

При лентовидной и особенно кольцевой структуре в -фактор может быть больше единицы, т.к. у кольца берется внутренняя и внешняя площадь.

В качестве вывода стоит отметить, что два выведенных фактора - а и в позволяют идентифицировать характеристику потока компонента в контрольном объеме. При этом по ним можно легко вычислить необходимые для определения силы бинарного трения через введенные функции вероятности взаимодействия компонентов.

Задача расчета изменений данных факторов вследствие гидродинамической обстановки (давление, температура, кинетические энергии, скорости, вязскости и т.п.) можно свести, как к настроечным функциям, полагая, процесс перехода от структуры к структуре мгновенным, или согласно методике, основанной на противодействии сдерживающих сил (агрегационные силы - молекулярного притяжения) и сил сегрегации (например, вследствие кинетических энергий и вязкостного трения).

Типы структур в цилиндрическом контрольном объеме

Таблица 1

Форма элемента	a	σ n = — α	в	α w = — β	о	∑ Sie	Тип структуры
						S
цилиндр	1	1	1	1	1	1	сплошная
цилиндр	<<1	>>1	>>1	0..1	<1	>>1	струйная
полый цилиндр	a = о	1	1..2	<2/3	<1	1..2	кольцевая
любая	a = о	1	<1	<<1	<1	<1	расслоенная
сфера	a = о	1	1	2/3	2/3	1	идеальная пробковая
эллипсоид	a = о	1	>2/3	2/3< w <1	2/3< о <1	>2/3	снарядная
сфера	a <<  о	>>1	<<1	<2/3	<1	>>1	пузырьковая
инверсия сфера	a <<  о	>>1	<<1	<1	<1	>>1	обратно-пузырьковая
эллипсоид	a <<  о	>>1	<<1	<1	<1	>>1	четочная

Получается, что текущее состояние элементов, выраженное в альфа и бета факторах, будет влиять

где

ST

- площадь поперечного сечения контрольно-

на новое состояние, т.к. «прочность» элементов зависит от их текущей геометрии и степени воздей-

ствия на них извне.

На основе эмпирического опыта движения жидкостей и газов в цилиндрических каналах согласно Дарси-Вейсбаха для межфазного трения можно записать виде функции перепада давления

го объема.

Важным параметром здесь является D _i , который должен включать ранее введенные факторы структуры потока компонента i .

В первом приближении определяем для компонента - D

на взаимное трение, вызванное трением компонента

j о компонент i

. = X. L-b . pi , j       i, , j        * , j

ρiρjωi-ωj(ωi-ωj)

2 D.

и действующее на каждый элемент потока i

e pi, j         *, j         *,. j

ρ _i ρ _j ω _i - ω _j ( ω _i - ω _j ) n 2 D

4 ^ V  4 о У  4 V a 4 V

D =    =1^ == w i  ∑Sie  σ βiS   S βi   S i αi

Ранее введенные настроечные эмпирические функции вероятности взаимодействия компонентов gi j (p_il , Oj ) будут оказывать влияние на коэф-

Скорость компонента - ^ =

m

Sp •

где     b i , j - коэффициент бинарного трения меж

ду компонентами;

D 1 - условный гидравлический диаметр, показывающий суммарный средний диаметр элементов потока i -го компонента ;

L - длина участка течения в контрольном объеме;

m , - текущий массовый расход компонента вдоль рассматриваемой оси;

T

S i - суммарная площадь поперечного сечения потока i -ого компонента.

Последнюю можно вычислять по-разному исходя из табл. 1.

Весьма приближенно, для сферических капель или струй

фициент сопротивления ^ *,j

1             & , j ^{( о} ° j ) D i

^ i , j = H ^{- to}j ---- 1— ---.

ν _i ν _j

Для расчета изменений в структуре потока элемента примем допущение, что форма и размер элементов сдерживается молекулярными силами сжимающими каплю (элемент потока), а сила, вызванная межфазным трением, разрушает каплю.

Для расчета капиллярного давления требуется знание характерного размера r элемента потока. Это можно сделать из соотношения трех величин

1. Боковая площадь элемента S * = S e

S T = S T о , ,

• 2.    Объем элемента V_t = a i V

• 3.    Площадь поперечного сечения элемента S e - T = о S T

Весьма приближенно, т.к. в будущем потребуется методика вычисления с учетом всех типов элементов потока

r = 1 f —+X)

i 2 ( S e    S e - ^T J

i

1 f ve   ve )  Va i—+=+

2 (SP,   ctS J  SPi

= ¹ a v ^f+

2 i (Sp   ст,ST J

Совсем примитивный вариант рассчитать средний радиус элементов, как

3 r i ^{v a} i .

Далее для расчета задаются функции давления агрегации от радиуса кривизны в виде Р , = Y i ( r ) . Вполне логично предположить, что для жидкостей функция будет близкой к гиперболе.

Для расчета изменения факторов альфа и бета введем последние эмпирические зависимости в виде относительного изменения критерия объема и a = as

формы элемента (рекурсивная формула)

V(pc -\kp[j|)r),Pi = Piфkdt(Pc -|bPej |)ri).

В качестве аргументов к функциям выступают: разность давления агрегации элементов и перепада давления на трение межу фазами умноженное на время, а также текущий характерный размер элемента.

По-сути, первый аргумент есть импульса силы, вызывающей изменение объема и формы элемента потока.

При перепаде давления на трение меньше давления агрегации функция S i j ( p • dt , r ) должна быть более, либо равна 1,0. В противном случае менее или равна 1,0, т.е. происходит дробление объема – разрушение элементов потока. Если функции единичны на всей области определения, тогда начальные значения этих факторов изменяться не будут.

Для расчета многофазного течения такие функции задаются для каждого компонента. При этом важно отметить, что для расчета изменений данных факторов требуется рассчитать все перепады давления на трение со всеми соседними фазами, т.е. как в рекурсивной формуле ниже

«,=П ai£i(dt (p,c - bpej t) r).

j = 1

Аналогичным образом для бета-фактора.

Модуль для перепада давления взят, так как не имеет значения, что происходит: торможение или разгон потока со стороны соседнего компонента. Здесь важен скаляр – сила воздействия.

Для системы продуктивных пластов в т.ч. и с трещинами [11] особенно важно учитывать меж-фазное(бинарное) трение. Последнее позволяет оценить истинную эффективность систем поддержания пластового давления [10].

Для моделей внутрипорового вязкостного межфазного трения вышеприведенную методику можно упростить.

Известно, что вязкостное трение в поровой системе (в подземной гидромеханике) определяется согласно закону Дарси с учетом кривых относительных фазовых проницаемостей bPi = LMi

vi

k • ki ⁽ ст ) ’

или

vgradPi = ц, i( . k • ki (at)

где ^ц , , <7 i , к , - динамическая вязкость, насыщенность и относительная фазовая проницаемость i-го компонента; L – длина контрольного объема; k - абсолютная проницаемость, м²; ц - скорость фильтрации, м/с.

В качестве настройки на эксперимент используются кривые ОФП, например, в виде функций k i ( ст ) (т.е. от насыщенности самого компонента).

Так как мы предполагаем учесть потери давления – градиент давления, т.е. силу межфазного бинарного трения, то в качестве вспомогательных функций введем коэффициент бинарного трения, аналогично, коэффициенту выше и коэффициент вероятности взаимодействия зависящий от текущей насыщенности взаимодействующих компонентов – g por ⁽ CT-ct J .

При этом скорость должна быть выражена через разницу истинных скоростей компонентов, а кривая ОФП здесь исключается, так как по нелепой традиции включает в себя поправку на площадь фильтрации компонента, т.е. долю его в поровом просвете.

Градиент давления, вызванный вязкостным трением компонента i о компонент j будет, согласно аналогу Дарси следующим образом

№ - to

gradPi, j =л ц^ц^, —^-bi, jgi,j"r (ct, стj),

и       uj

где № =----, № =--истинные средние ско- mCT      mCTj рости течения компонентов; bi,j - коэффициент бинарного трения, д.е.; gpoor(ст, СТ ) - функция ве" роятности бинарного взаимодействия, зависящая от структуры потока и в общем смысле от площадей соприкосновения компонентов.

Коэффициент абсолютной проницаемости введен в формулу во избежание риска преувеличения градиента давления межфазного трения над основ- ным градиентом давления. Однако такой случай вполне возможен при определенных условиях: ко-υi гда истинная скорость – ω = i будет суще-mσ ственно больше скорости фильтрации. По вязкости взято среднегеометрическое чтобы учесть взаимное трение.

Все коэффициенты бинарного трения будут зависеть от давления и температуры, т.к. температура определяет диффузию между слоями, а давление силу прижимания фаз.

Для случая внутрипорового трения все параметры контрольного объема должны учитывать коэффициент открытой пористости.

Естественно, здесь для учета размеров капилляров в поровой системе не вводятся условия изменения пси-фактора ψ , так как, по-сути, размеры поровых каналов и суммарная боковая площадь элементов потока частично учтена в коэффициенте проницаемости. Для более точного учета структуры потоков требуется изменить базовую закономерность Дарси исключением проницаемости, заменив ее на средний гидравлический диаметр поровых каналов и коэффициент структурной неоднородности, равный отношению длинны контрольного объема (ячейки, керна) к средней длине порового канала (так учитывается извилистость поровых каналов и местные сопротивления на искривление фильтрационных потоков.

При решении обратной задачи – нахождении скоростей фильтрации при заданных давлениях в смежных ячейках требуется итерационный процесс в котором выполняется следующая процедура.

• 4.    Стрекалов А.В., Хусаинов А.Т., Стрекалов В.Е. Моделирование транспортной гидравлической системы // Научно-технический журнал Нефтегазовое дело – 2014. – Том 12-3, № 3. – C. 64-69.

• 5.    Стрекалов А.В., Хусаинов А.Т., Стрекалов В.Е. Метод обращения геометрических фигур // Электронный научный журнал Нефтегазовое дело 2014. – № 2. – C. 438-450. Режим доступа: http://www.ogbus.ru/authors/StrekalovVE/StrekalovVE_2.pdf

• 6.    Грачев С.И., Стрекалов А.В., Хусаинов А.Т. Исследования каналов сверхпроводимостей межскважинного пространства // Научно-технический журнал Известия вузов. Нефть и газ. – 2016. – № 5. – С. 46-56.

• 7.    Грачев С.И., Стрекалов А.В., Хусаинов А.Т. Повышения уровня контроля и управления систем ППД посредством создания универсальной модели // Известия вузов. Нефть и газ. – 2016. – № 3. – С. 52-60.

• 8.    Стрекалов А.В., Хусаинов А.Т., Стрекалов В.Е. Метод управления технической гидросистемой посредством анализа регулировочных кривых // Электронный научный журнал Нефтегазовое дело. –  2014.  –  №  2.  –  C.14-32. Режим доступа:

• 9.    Стрекалов А.В., Хусаинов А.Т., Стрекалов В.Е. Модель течения несжимаемой и сжимаемой жидкости // Научно-технический журнал Нефтегазовое дело. – 2014. – Том 12-3, № 3. – C. 54-63.

• 10.    Стрекалов А.В., Хусаинов А.Т. Формализация задачи оптимизации систем поддержания пластового давления // Электронный научный журнал Нефтегазовое дело. – 2015. – № 3. – C. 237-255. Режим доступа: http://ogbus.ru/issues/3_2015/ogbus_3_2015_p237- 255_StrekalovAV_ru.pdf

• 11.    Грачева С.К., Стрекалов А.В., Хусаинов А.Т. Моделирование образования сети трещин ГРП // Электронный научный журнал Нефтегазовое дело. – 2013. – № 2. – C. 168-183. Режим доступа: http://www.ogbus.ru/authors/ GrachevaSK / GrachevaSK _1.pdf

• 12.    Хусаинов А.Т. Применение инструментария исскуственных нейроных сетей для оперативного расчета нефтедобычи // Научно-технический журнал Нефтегазовое дело. – 2013. – Том 11, № 2. – C. 22-25.

• 13.    Хусаинов А.Т. Методика оперативного прогнозирования показателей нефтедобычи средствами программного комплекса с аналитическим модулем искусственных нейронных сетей // Научно-технический журнал Нефтегазовое дело – 2013. – Том 11, № 3. – C. 44-51.