Принципы оценки рисковых потерь

Риск представляет собой событие, которое состоит в снижении или потере ожидаемого результата использования инвестиций, и происходит с определенной вероятностью. Рисковое событие может быть обусловлено множеством случайных и систематических факторов, в том числе и выбором неоптимального исходного решения. Вероятность является мерой возможности свершения данного события и изменяется в пределах от нуля для невозможного события до единицы – для достоверного события. Количественная оценка риска в управлении выполняется на основе прошлого опыта и интуиции с использованием статистического анализа текущей и ретроспективной информации. В связи с неполнотой и неточностью исходной информации оценка риска практически всегда имеет приближенный характер. Кроме того, на практике часто возникают ситуации, когда даже вероятностные оценки относительно будущих событий получить в принципе невозможно. Такие ситуации в общепринятой терминологии классифицируют как принятие решений в условиях неопределенности [1].

В условиях риска применяют один из следующих критериев: среднего ожидаемого значения, ожидаемого значения с учетом его возможной вариации; критерий предельного уровня и критерий наиболее вероятного (модального) исхода. На практике чаще всего используют первые два критерия, которые представляют собой естественный переход от условий полной определенности.

В отличие от ситуаций с риском в условиях неопределенности никакие вероятностные характеристики не известны. При этом в качестве количественных критериев принятия решений используют один из следующих критериев: критерий Лапласа, минимаксный критерий, критерий Сэвиджа, критерий Гурвица. Данные, необходимые для принятия решений в условиях неопределенности, обычно представляют в виде матрицы, строки которой соответствуют возможным действиям, а столбцы – возможным состояниям системы. Каждый элемент матрицы, находящийся на пересечении строк и столбцов, соответствует результату, определяющему доход или потери при выборе данного действия и реализации данного состояния. Не существует общих правил для оценки области применения каждого критерия, так как отношение лица, принимающего решение, в конкретной ситуации является определяющим фактором выбора.

Наиболее распространенным критерием принятия решений в рисковых ситуациях является критерий «среднее ожидаемое значение – вариация». Дело в том, что любые средние – это условные величины, которые используют для свертки множества случайных значений показателя в одно число. Поэтому фактические значения могут существенно отличаться от средних величин. Другими словами, разброс исходной ретроспективной информации приводит к необходимости учета рисковой надбавки. Если речь идет о доходах, то эта надбавка, естественно, должна вычитаться из среднего значения и используется нижняя граница. В про- гнозах издержек, убытков, потерь, наоборот, эта надбавка добавляется, то есть используется верхняя граница. В математической формулировке соответствующие критерии записываются в виде max(P - tap) = max(p - Лp); min(Z + taz) = min(z + Az), где P, Z - средние значения дохода или издержек соответственно;

о p , о z - стандартные отклонения дохода и издержек соответственно;

t - коэффициент кратности, зависящий от требуемого уровня доверия к результатам расчета, который определяют либо по таблицам обратного нормального распределения, либо по таблицам обратного распределения Стьюдента для случая малой выборки;

A p , A z - рисковые надбавки.

На практике очень часто встречаются случайные процессы, которые в нормальном установившемся режиме протекают во времени статистически однородно и имеют вид непрерывных случайных колебаний относительно среднего значения. Такие процессы называют стационарными. Отсюда следует, что и дисперсия и математическое ожидание для стационарных процессов должны быть постоянными. Если процессы имеют определенную тенденцию развития во времени, то они являются нестационарными. Соответственно изменяются и методы прогнозирования рисковых потерь.

В данной статье в качестве иллюстрации общих принципов принятия решений приведены Simulink -модели прогнозирования рисковых потерь на финнансовом рынке и в страховании имущественных рисков.

Современные методы оценки финансовых активов основаны на предположении, что будущая цена зависит только от ее значения в данный момент и не зависит от предыдущих значений. На практике используют биномиальные, триномиальные и броуновские модели. Наиболее распространенной является теория геометрического броуновского движения, согласно которой приращение цены dS за малый промежуток времени dt подчиняется стохастическому дифференциальному уравнению [2,3]:

dS = (rdt - qdt + as^dt) S, где e - случайное число из последовательности нормально распределенных случайных чисел со средним значением 0 и стандартным отклонением 1;

• r , о - доходность и стандартное отклонение доходности актива за расчетный период соответственно;

• q - дивидендная доходность базисного актива.

Если время считается в долях года, то r, q и о принимаются в годовом измерении, например, r = 0,2 ; q = 0,1 и о = 0,3 , а если единицей измерения времени является день, то r = 0,2/252 ; q = 0,1/252 и о = 0,3/252^0,5 , где 252 - принятое число рабочих дней.

Для получения статистически обоснованных результатов необходимо иметь сотни тысяч реализаций. Поэтому разработана простая модель в системе Matlab/Simulink , позволяющая решать множество задач, связанных с ценообразованием финансовых активов (рис. 1).

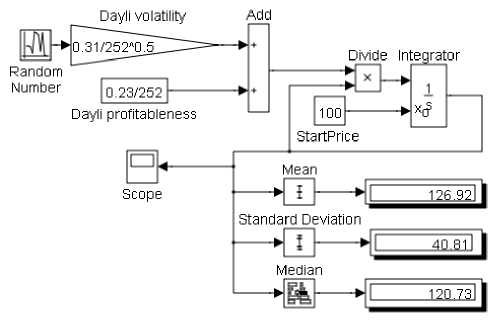
Рис. 1. Модель прогнозирования динамики цен

Модель решает стохастическое дифференциальное уравнение, приведенное выше, при заданных начальных условиях. Исходная информация (волатильность, доходность и стартовая цена) получена по данным о дневных котировках акций Сбербанка на ММВБ за предыдущие два года. Источником стандартизованных случайных чисел является блок Random Number , который при каждом запуске модели генерирует новую прямоугольную матрицу этих чисел размерностью [ m×n ], где m – заданное число дней, а n – число случайных значений для каждого дня. Выбор числа реализаций n зависит от требуемой точности и может изменяться от десяти до многих сотен тысяч, а время моделирования – от нескольких секунд до минуты. В треугольном блоке Daily volatility выполняется операция умножения дневной волатильности на случайное число. Единицей модельного времени является один день, поэтому время моделирования задается не в долях года, а в днях.

На рисунке 2 показаны сто возможных реализаций случайного процесса изменения цен в течение года, полученные с осциллографа Scope , где горизонтальная ось времени соответствует номеру рабочего дня года, а вертикальная – ценам на акцию.

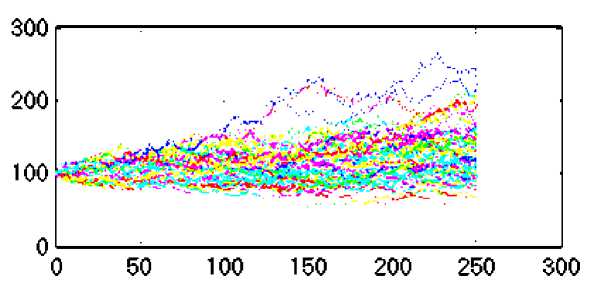
Рис. 2. Реализации случайного процесса изменения цен

Дневное распределение цен в соответствии с уравнением стохастической динамики подчиняется несимметричному логарифмически нормальному распределению, а отклонение медианы от среднего показывает степень этой асимметрии. Значение медианы 120,73 руб . означает, что в половине случаев фактическая цена будет больше этой величины, а в половине – меньше. На рисунке 3 показана гистограмма распределения цен для последнего дня года.

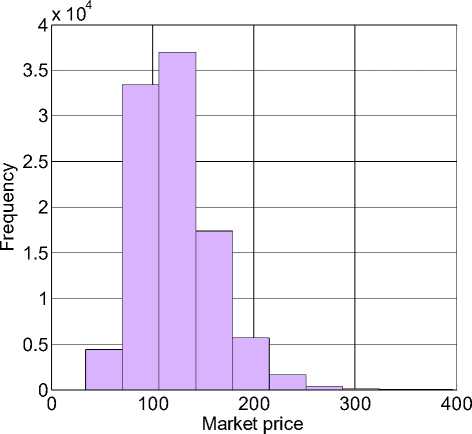
Рис. 3. Гистограмма распределения вероятной цены акции

Для оценки риска финансовых инструментов используется показатель стоимости под риском VaR ( Valua at Risk ), то есть максимально возможный убыток инвестора в денежном измерении из-за колебаний цены при заданном уровне доверительной вероятности и длительности временного периода. Данный показатель определяется, как правило, для однодневного, десятидневного или месячного периода. Величина VaR для однородного портфеля определяется как произведение стандартного отклонения для выбранного периода на коэффициент кратности нормального распределения. Коэффициенты кратности принимают 1,645 ( 95%) или 2,326 ( 99%). Например, для месячного периода, если стоимость портфеля составляет 100 тыс. д .е., то величина VаR , равная 15,05 тыс. д.е . при 95 % уровне доверия означает, что можно с 95 % вероятности утверждать, что инвестор в течение следующего месяца не потеряет более 15,05 тыс . д.е .

Модель оценки VаR приведена на рисунке 4, где в связи с достаточно большим объемом выборки ( 100 тысяч) используется нестандартный способ, не зависящий от характера распределения цен. Основная часть блок-схемы для получения множества случайных значений цены остается такой же, как и на рисунке 1.

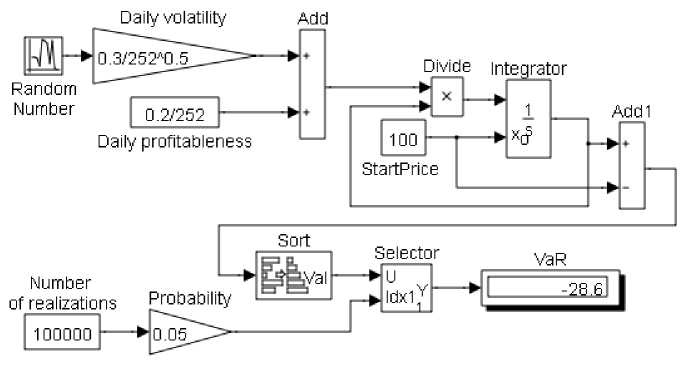
Рис. 4. Модель оценки стоимости под риском VаR

В блоке Add1 вычисляется разница между вероятными рыночными ценами и начальной ценой рискового актива. Блок Sort выполняет сортировку полученных значений по возрастанию, а блок Selektor выполняет поиск значения по заданному номеру в возрастающем вариационном ряду. Этот номер соответствует требуемой вероятности, которая указывается в блоке Probability. На дисплее показано значение VаR при доверительной вероятности 95 % для годового периода. На рисунке 5 показана динамика стоимости под риском на протяжении одного года, где на горизонтальной оси отображается время в днях, а на вертикальной – рисковая стоимость в соответствующих денежных единицах.

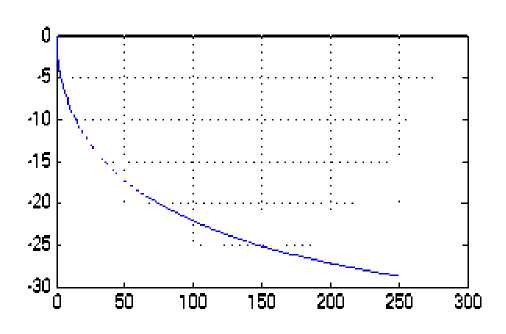
Рис. 5. Осциллограмма изменения рисковой стоимости во времени

Если требуется 99 % надежность, то в блоке Probability вместо 0,05 вводится 0,01 . Для оценки VаR портфеля вычисляется средняя доходность и волатильность на основе ковариационной матрицы составляющих активов.

В имущественном страхования тарифные ставки рассчитывают на основе накопленной статистики об убыточности страховой суммы за определенный период времени и прогноза ее на следующий год [4,5]. Нетто-ставка T N состоит из двух частей – основной части T 0 и рисковой надбавки Δ. Основная часть нетто-ставки равна убыточности страховой суммы, которая определяется как отношение страхового возмещения к страховой сумме всех застрахованных объектов для данного вида страхования. При этом используется принцип эквивалентности взаимных обязательств страховщика и страхователя: все денежные средства, полученные из расчета этой ставки, должны быть выплачены в виде страховых возмещений. Рисковая надбавка вводится для того, чтобы учесть неблагоприятные колебания показателя убыточности в будущем. Брутто-ставка T B рассчитывается по формуле T N / (1 – f), где f – доля нагрузки в структуре брутто-ставки. Нетто-ставка предназначена для формирования страхового фонда, используемого для текущих страховых выплат при наступлении страховых случаев и создания страховых резервов. Нагрузка обеспечивает поступление средств, используемых для покрытия расходов на ведение дела по страховым операциям, а также служит для формирования фонда превентивных (предупредительных) мероприятий и плановой прибыли.

На рисунке 6 показана модель для прогнозирования нетто-ставки страхового тарифа на основе накопленной информации за пять лет при заданной гарантии безопасности 0,95 , которая может использоваться для любых аналогичных процессов и любых массивов исходной информации.

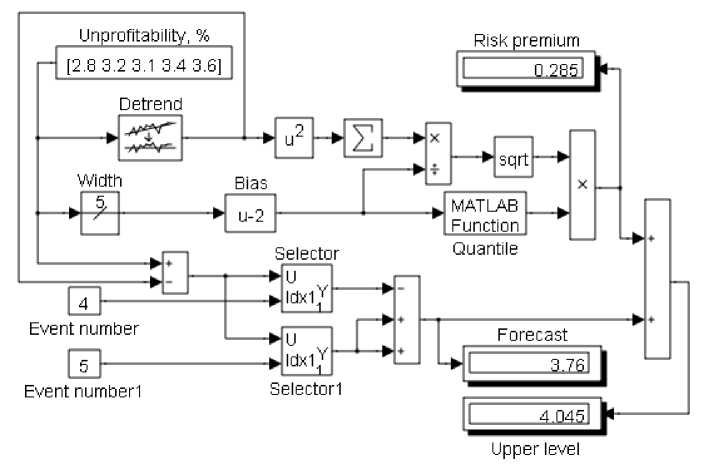
Рис. 6. Модель планирования страхового тарифа

Исходные данные показаны в блоке Unprofitability , куда они поступают из таблиц Excel . Блок Detrend удаляет линейный тренд из исходных данных, в блоке u² отклонения от линии тренда возводятся в квадрат, в блоке-сумматоре – складываются, а результат делится на число степеней свободы, которое равно размеру выборки минус два (блоки Width, Bias). Квадратный корень из полученной суммы является стандартной ошибкой выборки ( 0,121 ). Рисковая надбавка определяется как произведение квантили обратного t -распределения Стьюдента на стандартную ошибку. Квантиль рассчитывается в блоке Quantile по формуле tinv ( 0,95, u ), где u – число степеней свободы из блока Bias.

В нижней части блок-схемы выполняется расчет основной части нетто-ставки (T0), которая равна прогнозируемому уровню убыточности страховой суммы на следующий за последним период в предположении линейного тренда. Для получения сглаженной зависимости убыточности из фактических данных вычитаются отклонения от линейного тренда. С помощью селекторов выполнятся поиск двух последних известных значений сглаженной зависимости, по которым легко найти прогнозное значение на будущий период, так как абсолютные приросты линейной функции одинаковы. Сумма точечного прогноза средней убыточности и рисковой надбавки соответствует верхнему одностороннему пределу распределения, который принимается за основу страхового тарифа. Таким образом, модель позволяет мгновенно получить точечный и интервальный прогнозы любого временного ряда по линейному уравнению регрессии, которое является оптимальным для наиболее типичного на практике случая малой выборки.

Рассмотренные модели используются в учебном процессе на кафедре менеджмента и административного управления КрасГАУ и являются составной частью учебно-исследовательского комплекса визуальных моделей риск-менеджмента.