Принципы поиска диагностической функции риска

Принятие большинства управленческих решений осложняется условием многокритериальности, так как определяющих показателей, как правило, много и они меняются в противоположных направлениях. Поэтому всегда стремятся свернуть набор всех частных показателей в один комплексный количественный или качественный критерий, по значению которого делают выводы, например, о степени живучести фирмы с точки зрения потери платежеспособности. Существует множество различных методов и скоринговых функций для оценки риска дефолта предприятий, однако ни один из них не позволяет получить идеальный конечный результат [1]. В зарубежных странах широко используются факторные модели Альтмана, Бивера, Лиса, Таффлера, Чессера, Тисшоу и др. В последние годы опубликованы отечественные разработки, например, известные модели Давыдовой и Беликова, Сейфуллина-Кадыкова, Федотовой, Колышкина [2, 3]. В данной статье представлен алгоритм и результаты исследования возможности применения дискриминантной диагностической функции для оценки и прогнозирования финансового состояния сельскохозяйственного предприятия по обобщенному критерию.

Дискриминантный анализ используется с целью получения оптимального решающего правила для отнесения объекта к определенному классу, то есть по существу является инструментом для распознавания образов по набору диагностических признаков. Как правило, используются линейный дискриминантный анализ и два класса объектов, где принятие решения определяется значением линейной функции для данного объекта, в которой аргументами являются наиболее информативные признаки совокупности изучаемых объектов, а весами – оптимальные коэффициенты, получаемые в результате решения задачи дискриминации. Если полученное значение больше некоторого порогового значения дискриминантной функции, то конкретный объект относят к одному классу, а если меньше – к другому.

Дискриминантная функция по существу является уравнением линейной регрессии с размерными коэффициентами. Разница заключается лишь в том, что при вычислении коэффициентов уравнения регрессии имеется внешний критерий, а при выполнении дискриминантного анализа внешнего критерия нет. Например, при расчете регрессионного уравнения, связывающего цену и потребительские свойства товара, кроме значений показателей потребительских свойств, известны цены на товары-аналоги. При построении уравнения разделяющей функции известны значения совокупности показателей для обеих выделенных групп, а замыкающий показатель степени близости к банкротству отсутствует. Область применения дискриминантного анализа ограничена примерно теми же требованиями, что и для регрессионного анализа:

• ■    линейная независимость между признаками, то есть ни один из признаков не должен быть линейной комбинацией других признаков;

• ■    нормальный закон распределения значений признаков;

• ■    число объектов для анализа должно превышать число признаков не менее чем на две единицы.

Алгоритм выполнения дискриминантного анализа рассмотрим на конкретном примере. В качестве определяющих признаков выбраны следующие коэффициенты:

• К 1 – собственный оборотный капитал / сумма активов;

• К 2 – нераспределенная прибыль / сумма активов;

• К 3 – прибыль до выплаты процентов и налогов / сумма активов.

Данные по двум группам из 15 предприятий в каждой группе представлены в табл. 1.

Исходные данные по группам предприятий

Таблица 1

Устойчивое предприятие			Кризисное предприятие
К 1	К 2	К 3	К 1	К 2	К 3
0,48	0,77	0,22	-0,06	-0,55	-0,20
0,77	0,61	0,37	-0,08	-1,06	-0,42
0,64	0,57	0,16	-0,05	-0,72	-0,22
0,65	0,11	0,13	-0,02	-0,39	-0,22
0,48	0,24	0,13	-0,02	-0,43	-0,27
0,08	0,10	0,15	-0,01	-0,77	-0,21
0,43	0,26	0,09	-0,11	-1,22	-0,58
0,04	0,36	0,16	-0,06	-1,38	-0,32
0,42	0,27	0,23	-0,03	-0,35	-0,38
0,62	0,31	0,33	-0,08	-0,40	-0,06
0,25	0,32	-0,02	-0,07	0,15	-0,23
0,62	0,43	0,07	-0,09	-0,61	-0,32
0,54	0,49	0,09	-0,10	-0,35	-0,40
-0,07	0,05	0,11	-0,08	-0,96	-0,69
0,27	0,41	0,10	-0,07	-0,35	-0,25

Следует сразу отметить, что одной из главных проблем анализа является отбор наиболее информативных признаков изучаемого множества объектов. Для получения наилучших различий используются критерии последовательного отбора признаков или пошаговый дискриминантный анализ [4, 5]. По обеим обучающим выборкам рассчитываем векторы-строки средних значений показателей.

Вектор-строка средних значений показателей для устойчивых, то есть благополучных предприятий X 1 :

[0,414 0,355 0,154] .

Вектор-строка средних значений показателей для кризисных, то есть неблагополучных предприятий X 2 :

[ - 0,061 - 0,628 - 0,318] .

Рассчитываем ковариационную матрицу для устойчивых предприятий D 1 :

0,062 0,025 0,010

0,025 0,040 0,006

0,010 0,006 0,010

Рассчитываем ковариационную матрицу для кризисных предприятий D 2 :

0,001 0,002 0,002

0,002 0,160 0,032

0,002 0,032 0,026

При определении матриц ковариаций в электронных таблицах следует иметь в виду, что с помощью инструмента для расчета ковариации пакета анализа получается результат для генеральной совокупности, а не по выборке, поэтому все значения следует помножить на отношение n / (n-1).

Далее надо объединить обе матрицы в одну, то есть найти общую матрицу D y по формуле:

D y = [n i D i + n 2 D 2 ]/(n i + П 2 -2), где n i , П 2 - объемы выборок для первой и второй групп; D i , D 2 - ковариационные матрицы по обеим группам.

В результате весового суммирования элементов обеих матриц получаем суммарную матрицу D у :

0,034 0,015 0,006

0,015 0,107 0,020 .

0,006 0,020 0,019

Рассчитываем обратную матрицу D y^- :

“ 32,16   - 2,96    - 7,59 ’

• - 2,96  11,98   - 11,80 .

• - 7,59 - 11,80 67,58

Находим разность векторов средник значений показателей путем вычитания из средних по группе благополучных предприятий средних по кризисным предприятиям (X₁ - X₂):

[0,475 0,981 0,472] .

В результате умножения полученной вектор-строки разностей средних значений показателей на обратную матрицу получаем оптимальные весовые коэффициенты дискриминантной функции:

[8,790 4,777 16,715] .

Чтобы изменить масштаб коэффициентов этой функции можно использовать любые способы нормировки при соблюдении условия пропорциональности. Например, можно сложить полученные коэффициенты, извлечь квадратный корень из суммы и каждый коэффициент разделить на это значение. Тогда получим разделяющую функцию с такими же свойствами, что и исходная функция, но другого масштаба. Для дальнейших вычислений использованы коэффициенты, полученные именно таким образом:

[1,597 0,868 3,037] .

Выполненные исследования показывают, что существует универсальный критерий для поиска оптимальных весовых коэффициентов с использованием алгоритма нелинейного программирования: максимум отношения ожидаемой разности средних по группам предприятий к общему стандартному отклонению.

Другими словами, числитель целевой функции – это вектор разности средних значений показателей, а знаменатель - корень квадратный из суммарной дисперсии, определяемой по формуле: X T * D y * X , где Х Т - транспонированный вектор искомых весовых коэффициентов дискриминантной функции ; D y - общая ковариационная матрица.

При использовании инструмента для поиска решений можно задавать любые условия на сумму и знаки коэффициентов или не использовать никаких ограничений. В последнем случае получим следующие оптимальные значения коэффициентов классифицирующей функции, которые, естественно, пропорциональны исходным значениям:

[0,872 0,474 1,658] .

Следует отметить, что в результате оптимизации при любых дополнительных условиях, накладываемых на весовые коэффициенты, оптимальное значение целевой функции равно расстоянию Махалонобиса между выборками d, которое определяется как корень квадратный из произведения вектора разности сред- них по выборкам на обратную ковариационную матрицу и на транспонированный вектор разности средних равно 4,09:

d = ^( X 1 - X 2 ) D -- ( X 1 - X 2 ) T .

Расстояние (метрика) Махалонобиса определяет качество дискриминации объектов, чем больше это расстояние, тем больше разница между выборками или объектами по совокупности выбранных показателей.

Для получения разделяющей границы рассчитываем значения дискриминантной функции для каждого объекта по обеим выборкам и определяем основные статистические характеристики для каждой группы, приведенные в табл. 2.

Статистические показатели распределений

Таблица 2

Показатель	Устойчивое предприятие	Кризисное предприятие
Среднее	1,437	-1,607
Медиана	1,520	-1,351
Стандартное отклонение	0,692	0,744
Эксцесс	0,084	-0,040
Асимметричность	0,328	-0,858
Интервал	2,634	2,407
Минимум	0,267	-3,060
Максимум	2,901	-0,653

Медиана, эксцесс и асимметричность характеризуют соответствие полученного эмпирического распределения нормальному закону. Для стандартного распределения медиана и среднее значение должны быть примерно одинаковы, а эксцесс и асимметрия (скос) близки к нулю. Знак эксцесса характеризует отклонение от теоретической кривой по вертикали. При положительных значениях распределение более островершинное, а при отрицательных – более пологое. Асимметричность характеризует смещение распределения относительно среднего значения. При положительных коэффициентах кривая скошена вправо, а при отрицательных – влево. Сравнительно малые значения эксцесса и скоса не позволяют опровергнуть гипотезу о нормальности распределений.

Зная средние арифметические значения и стандартные отклонения, можно построить теоретические плотности распределения значений дискриминантной функции для кризисных и устойчивых предприятий (рис. 1).

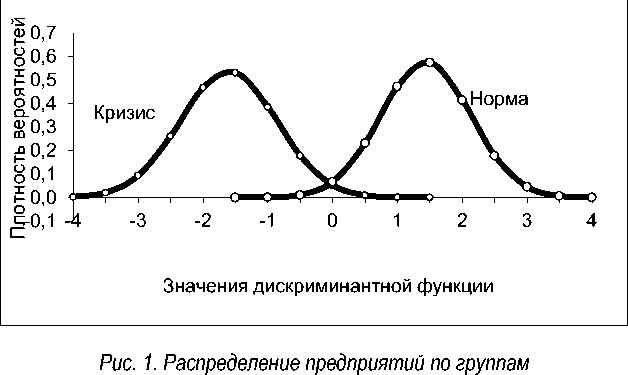
Даже без дополнительных расчетов можно видеть, что разделяющая граница соответствует примерно нулевому значению дискриминантной функции.

Если полученное значение больше 1, то предприятие следует отнести к финансово устойчивым предприятиям по совокупности выбранных признаков, а если меньше (–1), то предприятию грозит банкротство.

Точное значение разделяющей границы можно получить на основе принципа пропорциональности по

любой из следующих формул: r        m2 - mi C = m1 - o\ —---1. ^1 + ^2 ; г      , m2 - mi C = m 2 + ct2 —2----1-

σ1 , σ2 – стандартные отклонения значений дискриминантной функции для устойчивых и кризисных предприятий соответственно.

Подставив в приведенные формулы фактические значения, получим:

C = 1,437 - 0,692

1,437 +1,607

-0,03_;

-0,03

.

0,692 + 0,744

C = -1,607 + 0,744

1,437 +1,607

0,692 + 0,744

Для расчета предельных значений дискриминантной функции необходимо к среднему значению по соответствующей группе предприятий прибавить рисковую надбавку, равную произведению коэффициента кратности для нормального распределения при заданной надежности оценки на стандартное отклонение.

Тогда верхняя граница, при равенстве или превышении которой предприятия следует отнести к безусловно устойчивым, определяется из соотношения:-1,607+3,5×0,744 = 0,9998, а нижняя граница, при равенстве или меньше которой предприятия следует отнести к безусловно неблагополучным, определяется из аналогичного соотношения: 1,437–3,5×0,692 = -0,986. Коэффициент кратности принят равным 3,5, что для нормального распределения соответствует надежности 0,99977, то есть практически 100 %. Таким образом, принимаем окончательные решающие правила, приведенные в табл. 3.

Пороговые значения функции риска для расчетного примера

Таблица 3

Значение функции риска Z	Вероятность банкротства
Z < = –1	Очень высокая
–1 < Z < 0	Высокая
0 < Z < 1	Низкая
Z > = 1	Очень низкая

В практических расчетах распределение значений дискриминантных функций может иметь самый различный вид. На рисунках 2–3 показаны реальные функции распределения, полученные по двум группам сельскохозяйственных предприятий Красноярского края.

Распределение предприятий

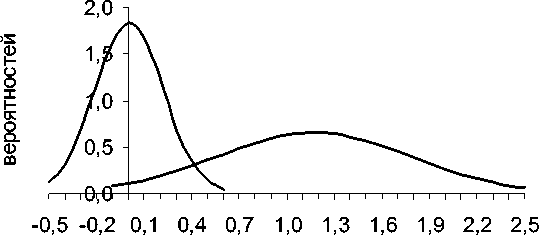
Дискриминантная функция

Рис. 2. Дифференциальные функции распределения

Кроме плотностей распределения показаны также интегральные функции (рис. 3), которые показывают вероятность превышения заданного значения дискриминантной функции для кризисных предприятий и вероятность непревышения заданного значения для устойчиво работающих предприятий. Следует отметить, что разделяющая граница определяется не точкой пересечения кривых плотности распределения, а точкой пересечения интегральных функций.

Накопленные вероятности

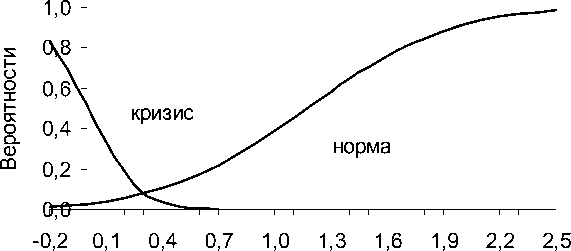
Дискриминантная функция

Рис. 3. Интегральные функции распределения

На рисунке 3 видно, что разделяющая граница равна значению 0,3, а на рис. 2 кривые пересекаются при большем значении дискриминантной функции. Для автоматизации вычислений при наличии релевантной информации целесообразно использовать соответствующие инструменты в системах Statistics или Matlab/Simulink.

Выполненные исследования позволяют сделать вывод о возможности использования методов распознавания образов для оценки и прогнозирования живучести сельскохозяйственного предприятия по совокупности признаков текущего состояния. Своевременная диагностика экономических проблем позволяет избежать финансовой неустойчивости за счет внедрения превентивных мероприятий, направленных на ликвидацию неблагоприятных тенденций, а приведенные результаты можно использовать для поддержки упреждающих управленческих решений.

Научная новизна работы, по мнению авторов, состоит в том, что получен универсальный критерий для поиска оптимальных весовых коэффициентов дискриминантной диагностической функции с использованием алгоритма нелинейного программирования: максимум отношения ожидаемой разности средних значений частных показателей по группам предприятий к общему стандартному отклонению. Предлагаемый критерий оптимизации позволяет существенно снизить трудоемкость вычислений и сделать их более прозрачными.