Принципы вероятностного анализа балансировки гибких роторов турбокомпрессоров

Обычно ротор выполняется в виде осесимметричного тела, ось симметрии которого совпадает с осью вращения. Казалось бы, подобные тела не должны иметь дисбаланса, и, следовательно, при вращении не может возникать динамических реакций. Однако в результате различных случайных погрешностей изготовления и сборки, неоднородности материала и по ряду других причин всегда имеются небольшие отклонения от идеальной геометрии [1, 2, 4-7]. Именно они и являются причиной дисбаланса.

В силу таких погрешностей каждая из образующих поверхностей изделия выполняется с некоторыми радиальными или торцевыми биениями, а центры масс соответствующих объемов – с радиальными отклонениями (эксцентриситетами) относительно оси вращения.

К числу таких (первичных) погрешностей относятся биения технологической базы, используемой в процессе обработки, относительно конструкционной, биение обрабатываемой поверхности, связанное с неравномерностью припуска на обработку, биения, вызываемые погрешностями изготовления технологической оснастки, и другие [1, 3, 5-6]. Сюда же следует отнести и многочисленные погрешности центрирования деталей ротора, неизбежно возникающие при сборке.

Таким образом, значение статического дисбаланса роторного узла определится как векторная сумма:

v

U = 22 mj (1) ji где j соответствует виду погрешности; i – номер одного из выделенных объемов; mi, £- - массы и эксцентриситеты объемов.

Соотношение (1) имеет важное значение в

задачах вероятностного анализа и прогнозирования дисбаланса.

Целью вероятностного анализа неуравновешенности роторов является [1, 3, 5-6]:

• -    выделение некоторой совокупности случайных величин (погрешностей механической обработки деталей, сборки ротора и центрирования валопровода, температурных деформаций, оказывающих наибольшее влияние на величину дисбаланса;

• -    изыскание конструктивных технологических путей снижения уровня дисбаланса;

• -    исследование законов распределения плотностей вероятностей для основных количествен-

• ных характеристик неуравновешенности, а также динамических реакций изделия на эту неуравновешенность.

Особое значение в вопросах вероятностного анализа и расчета дисбалансов имеет закон распределения Релея. Как известно, с таким распре- делением связаны задачи, которые приводят к исследованию вероятности попадания случайной точки в круг радиуса р при условии, что координаты указанной точки (х, у) являются независимыми нормально распределенными случайными величинами со среднеквадратичны ми отклонениями <с(х) = с(у) = ст и математи

-

-

ческими ожиданиями, равными нулю:

m (x) = m (y) = 0.

При такой постановке задачи интегральная и дифференциальная функции распределения вероятностей случайной величины р >  0 определяются формулами:

F ( р ) = 1 - exp

(    2 Л

- ^ц

Та 2

V 2а 7

;

( г 7 — Та ²

V ^{2 а} 7

f (Р ) = F '(Р ) = р exP а 2

Параметр распределения а и другие числовые характеристики - мода Ц , математическое ожидание и среднеквадратическое отклонение – связаны здесь соотношениями:

Ц = а; m(р) = 1,25а ; ст(р) = 0,655а.

Линейная функция от системы случайных векторов Р 1 ...р _п , имеющих релеевское распределение:

r

R = 2 A i P i , подчиняется тому же распределению с параметром:

случаях подчиняются распределению Релея с параметрами [1, 5-7, 9]:

_n 0,5

а г = 0,5 2 r²

V     i = 1    7

(_ а 2 =^ 0,

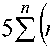
i = 1

;

\>0,5

+ ^2 )

а[R ] =

2 А2а 2 (Pi)

0,5

i

Пусть P ₀ – вероятность того, что значение случайной величины р , имеющей релеевское распределение, выйдет за пределы некоторого интервала 0 <  р <  р ₀ . Тогда

г

^Р0 = exP

V

А1

2 а ² )

.   = а 2ln —

; 0                               .

P ₀

Принимая р о = К а ( р ) , где К - некоторый коэффициент, значением которого можно варь-

ировать, найдем K = 2ln— .

P 0

Значения вероятностей P ₀ , полученных при различных К приведены в таблице.

Как видно из табл., для случайной величины, подчиняющейся закону распределения Ре-лея, практически все поле рассеивания, с точностью до долей процента, укладывается в интервале 0...3,5 а .

Отметим три наиболее важные для задач прогнозирования дисбалансов схемы суммирования компланарных векторных величин [1, 5-7, 9].

• 1.    Фазы слагаемых векторов r_i распределены по закону равномерной плотности в интервале 0...2 п , а модули детерминированы.

• 2.    Модули слагаемых векторов являются независимыми случайными величинами, а фазы равно распределены в указанном выше интервале.

• 3.    Фазы слагаемых векторов детерминированы и соответствуют точкам деления окружности на некоторое число равных частей, а модули – нормально распределенные случайные величины с одинаковыми математическими ожиданиями и среднеквадратическими отношениями: m ( r ), ( т ( r ) .

Модули суммарных векторов во всех этих

а ₃ = [ 0,5 и ст ² ( r ) ]° , .

С необходимостью вероятностной оценки эффективности низкочастотной балансировки мы сталкиваемся в следующих случаях:

• -    при выборе и обосновании метода балансировки для изделий, находящихся на стадии проектирования и отработки технологии;

• -    при оценке эффективности балансировки роторов, например, диско-барабанного типа, конструкция которых не позволяет выполнить детерминирование начального дисбаланса по результатам каких-либо измерений на низкочастотных балансировочных станках.

Во всех этих случаях эффективность низкочастотной балансировки представляется некоторой вероятностной характеристикой, определяемой, например, значением предельного (т.е. отвечающего заданной вероятности) уровня вибрации, возбуждаемой остаточным дисбалансом, или долей роторов из некоторой выборки, для которых уровень вибрации оставался бы в пределах установленной нормы. Таким образом, речь идет о некоторой среднестатистической оценке эффективности низкочастотной балансировки. Такая оценка может быть получена на основании данных вероятностного расчета начального и остаточного дисбалансов [1, 5-7, 9]. В данном случае мы рассматриваем эффективность низкочастотной балансировки гибкого ротора с центральным валом. Методика такой балансировки приведена в [4].

Следует учесть, что динамический расчет полноразмерного изделия может оказаться чрезвычайно сложным и недостаточно надежным вследствие неточной информации относительно большого числа исходных данных. Эту трудность можно избежать, если определять относительную эффективность низкочастотной балансировки не в условиях полноразмерного изделия, а для ротора, установленного на абсолютно жестких опорах [1, 5-7, 9]. Тогда в качестве критериев эффективности могут высту-

Таблица. Значения вероятностей P ₀

К	1,5	2,0	2,5	3,0	3,5	4,0
P 0	0,324	0,135	0,044	0,011	0,0022	0,0003

пать коэффициенты, отражающие степень снижения динамических прогибов или реакций, достигаемую в результате балансировки.

В соответствии с данными, приведенными в [1, 3, 4-6] примем, что статические ( U j ) или моментные ( V j ) дисбалансы каждого диска, являясь случайными по своей природе, подчиняются закону распределения Релея с одинаковыми для всех дисков параметрами:

где a j и P ij - статические коэффициенты по-

датливости.

Отсюда будут найдены искомые прогибы r m , h m 0 ( m e n ), соответствующие предельным статическому и моментному дисбалансам j-го диска для неотбалансированнного ротора. Рас-

чет по (3) повторяется n раз, причем дисбалансы U j , V j последовательно приписываются пер-

P ^(U ) = “ U n ^exp l a (U )     I

U I; P(V ) = V exp 2 a ² ( U ) J          a (V ) 4

V ² ] 2 a ² ( V ) )

вому, второму и т.д. дискам, после чего суммарное значение предельного прогиба в точке m

определяется так:

Тогда динамические реакции опор ротора и его прогибы, выраженные в виде линейных функций указанных дисбалансов, будут подчиняться тому же закону.

Пусть a ( r m ) , a ( r m о ) - параметры распределений вероятностей прогибов в некоторой точ-

r m ( го ) =

f rr/o^))2 +(hjmо(ro))2

j = 1

о.5

ке контроля, полученные, соответственно, для отбалансированного и неотбалансированного ротора. Тогда эффективность балансировки

Рассмотрим теперь ротор, отбалансированный в (N+2) плоскостях коррекции с учетом условий устранения динамических прогибов в точках p и q. Здесь динамические прогибы r m ( го о ) , h m ( го о ) для заданной угловой скорости будут найдены из уравнений:

можно оценить отношением:

Ym = a(rm )/ a(rm0 )•          (2)

Далее примем во внимание следующее. При

релеевском распределении предельное значение случайной величины, отвечающее заданной вероятности, прямо пропорционально параметру распределения. Если Ф о есть вероятность того, что случайная величина Х, имеющая релеевское распределение, выйдет за пределы отрезка [0; x о ], то величины Ф о и x о будут связаны соот

n 1                      n 1

f D kj =^{- U}j ^; f D kj x k =^{- U}j^xj ^;

kk

₂ ^{n          n}^          ₂ ⁽⁴⁾

r ^{- го} о f m s^rs ^a is ^{- го} о f D kj ^a ik = ^roo ^Uj ^a j .

s = 1                  k = 1

ношением: x о = a ( Х ) д/2ln(1/ Ф о) . Например,

при Ф о =0,0022 x о =3,5 a ( x ) . Учитывая данное соображение, можно заменить выражение (2) следующим образом: Y _m = r m / r m , где r m , r m – предельные прогибы в точке m, отвечающие

заданной вероятности.

Пусть U j , V j (j=1,2...n) – предельные значения статического и моментного дисбалансов j-го диска; D_k j , G_k j – соответствующие им дисбалансы корректирующих масс, полученные при заданном способе балансировки (k=1,2...n₁, n₁ – число плоскостей коррекции). Обозначим далее r jm ) , h (m - предельные значения прогибов, возбуждаемые дисбалансами U j , V j , соответственно, в некоторой m-й точке контроля. Для их расчета воспользуемся системами уравнений:

n1

f G kj = ^о; f G kj x k = ^- G j ^;

kk

2 n                 2 П1               2

hi — гоо f mshsais — гоо f Gkjaik = гоо Vj^ij s=1

где i , s = 1,2... n ; k = 1,2... n 1 ; го _о - расчетная угловая скорость, для которой выполняются заданные динамические условия: r p ( го о ) = r ^ ( го о ) = о , ^hp ^{( го} о ) = ^hq ^{( го} о ) = ^о , и которая соответствует максимальной эксплуатационной частоте вращения.

Расчет по (4) и (5) повторяется n раз отдельно для каждого из дисбалансов U j , V j , и в результате будут найдены соответствующие им корректирующие массы D_k j , G_k j . На следующем этапе определяются динамические прогибы r m ( го ) , h m ( го ) для отбалансированного ротора в заданном диапазоне угловых скоростей с помощью уравнений:

2 n-             2_TT

ri- to f msrsais = to Ujaij ;

s = 1

i , s = 1,2... n ;

^ri ^{(гo )— го} 2 f m s r s ( to^ is = ^го 2 s = 1

ⁿ 1

^Uj ^a ij ⁺ f D kj ^a ik k = 1

^; (6)

;

n

hi (го)—го2 f mshs (to)ais = го s=1

ⁿ 1

V j P j + f G kj a ik k = 1

, (7)

2 n             2tz

hi- го f mA a = го уд; I s=1                           f i, s = 1,2... n;                      I

причем го e Ю; гоо ]

i , s = 1,2... n ; k = 1,2... П 1 ;

,

Расчет по (6) и (7) повторяется для каждого из указанных дисбалансов, после чего находим

суммарное значение предельного прогиба в заданной контрольной точке и для заданной угловой скорости:

r m ( о ) =

² [ ( r m ПУ + ^П)²

j = 1

0.5

Далее рассчитывается коэффициент эффективности балансировки:

Y m ( о ) = r m ( о )! r m ( ю ) .        (8)

Аналогично выполняется вероятностная оценка эффективности балансировки по базовой технологии. Такая оценка представляется чрезвычайно важной, т.к. она позволяет сделать вывод о целесообразности перехода на новый комбинированный способ балансировки в (N+2) плоскостях коррекции.

Базовая технология включает в себя следующие операции [1, 4-7, 9]: балансировка центрального вала в сборе с коррекцией дисбаланса за счет съема материала в двух заранее оговоренных плоскостях; сборка и балансировка первого промежуточного балансировочного узла, включающего в себя вал и два смежных рабочих колеса компрессора; сборка и балансировка второго, третьего и т.д. промежуточных балансировочных узлов, причем каждый последующий узел отличается от предыдущего двумя дополнительными смежными рабочими колесами. При этом, в отличие от предлагаемой технологии, на каждом этапе выполняется не только измерение, но и коррекция дисбалансов в плоскостях, которые проходят через центры масс вновь устанавливаемых колес.

При базовой технологии статические дисбалансы колес устраняются из числа факторов, вызывающих динамический прогиб. Однако такими факторами остаются моментные дисбалансы и связанные с ними соответствующие корректирующие массы.

Пусть k – номер балансируемого узла, (2k-1) и 2k – номера образующих этот узел рабочих колес (нумерация ведется от левой опоры) Тогда прогибы, создаваемые моментным дисбалансом (2k-1) колеса и соответствующих ему корректирующих масс определяются из уравнений: h -о² n m_sh_sa = ^V'в + ^a i,²k ^ 2k ^{- 1} ^

i            S S IS         ri,2k — 1                       ,(9)

s=1                V                 lk       J причем i, s = 1,2...n ; lk - расстояние между центрами масс указанных колес.

Динамические прогибы от моментного дисбаланса 2k колеса будут найдены аналогично:

2 n         2i ^ ^k ^a -2 k — 1

h i ^ю ^ m i_shs ^a s = to V ^в 2k k . +              , (10)

s=1                V              lk       J причем V – предельное (с заданной вероятнос- тью) значение моментного дисбаланса, принимаемое здесь для всех дисков одинаковым.

Из уравнений (9) и (10) найдем прогибы h_m 2 k - 1 и h m 2k , т.е. прогибы в m-й точке контроля, создаваемые моментными дисбалансами колес (2k-1) и 2k, соответственно. Суммарный прогиб, создаваемый всеми моментными дисбалансами будет равен:

г rm

n^u

2 ( h m , 2 k — 1

k = 1

⁺ h m ² ,2 k

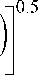
Далее определяется коэффициент эффективности Y m ( о ) по (8).

На рис. 1 изображены графики зависимостей Y m ( ю ) построенные по результатам расчета, проводимого для базовой (кривая 1) и для предлагаемой технологиям (кривая 2) для роторов компрессорных агрегатов “Синтезгаз” 103J463B5 (рис. 1), 2BCL-306а (рис. 2). Предельные значения моментного и статического дисбалансов были приняты равными V=10^-4кг·м² и U=10^-4кг·м. Точка контроля прогибов принималась на расстоянии 0,4 l от левой опоры.

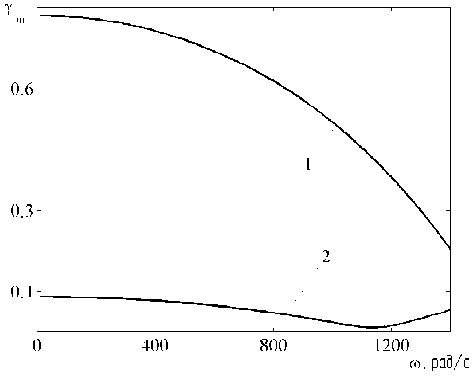
Рис. 1. Результаты расчета Y m ( ю ) для ротора турбокомпрессора 103J463B5

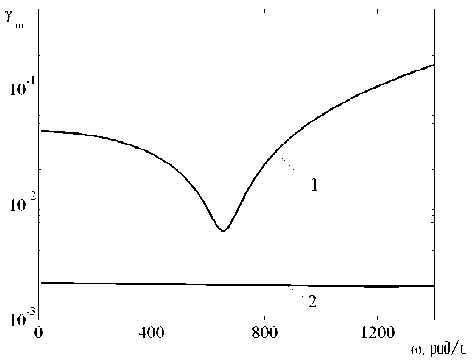
Рис. 2. Результаты расчета Y m ( ю ) для ротора турбокомпрессора 2BCL-306а

ВЫВОДЫ

• 1.    Из анализа приведенных результатов можно заключить, что эффективность балансировки в (N+2) плоскостях коррекции значительно превышает эффективность, достигаемую по базовой технологии. При этом трудоемкость предлагаемых методов балансировки заметно меньше, по сравнению с базовой технологией. Все это позволяет сделать вывод о целесообразности перехода на новые способы уравновешивания, которые способствуют существенному снижению виброактивности роторных систем и, кроме того, заметно снижают трудоемкость балансировки.

• 2.    Во всех указанных выше случаях эффективность низкочастотной балансировки представляется некоторой вероятностной характеристикой, определяемой, значением предельного (т.е. отвечающего заданной вероятности) уровня вибрации, возбуждаемой остаточным дисбалансом, или долей роторов из некоторой выборки, для которых уровень вибрации оставался бы в пределах установленной нормы. Таким образом, вероятностная оценка эффективности балансировки может быть получена на основании данных вероятностного расчета начального и остаточного дисбалансов.

• 3.    Динамический расчет полноразмерного изделия оказывается чрезвычайно сложным и недостаточно надежным вследствие неточной информации относительно большого числа исходных данных. Эту трудность можно избежать, если определять относительную эффективность низкочастотной балансировки не в условиях полноразмерного изделия, а для ротора, установленного на абсолютно жестких опорах. Тогда в качестве критериев эффективности могут выс-

• тупать коэффициенты, отражающие степень снижения динамических прогибов или реакций, достигаемую в результате балансировки.