Принятие проектных решений на основе модели «Ситуация-стратегия управления-действие» для модернизации системы физической защиты

Проектирование сложных технических систем, таких как системы физической защиты (СФЗ) объектов, это сложный многоуровневый процесс, заключающийся в построении оптимальной системы, способной максимально использовать свои ресурсы. Учитывая степень важности и повсеместное распространение систем физической защиты для охраны различных объектов, необходимо развивать относящуюся к ним категорию систем автоматизации проектирования (САПР). Однако до сих пор не создавался инструмент, который не просто моделирует определенные процессы в данной системе, но и проектирует СФЗ на всех ее уровнях.

В настоящее время работы в основном сосредоточены на моделировании уже существующей СФЗ для проверки ее эффективности и устранения ошибок. Один из этапов процесса проектирования предполагает определение необходимых действий, которые могут потребоваться при структурных изменениях объекта, или ухудшении обстановки в регионе, то есть смене модели нарушителя, или при изменении критерия, определяющего необходимый уровень защищенности объектов данной категории [1-2].

Так как вариантов возможных изменений структуры СФЗ может быть очень много, то сама процедура принятия решений об оптимальности СФЗ может стать трудоемкой и неэффективной. Таким образом, необходимо упростить этап принятия решений для определения действий при будущих изменениях СФЗ. Если требуемый уровень защищенности считать конечной целью предполагаемых действий или конечным состоянием объекта, то начальное состояние объекта – это текущий уровень защиты, который может быть определен экспертами. Соответственно, работу по коррекции состава СФЗ можно определить как процесс перехода между начальным и конечным состояниями. Этот процесс может быть реализован различными способами или путями, среди которых необходимо найти наилучший по каким-либо критериям путь.

В модели комплексной оценки системы защиты информации [3] используется метод, позволяющий оценить степень выполнения требований по защите информации через анализ профиля безопасности. Метод основан на построении матриц оценок в виде набора лингвистических переменных, содержащих ответы экспертов на вопросы о текущем и требуемом уровне защищенности. Далее проводится сравнение требуемого профиля безопасности с имеющимся профилем безопасности. Метод позволяет определить необходимые действия для достижения требуемого уровня защищенности, однако в нем отсутствует определение наилучшего из возможных, например, экономически выгодного пути или последовательности действий приводящей к устранению недостатков. Для определения наилучшего пути можно использовать модель «ситуация – стратегия управления – действие» (С-СУ-Д), осуществляющую поиск стратегии управления по нечетким ситуационным сетям (НСС) [4].

Методика построения нечеткой ситуационной сети

Определение наилучшего пути с использованием модели С-СУ-Д включает в себя два этапа. Вначале строится нечеткая ситуационная сеть для исследуемого объекта, а затем по готовой НСС проводится поиск стратегии управления.

Рассмотрим обратный метод построения нечеткой ситуационной сети. Метод состоит в том, что в виде графа задается отношение на множестве эталонных нечетких ситуаций si (i Є I = {1; 2 ... n}). Граф будет отражать возможные переходы из одной нечеткой ситуации в другую. Далее определяются требуемые для каждого перехода управляющие решения Rj (j Є P = {1; 2 ... f}) и степени предпочтения их применения α(si, Rj). Степень предпочтения применения управляющего решения выбирается экспертами. Критериями выбора экспертов могут быть любые параметры, связанные с требуемыми для осуществления управляющего решения мероприятиями, например, стоимость или время необходимых изменений [4].

Обратный метод построения НСС должен использоваться только для объектов, обладающих взаимной независимостью значений признаков (изменение значения любого признака не влияет на остальные). Тогда для построения НСС можно применить отношение общности ситуаций.

Дадим определение нечеткой общности ситуаций. Нечеткой (p – q)-общностью ситуаций называют такое сходство ситуаций, когда нечеткие значения всех признаков в ситуациях нечетко равны, кроме нечетких значений не более чем q признаков. Если ситуации s1 и s2 описываются p признаками, то для (p – q)-общности достаточно нечеткого равенства p – q признаков. Если значения признаков в ситуациях не зависят друг от друга, то из ситуации s1 можно перейти в любую ситуацию s2, имеющую (p – q)-общность с ситуацией s1, применением не более чем q действующих на значение только одного признака управлений [4].

Если нечеткие ситуации определяются как

Si = {}, S2 = {<Му)/у>}, у с У, (1) то степень (р - д)-общности kp.q (sb s2) ситуаций Si и s2 определяется выражением

kp-q (Si, s2) =

yey\Yq.                (2)

Признак yk принадлежит Yq, если μ(μs1(yk), μs2(yk)) < t. Считается, что ситуации s1 и s2 имеют (p – q)-общность, если степень общности не меньше заданного порога: kp-q (s1, s2) ≥ t [4].

Если ситуации si и sj имеют так называемую (p – q)-общность, то можно перейти из ситуации si в ситуацию sj, применяя не более q управляющих решений, действующих на нечеткое значение только одного признака (или однолокальных). Обычно при построении НСС пользуются отношением (p – 1)-общности ситуаций. Если ситуации si и sj имеют (p – 1)-общность, то, применив не более одного однолокального управления, можно перейти из ситуации si в ситуацию sj и наоборот.

Таким образом, граф НСС будет строиться как граф (p – 1)-общности эталонных ситуаций. Любые его две вершины будут соединены дугой, только если ситуации в вершинах имеют (p – 1) -общность по признакам. Каждая дуга (si, sj) в графе переходов между ситуациями si и sj должна быть отмечена управляющим решением R, необходимым для перехода из si в sj.

Управляющие решения определяют преобразования значений признаков ситуации, то есть по значению переменной решения и начальному значению признака можно с определенной вероятностью определить конечное значение признака. Таким образом, каждому терму лингвистических переменных решений может быть поставлена в соответствие матрица, описывающая силу воздействия значения управляющего решения. Матрица представляет собой отношение на терм-множестве изменяемого признака. Для каждого отношения значений определяется вероятность перехода из начального значения признака в конечное при воздействии рассматриваемого управляющего решения [4].

Обычно задаются некоторые стандартные управляющие решения, не связанные с конкретными ситуациями, и их матрицы. В процессе создания НСС любое требуемое управляющее решение можно определить через матрицу нечеткого отношения, задающего данное решение, к которой применяют операцию разложения по матрицам, описывающим стандартные управляющие решения. Таким образом, неизвестное управляющее решение выражается набором нечетких значений, задающих насколько применимо в текущей ситуации каждое из стандартных решений.

Степени предпочтения управляющих решений определяют эксперты. Если степени предпочтения зависят от ситуации, то они могут быть определены при помощи системы «ситуация – предпочтение решений» (С-ПР), представляющей собой базу знаний. В такой базе знаний нечетким эталонным ситуациям соответствуют (с заданной степенью) управляющие решения. Поиск степени управляющего решения в конкретной ситуации происходит путем ее сравнения с эталонными ситуациями. В качестве искомой выбирается степень решения для ситуации, наиболее близкой к рассматриваемой.

Построение нечеткой ситуационной сети для объекта физической защиты

Если рассматривать объект физической защиты как объект управления НСС, то элементы сети будут следующими. Ситуации – это возможные состояния объекта с точки зрения его уровня защищенности от действий возможного нарушителя. Состояние объекта описывается набором его свойств. Объект представляется множеством точек контроля, следовательно ситуация будет описываться свойствами точек контроля. Для описания ситуации используются лингвистические переменные вида «Уровень возможностей имеющихся средств защиты». Рассматриваемые средства защиты должны включать в себя естественную защищенность точки контроля (структура помещения, прочность стен, дверей, окон), так же как и существующие элементы СФЗ. Например:

• У ВО₁ – Уровень возможностей имеющихся средств защиты по обнаружению нарушителя в точке контроля 1;

• У ВЗ₁ – Уровень возможностей имеющихся средств защиты по затруднению перемещения нарушителя в точке контроля 1;

• У ВП₁ – Уровень возможностей имеющихся средств защиты по ограничению доступа в точку контроля 1;

• У ВР₁ – Уровень возможностей имеющейся системы телевизионного наблюдения по распознаванию объектов в точке контроля 1;

• УВО₂ – Уровень возможностей имеющихся средств защиты по обнаружению нарушителя в точке контроля 2 и т.п.

Нечеткая ситуация, определяющая состояние объекта, содержит набор лингвистических переменных, где для каждой переменной определяется степень принадлежности всем ее возможным значениям, или термам, например:

{« 0,1 /"Значение 1">, <0,8/" ЗначениеЗ">, < 0,4/" ЗначениеЗ" > /" УВО1" >,

« 0,1/"Значение1" >, < 0,6/" ЗначениеЗ" >, < 1/" ЗначениеЗ" >/" УВ31" >,

« О,3/"3начение1" >, < 0,6/" ЗначениеЗ" >, < 0,1/" ЗначениеЗ" > /" УВП," >,

« 0,4/"Значение1" >, < 0,5/" ЗначениеЗ" >, < 0/" ЗначениеЗ" >/" УВР1" >,

« 0,1 /"Значение 1">, <0,8/" ЗначениеЗ">, < 0,4/" ЗначениеЗ" > /" УВО2" >,...}.

Важной задачей при описании нечетких ситуаций также является выбор типов функций принадлежности термов.

Исходная ситуация – это текущее состояние объекта защиты. Целевая ситуация – это объект, обладающий требуемым уровнем защищенности. Управляющие решения – это указания по необходимым изменениям защищенности объекта для достижения требуемого уровня. Возможные управляющие решения – это лингвистические переменные вида: «Увеличить», «Уменьшить», «Не изменять», задающие уровень необходимых изменений для каждого свойства объекта защиты.

Приведем пример построения по обратному методу НСС для объекта физической защиты. В качестве объекта защиты выбран нефтеперерабатывающий завод. Множество защищаемых зон объекта или точек контроля: y1 – база товарно-материальных ценностей, y2 – коммерческий узел учета нефти, y3 – технологическая установка, y4 – цех товарно-сырьевого производства, y5 – водозабор, y6 – биологические очистные сооружения.

В условном примере для описания ситуаций будем использовать свойства только одной точки контроля, например базы товарно-материальных ценностей. Точка контроля характеризуется четырьмя свойствами. Каждая лингвистическая переменная, описывающая свойство, имеет свой набор термов – T и базовое множество – D:

{УВО, Tо, Dо} – Уровень возможностей имеющихся средств защиты по обнаружению нарушителя;

{УВЗ, Tз, Dз} – Уровень возможностей имеющихся средств защиты по затруднению перемещения нарушителя;

{УВП, Tп, Dп} – Уровень возможностей имеющихся средств защиты по ограничению доступа;

{УВР, Tр, Dр} – Уровень возможностей имеющейся системы телевизионного наблюдения (СТН) по распознаванию объектов.

Используем термы: «низкий» – Н; «средний» – С; «высокий» – В.

Терм-множества признаков: Tо = {Но, Со, Во}, Tз = {Нз, Сз, Вз}, Tп = {Нп, Сп, Вп}, Tр = {Нр, Ср, Вр}. Базовые множества всех термов D1 = D2 = D3 = [0, 1], так как термы определяются вероятностями выполнения средствами защиты своих функций (противодействия возможным угрозам).

Эти вероятности должны быть известны для каждого терма всех свойств. Экспертам необходимо сопоставить (четкие или нечеткие) числовые значения вероятностей термам вида «низкий», «средний», «высокий». Например, в случае если известно четкое значение вероятности распознавания объектов для СТН, то высокий уровень будет соответствовать 0,95; средний 0,80; низкий 0,50.

Пример эталонных ситуаций для НСС объекта защиты:

s, = {«0,1/"Но">, <0,8/"Co">, <0,4/"Bo"> / "УВО">, «0,1/"Нз">, <0,6/"Сз">, <0,1/"Вз"> / "УВЗ">, «0,3/"Нп">, <0,6/"Сп">, <0,2/"Вп"> / "УВП">, «0,7/"Нр">, <0,3/"Ср">, <0,1/"Вр"> / "УВР">};

s2 - {«0,1/"Но">, <0,8/"Со">, <0,4/"Во"> / "УВО">, «0,1/"Нз">, <0,6/"Сз">, <0,1/"Вз"> / "УВЗ">, «0,3/"Нп">, <О,б/"Сп">, <0,2/"Вп"> / "УВП">, «0,2/"Нр">, <0,7/"Ср">, <0,3/"Вр"> / "УВР">} ...;

sn = {«0,1/"Но">, <0,3/"Со">, <0,8/"Во"> / "УВО">, «0,1/"Нз">, <0,2/"Сз">, <0,9/"Вз"> / "УВЗ">, «0,2/"Нп">, <0,4/"Сп">, <0,7/"Вп"> / "УВП">, «0,1/"Нр">, <0,3/"Ср">, <0,7/"Вр"> / "УВР">}.

Управляющие решения задаем лингвистическими переменными:

«Увеличить» – {I, TI, XI}, «Уменьшить» – {D, TD, XD}, «Не изменять» – {Z, TZ, XZ}.

Увеличение или уменьшение могут проводиться с различной силой воздействия, то есть иметь несколько уровней, например «немного» и «сильно».

В примере используем три уровня: «немного», «средне» и «сильно», соответственно терм-множества лингвистических переменных будут следующие:

TI = {Tlb ТЬ, Tl3}, TD = {TDb TDb TD3}, TZ = {TZ}, где термы: TI1 – «немного увеличить», TI2 – «средне увеличить», TI3 – «сильно увеличить», TD1 – «немного уменьшить», TD2 – «средне уменьшить», TD3 – «сильно уменьшить», TZ – «не изменять».

Примеры матриц отношений, описывающих управляющие решения по признаку УВО, приведены на рис. 1.

	термы	и	с	в
	н	0,3	0,8	0
Мтп	с	0	0,4	0,6
	в	0	0	1
	термы	н	С	в
	н	0	1	0,3
	с	0	0,1	1
	в	0	0	1
	термы	н	с	в
	н	1	0	0
	с	0	1	0
	в	0	0	1

Рис. 1. Матрицы управляющих решений по признаку УВО

Теперь необходимо определить управляющие решения для перехода между ситуациями и степени предпочтения применения этих решений. Определим управляющее решение R1 для перехода от ситуации s1 к ситуации s2. Для этого нужно получить декартово произведение значений признака УВР в ситуациях s1 и s2, так как только по этому признаку отличаются ситуации s1 и s2:

Si - « 0,7/"Hp" >, < 0,3/"Cp" >, < 0,l/"Bp" > / "УВР" >;

s2 - « 0,2/"Hp" >, < 0,7/"Cp" >, < 0,3/"Bp" > / "УВР" >.

Матрица произведения отображена в таблице 1. Далее необходимо определить нечеткое множество Ri = {, < pRi(TI2)/TI2 >

,,

^<Pri(TDi)/TDi>,

Ri(TD₂)/TD₂>,

, }.

Таблица 1. Декартово произведение значений признака УВР в ситуациях s1 и s2

термы	Нр	Ср	Вр
Нр	0,2	0,7	0,3
Ср	0,2	0,3	0,3
Вр	0,1	0,1	од

Для определения коэффициентов вычислим степени включения отношения R1 в отношения TI1, TI2, TI3, TD1, TD2, TD3, TZ, описанные матрицами:

Pri(TII) = v(M_RbM_TII);

Pri(TI2) = v(M_RbM_T]2);

Pri(TI3) = v(MRi,Mti3);

Pri(TDI) = v(MRi,Mtdi);

Pri(TD2) = v(M_RbM_TD2);

Pri(TD3) = v(M_R],M_TD₃);

Pri(TZ) = v(M_RbM_TZ).

Степень включения нечеткого множества А в нечеткое множество В находится по формуле: v(A, В)= & (Цд(х) —> Цв(х)); х С X, при этом Ца(х) ^ Цв(х) = max (1- Ца(х), Цв(х)).

Полученное нечеткое множество: R1 = {<0,7/ TI1>, <0,7/TI2>, <0,5/TI3>, <0,3/TD1>, <0,3/TD2>, <0,3/TD3>, <0,3/TZ1>}. Для перехода от s1 к s2 необходимо применять стандартное управляющее решение, имеющее наибольшую степень принадлежности нечеткому решению R1. Этим реше- нием является TI1 или TI2, то есть небольшое или среднее увеличение.

Для получения степени α(s1, R1) предпочтения применения решения R1 в ситуации s1 нужно обратиться к системе С-ПР. Пусть степень равна 0,7. Отмечаем дугу (s1, s2) графа общности ситуаций решением R1 со степенью предпочтения 0,7. Аналогично обработав все пары ситуаций, имеющих общность по признакам, получим НСС, характеризующую динамику перехода объекта из ситуации в ситуацию (см. рис. 2).

Готовая НСС используется для определения последовательности действий или пути перехода между любой исходной и целевой ситуацией, причем этот процесс может быть полностью автоматизирован.

Поиск стратегии управления методом сжатия нечеткой ситуационной сети

В модели «ситуация – стратегия управления – действие» (С-СУ-Д) для поиска стратегии управления требуется готовая НСС. Стратегия управления описывается оптимальным маршрутом по НСС между текущей нечеткой ситуацией si Є S и целевой ситуацией sc Є S. В качестве критерия оптимальности может использоваться, например, средний вес пути - отношение суммы степеней предпочтения входящих в него дуг к количеству этих дуг, или прочность пути - минимум степеней предпочтения дуг пути, или длина пути - количество дуг.

Общее количество ситуаций и переходов между ними в НСС, описывающих реальные объекты, может быть очень большим. Для упрощения задачи поиска стратегии управления используют методы сжатия НСС. Приведем описание метода сжатия НСС для объектов, обладающих взаимной независимостью значений признаков. Зададим нечеткое отношение (p – 1)-общности = (S, F), где

Hf (Si, sj) = ■<

kp_i (st, sj), если kp.i (s15 Sj) > t;

О, если kp., (Sj, Sj) < t.

Данное отношение соответствует нечеткому графу G т = (S, F), который отличается от графа НСС тем, что в графе G т дуги (s_i, s_j) нагружаются степенью k_p-1 (s_i, s_j), определяющей (p – 1) - общность ситуаций s_i и s_j.

Отношение τ = (S, F) является отношением нечеткой толерантности, так как оно нечетко рефлексивно и нечетко симметрично (любая ситуация имеет общность сама с собой, и из общности ситуаций s₁ и s₂ следует общность s₂ и s₁). Наличие толерантности отношения τ позволяет определить нечеткое покрытие множества вершин графа G t* Классы покрытия R вершин графа G т по отношению τ являются «структурами общности». Структуре общности A_i Є R графа G т принадлежат вершины s₁ⁱ, s₂ⁱ, …, s_giⁱ (g_i ≤ n) такие, что для каждых двух вершин (s_mi, s_ki) (m, k Є N = {1,

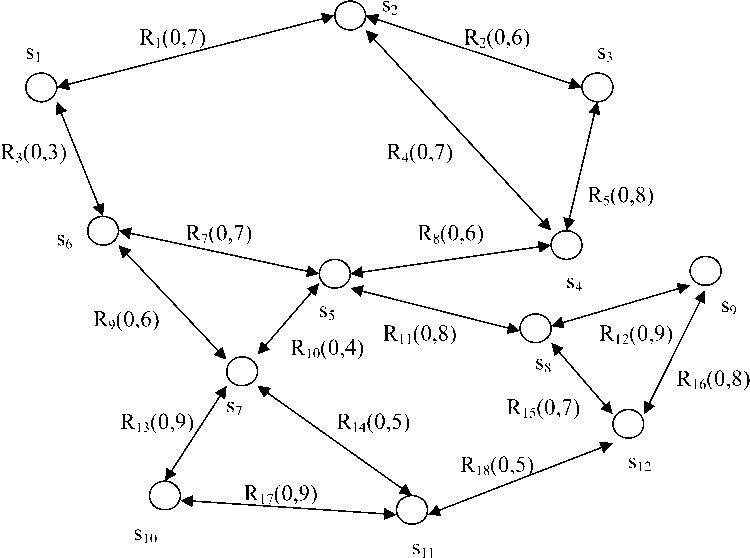
Рис. 2. Пример HCC объекта физической защиты

• 2,    ..., g_i}) возможен переход из s_mⁱ в s_kⁱ и наоборот через применение одного однолокального управляющего решения. Структуры общности, имеющие непустые пересечения друг с другом, называются соседними, а множество вершин области пересечения двух соседних структур называются областью перехода структур общности [4].

Нечеткий путь между вершинами si и sj обозначается L (si, sj) и содержит вершины s Є S и степени принадлежности μF, образуя последовательность вида: si – μF (si, sj) – sj – μF (sj, sp) – sp ... sx – μF (sx, sk) – sk. В качестве критерия оптимальности в условном примере используем длину пути. Путь, имеющий наименьшую длину (число ребер), считается кратчайшим. Если несколько путей между одной и той же парой вершин имеют наименьшую длину, оба пути будут кратчайшими.

Если вершины s_m, s_n Є S (s_m ≠ s_n) принадлежат соседним структурам общности A_i и А_j, то длина кратчайшего пути между вершинами s_m и s_n не превышает 2. Следовательно, можно из любой вершины одной структуры общности перейти в любую вершину соседней структуры общности, применяя не более двух однолокальных управляющих решений. При этом одна из вершин области перехода структур A_i и A_j будет использоваться в качестве промежуточной для пути из s_m в s_n и наоборот. В том случае если структуры общности A_i и A_j не соседние, то для определения пути надо использовать такую кратчайшую последовательность структур общности, в которой каждая последующая структура – соседняя предыдущей. Для нахождения этой кратчайшей последовательности необходимо построить граф концентрации структур общности графа G т? задаваемый следующим определением:

Граф G' = (R, P) называется графом концентрации структур общности нечеткого графа = (S, F), если R = {A1, A2, …, An} принято в качестве множества вершин и P = {p = (Ai, Аj)}, Ai ∩ Аj ≠ Ø, (Ai, Аj) Є R2. [4]

В итоге для поиска стратегии управления по готовой НСС при условии взаимной независимости значений признаков объекта можно использовать следующие этапы решения.

• 1.    Построить нечеткий граф G т = (S, F).

• 2.    Построить структуры общности в G т.

• 3.    Перейти от G_T = (S, F) к графу концентрации структур общности G’ = (R, P).

• 4.    Определить множества M_i и M_c структур общности, которым принадлежат s_i и s_c.

• 5.    Если M_i ∩ M_c ≠ Ø, то из s_i можно перейти в s_c , применяя не более одного однолокального управления.

• 6.    Если (A_k Є M_i) ( A_j Є M_c) (A_k ≠ A_j) (A_k ∩ А_j ≠ Ø), то поставить одну из вершин области перехода структур A_k и A_j в качестве подцели между s_i и s c .

• 7.    Если ( A_k Є M_i) ( A_j Є M_c) (A_k ∩ А_j = Ø), то определить путь L – имеющий наименьшее число ребер среди всех путей между всевозможными парами структур общности A_k Є M_i и A_j Є M_c; в графе G' – и указать последовательность точек переходов (или вершин из областей переходов) соседних структур общности, входящих в L, в качестве стратегии управления для перехода из s_i в s_c [4].

Рассмотрим пример сжатия НСС для объекта физической защиты. Нечеткий граф объекта G т = (X', F) изображен на рис. 3. Определим в графе структуры общности:

Ai = {<0,8/si>, <0,8/s2>};

A2 = {<0,5/s2>, <0,6/s3>, <0,5/s4>};

A3 = {, };

A4 = {<0,6/si>, <0,6/s6>};

A5 = {<0,7/s5>, <0,5/s6>, <0,5/s7>};

Аб = {<0,6/s5>, <0,6/s8>};

Ay = {<0,8/s8>, <0,7/sg>, <0,7/si2>};

A8 = {<0,8/s7>, <0,6/siq>, <0,6/sn>};

Ag = {<0,9/sn>, <0,9/si2>}.

Полученный граф G' = (R, P) концентрации структур общности графа G т изображен на рис. 4.

Определим стратегию управления по переводу объекта физической защиты, например, из нечеткой ситуации s2 в нечеткую ситуацию s9. Обращаясь к процедуре построения стратегий управления, определяем множества M2 и M9 структур общности, которым принадлежат соответственно s2 и s9: M2 = {A1, A2), M9 = {A7}. Так как M2 ∩ M9 = Ø, то из s2 нельзя перейти в s9, применяя однолокальное управляющее решение. Так как не имеется ни одной пары вершин, смежных между собой, из числа принадлежащих M2 и M9, то переходим к поиску кратчайшего из всех возможных путей в графе G' между всеми парами вершин множеств M2 и M9. Кратчайший путь L = (A2, A3, A6, A7). Переходя к точкам перехода соседних структур общности пути L, получаем стратегию управления: C(s2, s9) = (s2, s4, s5, s8, s9). Искомый путь на рис. 3 и рис. 4 выделен двойной линией.

Таким образом, согласно полученной стратегии управления, кратчайшим путем для перевода объекта физической защиты из нечеткой ситуации s2 в нечеткую ситуацию s9 является путь s2, s4,

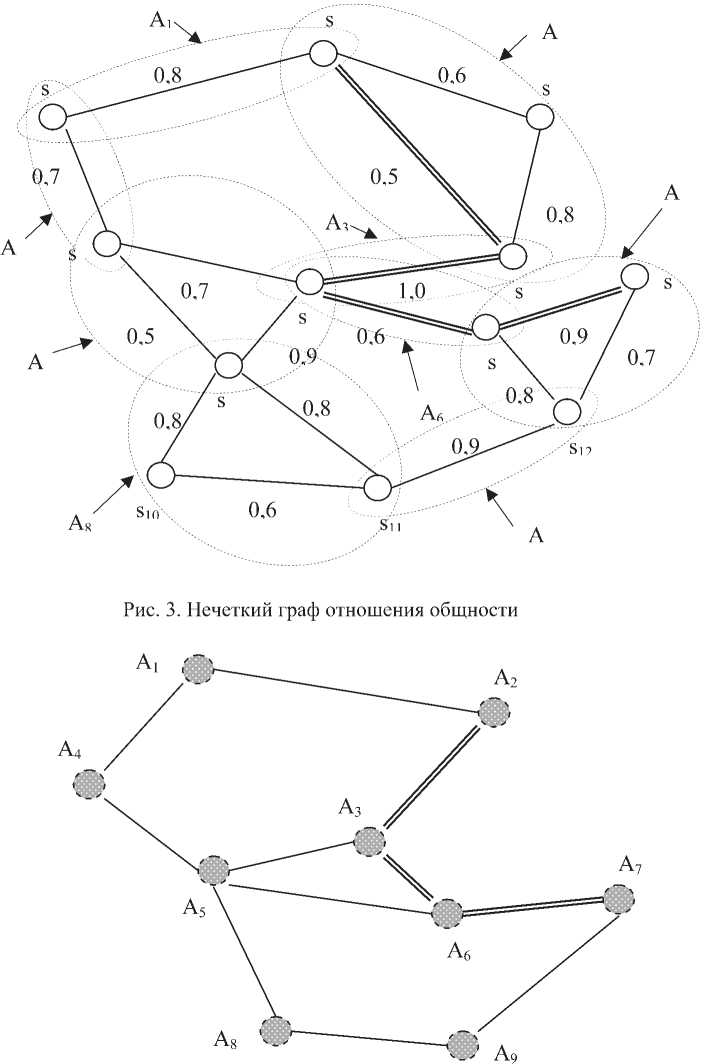
Рис. 4. Граф структур общности

• s₅,    s₈, s₉. Для осуществления перевода необходимо последовательно применить однолокальные управляющие решения: R₄, R₈, R₁₁, R₁₂. Так как каждое однолокальное решение в НСС задается уровнем изменения одного признака, то последовательность решений может означать, например, следующие действия:

• -    немного увеличить УВР,

• -    средне увеличить УВЗ,

• -    немного уменьшить УВО,

• -    сильно увеличить УВП.

Заключение

Представленный способ поиска стратегии управления по нечеткой ситуационной сети для определения действий по корректировке состава СФЗ объекта обладает следующими достоинствами.

• 1.    Процесс принятия решения по НСС может быть полностью автоматизирован, экспертные знания используются только в процессе построения НСС.

• 2.    Для одного объекта необходимо построить только одну НСС, которая будет использоваться для поиска стратегии управления любое число раз для любых возможных исходных и целевых ситуаций.

К недостаткам использования нечеткой ситуационной сети можно отнести следующее. Для адекватного отражения действительности при работе с реальными объектами число признаков ситуаций и количество самих ситуаций должно быть очень велико. Соответственно, потребуются большие размеры НСС и возрастет трудоемкость ее построения. Таким образом, применение модели С-СУ-Д в процессе проектирования СФЗ объекта может повысить эффективность принятия решений при модернизации СФЗ.