Природа массы, сил инерции, тяжести и центробежной силы, математическое обоснование принципа маха

Введение. «… Природа массы - вопрос №1 современной физики» -отметил академик Л.Б. Окунь [1]. В 1896 году австрийский физик Эрнст Мах высказал гипотезу, что масса тела определяется гравитационным влиянием всех объектов Вселенной, которая вошла в историю физики как принцип Маха. Мах не смог математически доказать правильность своей гипотезы. Несмотря на это: «…Принцип Маха продолжает широко привлекаться в теоретических работах, ставящих целью выяснение строения и свойств Вселенной в целом» [2].

Опираясь на законы природы, описанные во всех учебниках физики для средней школы, приводим    исправленное и дополненное доказательство принципа Маха [4].

Математическое обоснование принципа Маха.

Формирование силы гравитационного взаимодействия. Будем рассматривать Вселенную, как совокупность бесконечно большого числа локальных точечных объектов, расположенных по одну и другую стороны от пробного тела, представляющей два полупространства, разделённых гипотетической плоскостью А-А, проходящей через точку наблюдения (рис.1), рассматривая «бесконечность» как, неизмеримо большую физическую величину, стремящуюся к бесконечности.

Сила взаимодействия пробного тела с точечным объектом Вселенной определяется по закону всемирного тяготения:

F„ = G

m Mn

Rn

где: F« - сила взаимодействия тела и n -ого точечного объекта

Вселенной;

G - гравитационная постоянная, m - масса пробного тела;

M n - масса n -ого локального объекта Вселенной;

R n - расстояние до n -ого объекта Вселенной.

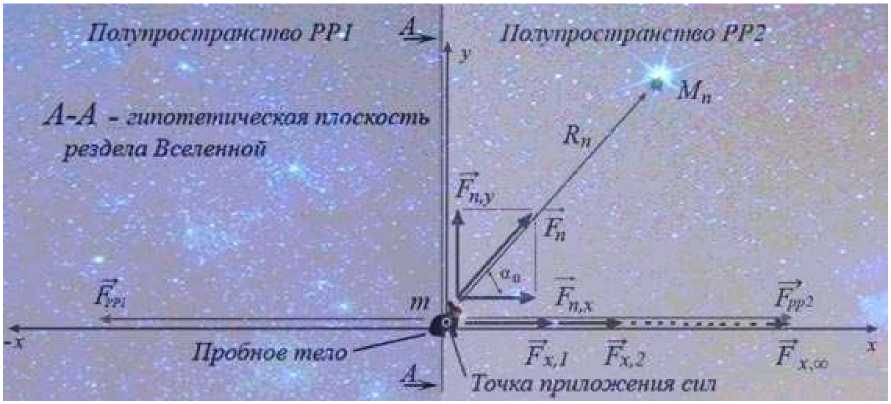
Рис.1. Схема гравитационного взаимодействия пробного тела и

массы Вселенной .

В формировании силы притяжения пробного тела к полупространству участвует проекция вектора силы на ось Х:

Гп,х- v “ — cose.

Учитывая принцип суперпозиции полей, сила гравитационного взаимодействия пробного тела с одним полупространством, равна сумме сил взаимодействия с локальными объектами:

Ppp- ”^"Рпд⁼Р1д* Ргд*......⁺ Кд ,                 (3)

где:     - сила гравитационного взаимодействия пробного тела с полупространством РР2. Аналогично формируется F" - сила гравитационного взаимодействия тела с полупространством РР1. Вес тела, относительно полупространств, при отсутствии влияния близко расположенных локальных объектов, равен силе гравитационного притяжения:

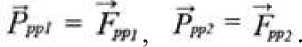
Суммарное гравитационное поле Вселенной будет равно:

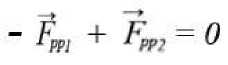
или

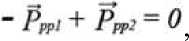
где:          , *'•  - вес тела, относительно полупространств.

Взаимодействие массы Вселенной и пробного тела (Рис.2) .

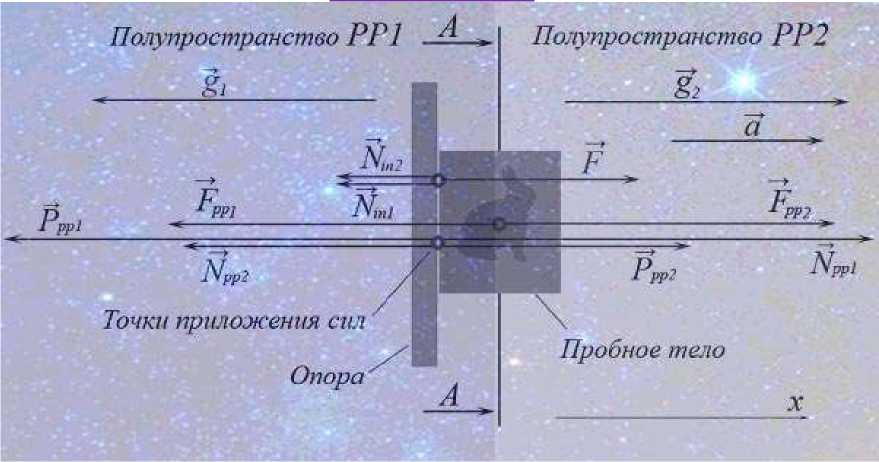
Рис.2. Схема формирования сил гравитационного взаимодействия массы Вселенной и пробного тела, движущегося с ускорением.

По второму закону Ньютона:

• -    Силы притяжения полупространств, создают ускорения свободного падения:

  -          o₁₌S^L А ₌ ‘РР2 А ₌

или           ,               или             (7)

Вес тела, действуя на опору, согласно третьему закону Ньютона, создаёт силы нормальной реакции опоры:

=      ;         =      .                         (8)

Соответственно, возникают силы     реакции тела на опору, противодействующие ускоренному перемещению тела относительно полупространств.     Равнодействующая     сила           является противодействием силе / , и воспринимается как сила инерции:

+      =                               (9)

• -     =   .                                     (10)

Ускорение свободного падения тела, на      соответствующее полупространство, при ускоренном движении изменится на величину ускорения движения тела. Модуль веса тела принимает значение:

• -    от которого удаляется

Pppi = m(g, + a) = mgj + ma       (11а)

• -    к которому приближается

Ppp2 = m(g2 - a) = mg2 - ma       (11б)

Подставляя значения из (7), (8), (10), получаем вес тела относительно полупространств при ускоренном движении:

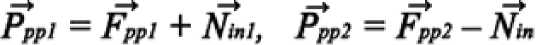
В результате ускоренного движения, вес тела, относительно каждого полупространства,  изменится на величину силы противодействия перемещению, которая воспринимается как инерционная:

Ppp! — Ppp2 = Fppl + Nin! — (Fpp2 — Nini) Ppp! — Ppp2 = Nin! + Nin2

учитывая равенство (9):

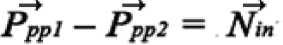
По второму закону Ньютона:

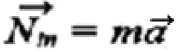
или

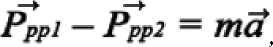
отсюда:

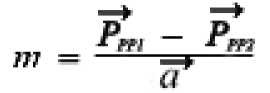
или

Т.е., масса тела равна разности гравитационного притяжения полупространств Вселенной, относительно которых тело ускоренно движется.

Экспериментальные факты

Факт 1. Тело с массой m , двигаясь по окружности с радиусом Г ,

V2

под действием центростремительной силы "■    1    , получает

Я = т ускорение:   '     ?' .

Относительно полупространств Вселенной, в соответствии со вторым законом Ньютона ускорение тела принимает значение:

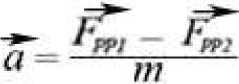
или

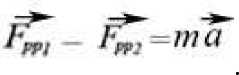
Отсюда:

• -    силы действующие на тело:

• - *- "^ ^      "^     "^

• - '^  ^^Т^."   , или -'^  ^;^'^А:-.

Центростремительная сила и сила взаимодействия тела с полупространствами Вселенной автоматически уравниваются. Сила гравитационного взаимодействия тела с массой Вселенной проявляется как центробежная. В результате, чем больше скорость вращения, тем больше ускорение и, соответственно, больше центробежная сила. Итак, до бесконечности. Это подтверждается экспериментально на центрифуге, -насколько позволяют её технические возможности.

Факт 2. Ньютон, создав теорию тяготения, не смог объяснить причину устойчивости планет на орбите. Планеты находятся под действием центростремительной силы, которая обратно пропорциональна квадрату расстояния, а центробежная сила обратно пропорциональна первой степени расстояния, что приводит, по его теории, к неустойчивому равновесию планеты на орбите. Любое незначительное отклонение планеты, должно нарушить равновесие сил. Ньютон, понимая это противоречие, отметил: « … поддержание настоящего вида Солнечной системы     требует     вмешательства     каких-то     посторонних сверхъестественных сил» [5]. Астрофизики объясняют устойчивость космических тел на орбите: «… Только учёт формальных законов сохранения (энергии, импульса и момента импульса) позволяет в рамках механики решить эту проблему, да и то, лишь в ограниченном числе простых случаев. Но даже и в этих случаях физический механизм, стабилизирующий орбиты остаётся таинственным и непонятным» [5]. Принимая во внимание принцип Маха, и существование бесконечно большого поля в любой точке Вселенной, законы Ньютона позволяют объяснить природу центробежной силы, и устойчивость планет на орбите.

Несостоятельность критики принципа Маха

Эйнштейн отмечал: «… На тело должна действовать ускоряющая сила, когда соседние с ним массы подвергаются ускорению, причем ее направление должно совпадать с направлением этого ускорения … инертность некоторого тела должна возрасти, если поблизости от него сконцентрируются тяжелые массы» [3, с. 67]. Несостоятельность этого утверждения заключается в следующем:

• -    Отношение массы локального объекта к бесконечно большой массе

Вселенной в пределе стремится к бесконечно малой величине:

Lim f(m/M) = 0

(17) 16

M—too

, где: m – масса локального объекта Вселенной,

M

–

масса Вселенной.

Поэтому влияние локального объекта (локального скопления массы), сравнительно с бесконечно большим гравитационным полем Вселенной, также стремится к бесконечно малой величине, и выявить и измерить это влияние невозможно.

Заключение:

• -    Приведенное математическое обоснование доказывает принцип Маха как результат гравитационного влияния бесконечно большой массы Вселенной в любой точке пространства;

• -    Масса тела – это результат гравитационного взаимодействия тела и бесконечно большой массы Вселенной;

• -    Сила тяжести - это сила гравитационного взаимодействия тела с локальным объектом Вселенной (Земля, Луна и др.), нарушающего равновесие бесконечно больших гравитационных сил от полупространств Вселенной, создающего аномалию гравитационного поля;

• -    Сила инерции и сила тяжести имеют гравитационную природу - это объясняет их эквивалентность, поэтому различить их невозможно.